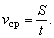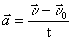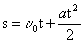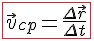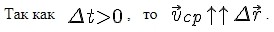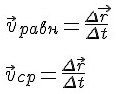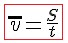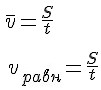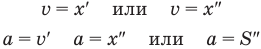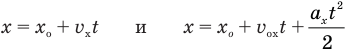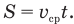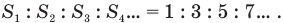Что такое переменное движение



то средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь:
Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, называется ускорение.
Мгновенное ускорение 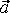
Равномерно-переменное движение — это движение, при котором за одинаковые промежутки времени скорость увеличивается или уменьшается на одинаковую величину.
Скорость равномерно-переменного движения выражается формулой v = v0 + at, (19)
где v—скорость равномерно-переменного движения в данный момент, м/сек;
Ускорением называется изменение скорости в единицу времени.
Ускорение а имеет размерность скорость / время = м / сек 2 и выражается формулой a = (v-v0)/t. (20)
Путь, пройденный при равномерно-переменном движении, выражается формулой S= ((v0+v)/2)* t = v0t+(at 2 )/2. (21)
авномерное движение точки по окружности— движение точки с постоянной по модулю скоростью (v=const) по траектории, представляющей собой окружность. Но, т.к. скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит равномерное движение по окружности – ускоренное движение! Точка совершает перемещение с постоянной по модулю скоростью, следовательно: 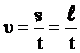
мВремя, за которое тело совершает один оборот, т.е. поворачивается на угол 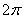
Частотой обращения называется число оборотов по окружности в единицу времени.
Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:
Что такое переменное движение
§ 17. Переменное движение. Средняя скорость. Средний модуль скорости
1. Переменное движение.
2. Средняя скорость.
Определение 2а. Средней скоростью переменного движения называется отношение перемещения ко времени, за которое это перемещение произошло.
Запишем формулу скорости равномерного движения и средней скорости переменного движения.
Если посмотреть на правые части этих равенств, заметим, что они одинаковы. В этом заключается смысл средней скорости.
Определение 2б. Под средней скоростью переменного движения понимают скорость некоторого воображаемого равномерного прямолинейного движения, у которого перемещение и время одинаковы с переменным движением.
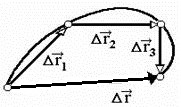
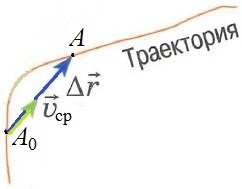
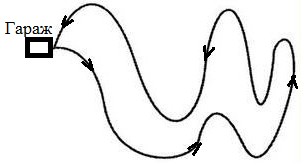
Согласно рисунку, представленному выше, это понимать надо так. Если бы точка двигалась не переменно по криволинейной траектории, а равномерно и прямолинейно прямо по вектору перемещения 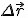
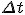
Модуль вектора средней скорости, или модуль средней скорости :
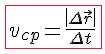
3. Средний модуль скорости.
На практике при составлении расписания движения поездов, автобусов используют ещё одно понятие средней скорости, которое называют средним модулем скорости, то есть средним по времени модулем всех скоростей, которые имела точка на различных участках траектории.
Определение 3а. Средним модулем скорости переменного движения называется отношение пути S ко времени t, за которое этот путь пройден.
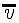
Не надо путать средний модуль скорости с модулем вектора средней скорости.
Например, если автобус вышел на маршрут в начале дня и к концу дня возвратился в гараж, то перемещение за всё время движения равно нулю 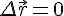
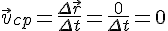
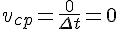
Но средний модуль скорости отличен от нуля, так как не равен нулю путь, пройденный автобусом:
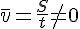
Аналогично для бумеранга.
За время полёта бумеранга средняя скорость его движения и модуль средней скорости равны нулю, так как равно нулю перемещение бумеранга относительно точки А (см. рис.). Но так как путь, который проделал бумеранг, не равен нулю, то и средний модуль скорости движения бумеранга отличен от нуля.
Если посмотреть на правые части формул модуля скорости равномерного движения и среднего модуля скорости переменного движения, то увидим, что правые части равенств одинаковы.
В этом заключается смысл среднего модуля скорости.
Определение 3б. Средний модуль скорости переменного движения равен модулю скорости такого воображаемого равномерного прямолинейного движения, у которого путь и время одинаковы с переменным движением.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
Переменное движение
Смотреть что такое «Переменное движение» в других словарях:
переменное движение — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN variable motion … Справочник технического переводчика
переменное движение — kintamasis judėjimas statusas T sritis fizika atitikmenys: angl. variable motion vok. veränderliche Bewegung, f rus. переменное движение, n pranc. mouvement variable, m … Fizikos terminų žodynas
равномерно-переменное движение — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN uniform variable motion … Справочник технического переводчика
Механика — наука о движении. Изучая движение, механика необходимо должна изучать и причины, производящие и изменяющие движения, называемые силами; силы же могут и уравновешивать друг друга, и равновесие может быть рассматриваемо как частный случай движения … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Механика — наука о движении. Изучая движение, механика необходимодолжна изучать и причины, производящие и изменяющие движения, называемыесилами; силы же могут и уравновешивать друг друга, и равновесие можетбыть рассматриваемо как частный случай движения.… … Энциклопедия Брокгауза и Ефрона
Железо — (Ferrum) Металл железо, свойства металла, получение и применение Информация о металле железо, физические и химические свойства металла, добыча и применение железа Содержание Содержание Определение термина Этимология История железа Происхождение… … Энциклопедия инвестора
Листовое железо и сталь — Посредством прокатки в гладких вальках стальных и железных болванок получаются листы этих металлов различных размеров; по толщине их подразделяют: на кровельное самый тонкий сорт железа от 0,33 до 0,66 мм, сковородное или лопаточное несколько… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
kintamasis judėjimas — statusas T sritis fizika atitikmenys: angl. variable motion vok. veränderliche Bewegung, f rus. переменное движение, n pranc. mouvement variable, m … Fizikos terminų žodynas
mouvement variable — kintamasis judėjimas statusas T sritis fizika atitikmenys: angl. variable motion vok. veränderliche Bewegung, f rus. переменное движение, n pranc. mouvement variable, m … Fizikos terminų žodynas
variable motion — kintamasis judėjimas statusas T sritis fizika atitikmenys: angl. variable motion vok. veränderliche Bewegung, f rus. переменное движение, n pranc. mouvement variable, m … Fizikos terminų žodynas
Движение с переменным ускорением
Движение с переменным ускорением
Здесь 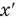
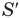
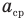
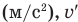
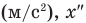
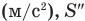
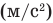
Правило сложения классических скоростей:
Здесь 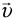
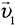
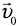
Если из условия задачи следует, что тело начало движение из состояния покоя, например, поезд отошел от станции или автомобиль выехал из пункта А и т. п., то в «Дано:» следует записать, что его начальная скорость 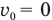
Из сравнения уравнений
следует, что если координата тела х зависит от времени движения t в первой степени, то это равномерное движение, а если координата х зависит от времени 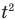
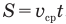
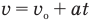
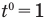
Если вам дано уравнение типа 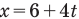
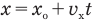
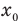
Если вам дано уравнение типа 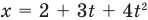
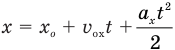
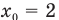
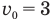
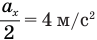
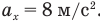
Формулу средней скорости 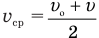
Пути, проходимые телом при равноускоренном движении без начальной скорости, относятся как ряд последовательных нечетных чисел:
Если в условии задачи идет речь о скорости в средней точке пути, то учтите, что это не средняя скорость на всем пути, а мгновенная скорость на середине пути, — она является конечной скоростью для первой половины пути и начальной скоростью для второй половины.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Равнопеременное движение
Рассмотрим прямолинейное движение тела вдоль оси (одномерный случай) и пусть при этом скорость тела изменяется.
Когда скорость изменяется, появляется ускорение. Ускорение, в свою очередь, тоже может меняться.
Если изменяется и ускорение, и скорость тела – движение сложное, например, колебательное;
Движение равнопеременное — если изменяется только скорость, а ускорение постоянное.
Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину.
При этом, если скорость увеличивается – движение называют равноускоренным, а если скорость уменьшается – равнозамедленным.
Примечание: Вместо слов «ускорение постоянное» можно произнести «ускорение не меняется», или «ускорение одно и то же».
Рекомендую предварительно ознакомиться с основными терминами для описания движения.
Будем выбирать направления для векторов скорости и ускорения относительно оси. Разберем несколько возможных вариантов.
Равноускоренное движение
Пусть при движении по прямой скорость тела увеличивается. Обратим внимание на перемещение тела.
Примечание: Движение равноускоренное, значит, за одинаковые интервалы времени перемещение будет увеличиваться на одну и ту же величину.
Этот факт иллюстрирует рисунок 1. Из рисунка видно: по сравнению с первой секундой, за вторую секунду пути перемещение увеличивается на небольшой отрезок, а за третью секунду – на два таких отрезка.
Считаем, что векторы скорости и ускорения сонаправлены с осью, вдоль которой движется тело (рис. 2).
Примечание: Скорость увеличивается, когда вектор ускорения сонаправлен с вектором скорости.
В начальный и в конечный моменты времени скорости будут различаться.
Формулы можно записать в скалярном виде, так как движение происходит вдоль одной прямой и направления векторов известны.
Связь между начальной и конечной скоростью выглядит так:
Уравнение движения выглядит так:
\[ S = v_ <0>\cdot t + a \cdot \frac
\[ x – x_ <0>= v_ <0>\cdot t + a \cdot \frac
Кроме уравнения движения теперь есть связь между скоростями. Поэтому, решая задачи, в которых скорость увеличивается, используем систему, состоящую из двух таких уравнений:
\[ \large \boxed < \begin
Примечание: Перемещение тела можно вычислить, не обладая информацией о времени движения, зная только начальную и конечную скорость тела и его ускорение. Об этом подробно написано в статье о формуле пути без времени.
Равнозамедленное движение
Пусть теперь тело движется по прямой и его скорость уменьшается. Рассмотрим перемещение тела.
Примечание: Движение равнозамедленное, значит, за одинаковые интервалы времени перемещение будет уменьшаться. При чем, на одну и ту же величину.
На рисунке 3 представлено изменение перемещения. Видно, что по сравнению с первой секундой, за вторую секунду перемещение уменьшается на небольшой отрезок, а за третью секунду – на два таких отрезка.
Примечание: Скорость будет уменьшаться, когда вектор ускорения направлен противоположно вектору скорости.
Пусть вектор скорости сонаправлен с осью, вдоль которой движется тело, а вектор ускорения – направлен против этой оси.
В начале и в конце пути скорости будут различаться.
Формулы можно записывать в скалярном виде, так как движение происходит вдоль одной прямой. Будем использовать знаки проекций векторов на ось.
Связь между скоростями выглядит так:
А уравнение движения имеет такой вид:
\[ S = v_ <0>\cdot t — a \cdot \frac
Заменив перемещение разностью конечной и начальной координат \( S = x — x_<0>\), получим:
\[ x – x_ <0>= v_ <0>\cdot t — a \cdot \frac
Значит, когда скорость уменьшается, для решения задач нужно использовать систему из двух таких уравнений:
\[ \large \boxed < \begin
Расшифруем теперь, к примеру, словосочетание «прямолинейное равнозамедленное движение» — это движение по прямой, ускорение есть, оно не меняется. Скорость тела уменьшается, так как вектор ускорения направлен противоположно вектору скорости.
Примечание: Перемещение замедляющегося тела можно вычислить не используя время. Потому, что существует запись формулы пути без времени для случая, когда скорость тела уменьшается.
Скорость направлена против оси, а ускорение – по оси
Дополнительно рассмотрим случай, когда скорость и ускорение направлены в противоположные стороны, ускорение – по оси, а скорость – против оси (рис. 5).
А если тело продолжит движение, то начнет двигаться в обратную сторону и модуль его скорости начнет увеличиваться. Поэтому, такое движение будет равноускоренным и будет сонаправленным с вектором ускорения.
Когда скорость направлена против оси, ее проекция на ось отрицательна и в уравнение она войдет со знаком минус. Ускорение же, напротив, совпадает с направлением оси, поэтому, войдет в уравнение со знаком «+».
Запишем связь между скоростями:
Уравнение движения для рассмотренного случая имеет такой вид:
\[ x – x_ <0>= — v_ <0>\cdot t + a \cdot \frac
Для выбранного направления векторов в итоге получим такую систему уравнений:
\[ \large \boxed < \begin
Решая задачи на движение, иногда вычисляют мгновенную и среднюю скорости.
Термины «мгновенная скорость» и «средняя скорость» применяют для случаев, когда скорость изменяется – то есть, для неравномерного движения.
Мгновенная скорость
Мгновенная скорость – это скорость тела в какое-то мгновение. Когда скорость тела меняется, то в различные мгновения (моменты времени) скорости будут различаться.
Мгновенную скорость v вычисляют, вместо символа t подставляя в формулу интересующее нас время:
Знак ускорения зависит его направления.
Средняя скорость
Средняя скорость тела – скорость, с которой нужно двигаться равномерно, чтобы пройти тот же путь за то же время.
Другими словами, средняя скорость помогает понять, с какой постоянной скоростью могло бы двигаться тело, чтобы пройти весь пройденный путь за такое же время.
Примечания:
Формула для расчета средней скорости:
\( S_<\text<весь>>(\text<м>) \) – полный путь, пройденный телом;
\( t_<\text<полное>> \left( c \right)\) – время, за которое тело прошло весь путь.