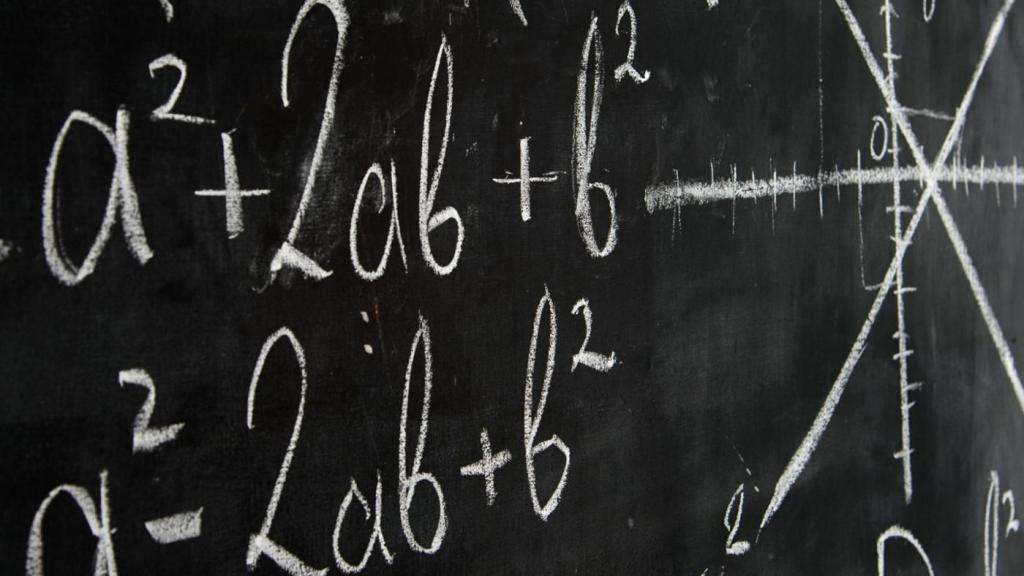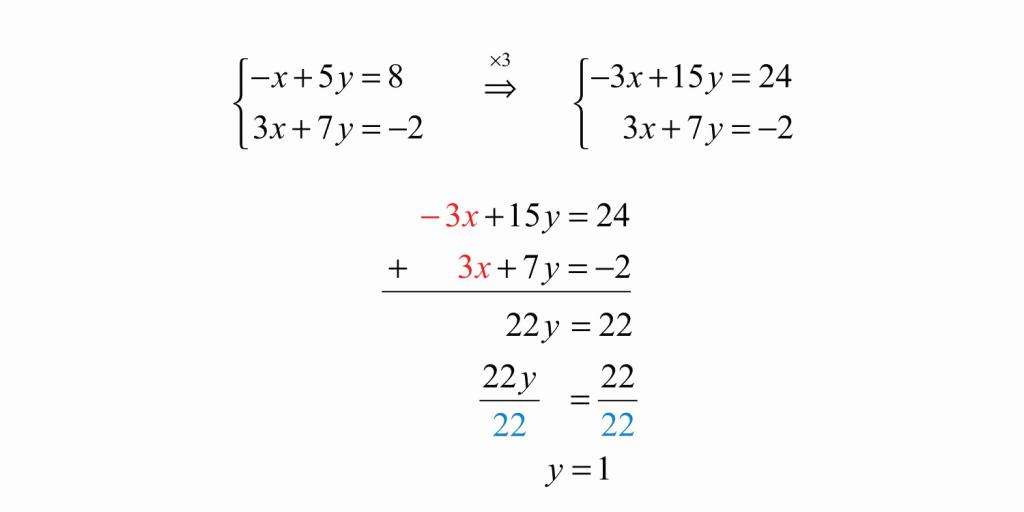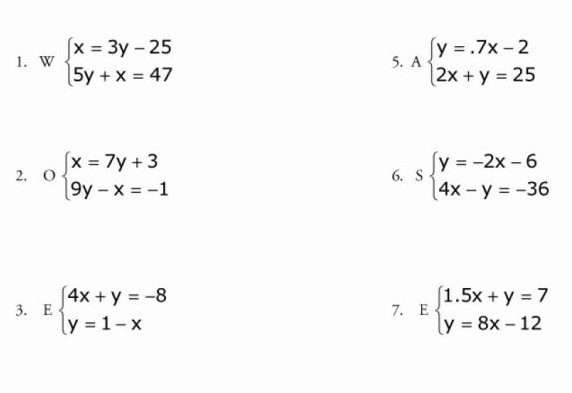Что такое переменные величины в математике 4 класс
Переменные и постоянные величины
Вы будете перенаправлены на Автор24
Переменные и постоянные величины – это не совсем просто
Школьная математика всегда убеждала и продолжает убеждать нас в том, что вопрос о переменных и постоянных величинах решается очень просто. Переменными считаются величины, которые в условиях данной задачи могут принимать различные значения. Постоянными считаются величины, которые в условиях данной задачи свои значения не меняют.
При этом дополнительно сообщается, что деление величин на переменные и постоянные достаточно условно и зависит от обстоятельств, сопровождающих процесс решения задачи. Одна и та же величина, которая в одних условиях считалась постоянной, в других условиях должна рассматриваться как переменная. Классический пример: сопротивление проводника считается постоянным, пока мы не оказываемся вынужденными учитывать зависимость величины его сопротивления от температуры окружающей среды.
Но, как показывает практика, всего вышеуказанного для корректного решения той или иной задачи бывает недостаточно.
Что такое величина, каждому ясно интуитивно. Уточним это понятие.
В общем случае содержанием процесса решения задачи есть преобразование величин. При этом следует понимать, что в общефилософском смысле величина, представляющая результат решения задачи, уже содержится в её формулировке в неявном виде. Нужно только правильно построить процесс преобразования величин задачи, чтобы этот результат представить явно.
Будем называть величиной любой математический объект, который несет (или может нести) информацию о том или ином значении.
Форма представления величин может быть различной. Например, величина с числовым значением, равным действительной единице, может быть представлена десятичной константой 1,0, функцией Cos(0), а также арифметическим выражением 25,0 – 15,0 – 9,0.
Значения величин можно менять. Так, в результате выполнения действия x = 1,0 величина в форме переменной x оказывается носителем значения действительной единицы. При этом предыдущее значение переменной x теряется. Приведённые примеры уже несколько с иных позиций показывают, что величины могут быть переменными и постоянными.
Готовые работы на аналогичную тему
Переменные величины обладают тем свойством, что их значения могут быть изменены в результате выполнения тех или иных действий. И это значит, что понятие “переменная величина” отражает возможность, но не факт изменения.
Постоянной величиной (константой) следует считать ту, значение которой, в отличие от переменной, изменить принципиально невозможно.
Например, значение постоянной величины в виде выражения 12+3 равно 15, и изменить его нельзя. При этом необходимо фиксировать смысл знаков, с помощью которых представляется величина. В противном случае, если считать, например, знаки этого выражения цифрами в системе счисления с основанием 5, то тогда его значение окажется равным 10.
Итак, в математических текстах носителями значений, то есть величинами, являются переменные, константы, обращения к функциям (или просто функции), а также выражения.
Особенности переменных
Обозначения, с которыми связываются определённые значения, в математике называют переменными (термин употребляется как имя существительное).
Например, значение переменной величины x+1 зависит от значения, связанного с обозначением x. Здесь обозначение x используется в качестве переменной. Изменив значение переменной x, мы тем самым изменим и значение переменной величины x+1.
Таким образом, значения переменных величин зависят от значений переменных, которые входят в их состав. Отличительным свойством переменной является то, что конкретное её значение должно быть ей просто приписано (назначено).
Математический подход, определяющий возможность вычисления значений переменных, в данном контексте оказывается неправильным. В математике можно вычислять только значения выражений.
Основное условие использования переменной в математических текстах в окончательном виде таково: для обращения к переменной достаточно указать её обозначение.
Особенности констант
В математических текстах могут быть использованы две разновидности констант: константы-лексемы и именованные константы.
Кстати, программисты на языках высокого уровня, пользуются этим на вполне формальных (законных) основаниях.
С помощью констант-лексем значения постоянных величин указываются непосредственно без выполнения каких-либо операций. Например, для получения значения постоянной величины 12+3, которая является выражением, необходимо выполнить сложение двух констант-лексем 12 и 3.
Именованная константа представляет собой обозначение, сопоставленное конкретному значению, указанному в виде константы-лексемы.
Помимо компактной записи выражений, именованные константы обеспечивают наглядность и значительные удобства в работе с математическими текстами.
Своё значение именованная константа приобретает как результат предварительной договорённости.
Важное свойство любой именованной константы состоит в том, что её значение не рекомендуется менять в пределах некоторого математического текста.
Выражения
Выражения являются составными частями подавляющего большинства математических текстов. С помощью выражений задают порядок вычисления новых значений на основании других заранее известных значений.
В общем случае в составе выражений используют операнды, знаки операций и регулирующие круглые (квадратные, фигурные) скобки.
Операнды – это общее название объектов, значения которых используют при выполнении операций. Операндами могут быть переменные, константы и функции. Кстати, этот термин весьма популярен в среде программистов. Фрагмент выражения, заключённый в регулирующие скобки, рассматривается как отдельный составной операнд.
Знак операции символизирует вполне определённую совокупность действий, которые должны быть выполнены над соответствующими операндами. Регулирующие скобки устанавливают нужный порядок выполнения операций, который может отличаться от предусмотренного приоритетом операций.
Простейшим случаем выражения является отдельный операнд. В таком выражении нет знаков операций.
Операнд-функция имеет свои особенности. Как правило, такой операнд представляет собой наименование (или знак) функции с последующим указанием в круглых скобках перечня её аргументов. В данном случае круглые скобки являются неотъемлемой принадлежностью функций и к регулирующим не относятся. Отметим, что во многих случаях в операндах-функциях обходятся без скобок (например, 5! – вычисление факториала целого числа 5).
Математические операции
Основные особенности математических операций таковы:
Таблица знаков некоторых операций и уровней приоритетов
Правила вычисления сложного выражения, содержащего цепочку операций при отсутствии регулирующих скобок, следующие:
При наличии регулирующих скобок выражение содержит составные операнды, значения которых должны быть вычислены в первую очередь.
Некоторые особенности записи математических выражений:
Что такое переменные? Переменная величина в математике
Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.
Понятие переменной

Виды величин

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).
Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.
История
История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.
Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.
С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:
За x2 принимаем некое k, и уравнение приобретает понятный вид:
Вот какую пользу в математику несет введение переменных.
Неравенства, примеры решения
Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:
Пример с одной переменной:
Делим обе части неравенства на 10 и получаем:
Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.
Решением этого неравенства будет промежуток (20; +∞).
Решение нестрогого неравенства осуществляется так же, как и строгого:
Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.
Квадратные неравенства
Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.
Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.
По формуле корней квадратного уравнения получаем:
Или можно было решить это уравнение по теореме Виета:
Методом подбора получаем такие же корни уравнения.
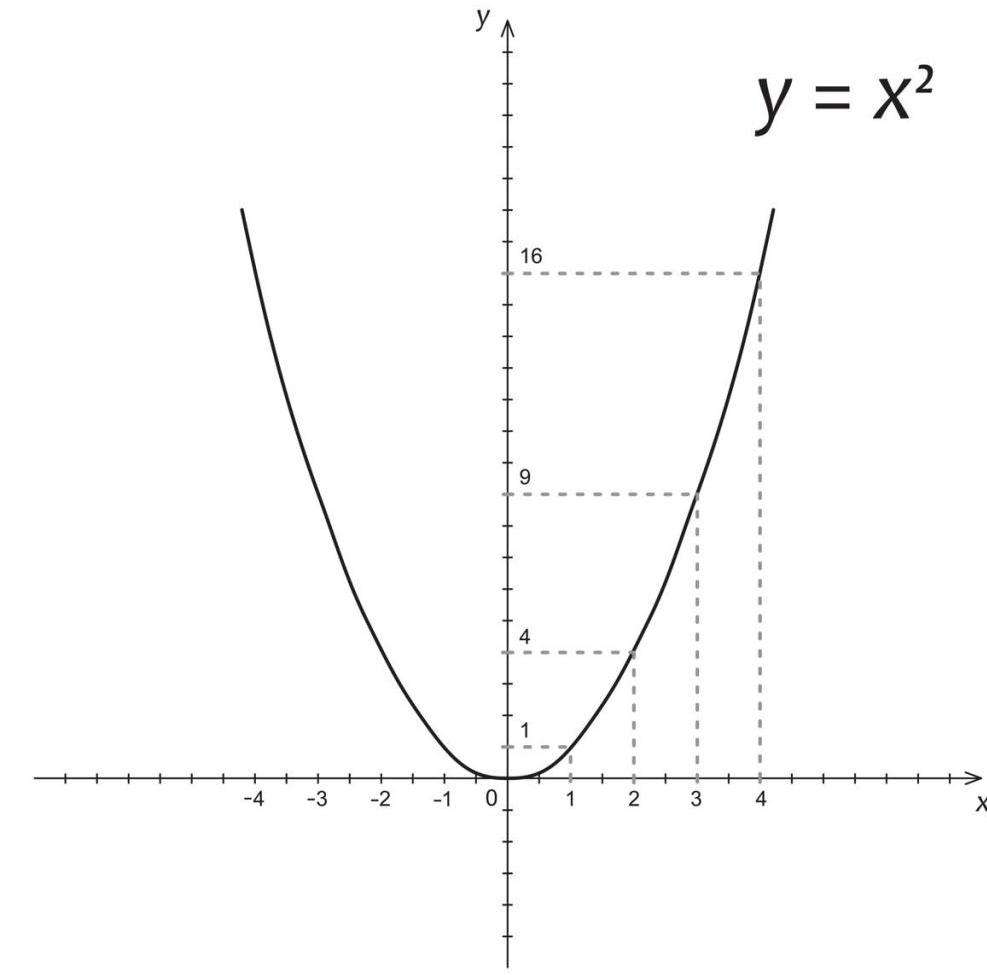
Парабола
1. Определяем, куда направлены ветви параболы.
2. Приравниваем функцию к нулю и находим корни уравнения.
3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.
Выписываем в виде функции:
Приравниваем к нулю.
Дальше решаем как квадратное уравнение и находим нули функции:
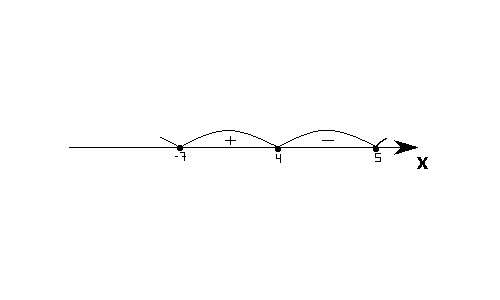
Метод интервалов
1. Находим корни уравнения, при которых неравенство равно нулю.
2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.
3. Определяем знак любого интервала.
4. Расставляем знаки у остальных интервалов, меняя их через один.
2) Изображаем их на числовой прямой.
3) Определяем знаки интервалов.
2. Отмечаем их на числовой прямой.
3. Определяем знаки интервалов.
Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.
Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.
Системы уравнений
Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.
Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.
Алгебраический метод
Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.
Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:
Решаем получившееся уравнение и находим икс.
Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:
Метод подстановки
Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.
В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:
Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:
Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:
Конспект урока по математике на тему » Может ли величина изменяться?» (4 класс)
Может ли величина изменяться?
I. Устный счет.
1. Разгадайте правило, по которому
составлена схема, и вставьте числа в «окошки».
в 3 раза меньше, чем сорока, а ворона на 40 лет больше,
чем ласточка. Сколько лет может прожить ворона?
– Составьте все обратные задачи к данной.
– Сколько треугольников на чертеже?
II. Сообщение темы урока.
Прочитайте записи на доске:
а) длина, высота, красота, ширина;
б) возраст, рост, вес.
– В первой строчке найдите «лишнее» слово. (Красота.)
– Что объединяет слова второй строчки? (Это величины.)
– Сегодня ответим на вопрос: «Может ли величина изменяться?»
III. Работа по учебнику.
Задание 91. Учащиеся выполняют измерения и заполняют таблицу.
Какая величина не изменяется при переходе от одного из данных прямоугольников к другому? (Ширина.)
– Такую величину называют постоянной.
– Какая величина изменяется при переходе от одного из данных прямоугольников к другому? (Длина.)
– Такая величина называется переменной.
– Что можно сказать о площади этих прямоугольников? (Эта величина будет переменной при переходе от одного из данных прямоугольников к другому.)
– Площадь будет постоянной или переменной при изменении только одной из сторон прямоугольника? (Будет переменной.)
– Будет ли площадь одной и той же данной фигуры всегда величиной постоянной, или она может изменяться в зависимости от положения фигур? (Будет постоянной.)
Задание 92. Среди перечисленных величин укажите те, которые являются переменными. (Рост человека в течение жизни; масса человека в течение жизни; масса стакана с водой по мере наполнения его этой водой; число учащихся класса за все годы обучения.)
Задание 93. Рассмотрите таблицу. В течение какой недели число учащихся, присутствующих на занятиях, было постоянным? (В течение первой недели.) А в течение какой было переменным? (В течение второй недели.)
Задание 94. Приведите по три примера постоянных величин из окружающей действительности. (Площадь доски; высота стакана.)
– Приведите по три примера переменных величин из окружающей действительности. (Толщина тетради; масса корзины с яблоками; длина волос.)
Задание 95. Учащиеся заполняют таблицу.
Решение: 1) Р 1 = (24 + 1) · 2 = 25 · 2 = 50 (см)
S 1 = 24 · 1 = 24 (кв. см)
2) Р 2 = (12 + 2) · 2 = 24 · 2 = 48 (см)
3) Р 3 = (8 + 3) · 2 = 11 · 2 = 22 ( см )
4) Р 4 = (6 + 4) · 2 = 10 · 2 = 20 (см)
S 4 = 6 · 4 = 24 (кв. см)
– Какая из перечисленных в таблице величин не изменяется при переходе от одного прямоугольника к другому? (Площадь.)
– А какие изменяются? (Длина, ширина, периметр.)
Задание 96. Начертите три ломаных линии, длина которых при переходе от одной к другой остается постоянной, а число звеньев уменьшается.
а) 20 см = 1 см + 2 см + 8 см + 5 см + 4 см;
б) 20 см = 3 см + 8 см + 5 см + 4 см;
в) 20 см = 3 см + 8 см + 9 см.
Задание 97. Начертите три окружности,
радиусы которых при переходе по порядку
от одной к другой увеличиваются.
Задание 98. Начертите три ломаные линии,
длина которых при переходе по порядку от одной
к другой уменьшается, а число звеньев остается
а) 10 см = 5 см + 3 см + 2 см;
б) 9 см = 4 см + 3 см + 2 см;
в) 8 см = 3 см + 3 см + 2 см.
– Может ли одновременно число звеньев ломаной линии увеличиваться, а длина уменьшаться? (Может.)
Постоянная и переменная величина.
Развитие математики в изучении законов природы и использования этих законов в технике привело к вводу понятий переменной и постоянной величин.
Переменные и постоянные величины. Эти величины в вопросе, который изучается, имеют разные значения или, что относится к постоянной величине, остаются с одним значением постоянно. К примеру, когда изучается падение тела, расстояние до земли, а так же скорость падения — величина переменная, в то время как ускорение (только есть не брать в учет воздушное сопротивление) — постоянная величина.
Поговорим о переменной величине. В условиях нашего вопроса может принять разные значения.
И о постоянной величине. При условии нашего вопроса остается без изменений. Однако одна величина в разных ситуациях может оказаться переменной либо постоянной.
Например, температура T кипения воды в основном это постоянная величина со значением T = 100 °С. Но в ситуациях, когда необходимо учитывать изменения атмосферного давления, температура кипения воды становится переменной величиной.
Областью изменения переменной величины называется совокупность всех принимаемых ею числовых значений. Область изменения может состоять как из одного или нескольких промежутков, так и из одной точки.
Разделение величин переменных и постоянных зачастую применяют в высшей математике, в то время как в элементарной математике в основном разделение величин происходит на известные и неизвестные. Разделение на известные и неизвестные величины есть и в высшей математике, однако занимает не главное место.
Что такое переменная величина в математике
Содержание статьи
Переменные
Основным показателем переменной является то, что она записывается не числом, а буквой. Под условным обозначением чаще всего скрывается определенное значение. Переменная получила свое название благодаря тому, что ее значение меняется в зависимости от уравнения. Как правило, любая буква алфавита может быть использована в качестве обозначения для такого элемента. Например, если вы знаете, что у вас есть 5 рублей и вы хотите купить яблоки, которые стоят 35 копеек, конечное количество яблок, которые можно купить, обозначается буквой (например «С»).
Пример использования
Если есть переменная, которая была выбрана по вашему усмотрению, необходимо составить алгебраическое уравнение. Оно будет связывать между собой известные и неизвестные величины, а также показывать связь между ними. Это выражение будет включать в себя цифры, переменные и одну алгебраическую операцию. Важно отметить, что выражение будет содержать знак равенства.
Полное уравнение содержит значение выражения в целом. Оно отделено от остального уравнения знаком равенства. В предыдущем примере с яблоками 0.35 или 35 копеек, умноженные на «С», является выражением. Для того чтобы создать полное уравнение, необходимо записать следующее:
Мономиальные выражения
Полиномы
Зависимые и независимые переменные
В математике независимыми переменными являются неизвестные, которые определяют другие части уравнения. Они стоят отдельно в выражениях и не изменяются вместе с другими переменными.
Значения зависимых переменных определяются с помощью независимых. Их значения зачастую определяются эмпирически.