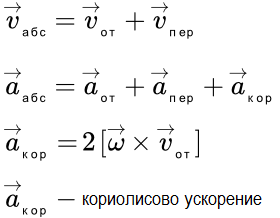Что такое переносное движение

Сложное движение точки. Теорема Кориолиса

Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где – кориолисово ускорение.

Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.

Сложное (составное) движение точки

Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.

Такое движение точки называется сложным или составным.

Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.

Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).

Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.

Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.

Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.

Относительная скорость и ускорение

Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.

Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.

Переносная скорость и ускорение

Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела.

Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.

Подставляем в (4):

.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.

Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где – угловое ускорение тела.

Абсолютная скорость и ускорение

Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат.

Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.

Теорема о сложении скоростей

При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.

Доказательство

Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1) ;
(7)
.

Теорема Кориолиса о сложении ускорений

При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
– кориолисово ускорение.

Доказательство

В последнем члене применим (6) и (2).

.
Тогда
.

Источник

Теоретическая механика

19. Сложное движение точки. Относительное, переносное и абсолютное движение точки.

Относительное, переносное и абсолютное движение точки

Выберем две системы отсчета – неподвижную и подвижную системы отсчета. Например, баржа, движущаяся относительно неподвижного берега (неподвижная система координат, связанная с неподвижным берегом) и человек идущий по движущейся барже (подвижная система координат, связанная с движущейся баржей).

Движение точки относительно подвижной системы отсчета называется относительным движением точки.

Движение точки вместе с подвижной системой отсчета относительно неподвижной системы отсчета называется переносным движением точки.

Движение точки относительно неподвижной системы отсчета называется абсолютным или сложным движением точки.

Очевидно, что скорость и ускорение движущейся точки связаны с выбором системы отсчета, относительно которой исследуется движение. Поэтому логично предположить, что производная по времени от радиус-вектора движущейся точки также будет связана с выбором системы отсчета. Для количественного отражения этой связи необходимо определить производную по времени в различных системах отсчета.

Абсолютная и относительная производные от вектора

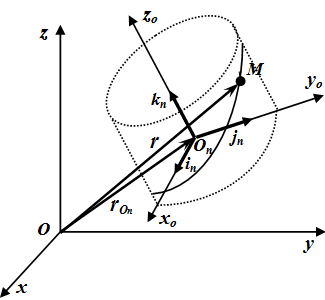
Пусть наблюдатель связан с подвижной системой координат (рис.К.16).

Тогда радиус-вектор движущейся точки в подвижной системе координат может быть представлен в виде

Для наблюдателя, связанного с подвижной системой координат, орты не меняют свое направление, поэтому можно записать

Таким образом, можно записать, что

Выражение (К.15) является записью абсолютной производной вектора по времени равной сумме относительной производной и векторного произведения

Источник

Переносное движение

Смотреть что такое «Переносное движение» в других словарях:

ПЕРЕНОСНОЕ ДВИЖЕНИЕ — в механике, движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной). (см. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор… … Физическая энциклопедия

ПЕРЕНОСНОЕ ДВИЖЕНИЕ — перемещение подвижной системы отсчёта (напр. движение вагона с передвигающимся в нём человеком), по отношению к которой точка, тело (человек) совершает относительное (см.) … Большая политехническая энциклопедия

ПЕРЕНОСНОЕ ДВИЖЕНИЕ — перемещение подвижной системы отсчета, по отношению к которой точка или тело совершает относительное движение … Большой Энциклопедический словарь

переносное движение — Движение подвижной системы отсчета по отношению к основной системе отсчета. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика … Справочник технического переводчика

переносное движение — 3.29 переносное движение : Совместное движение сооружения и основания во время землетрясения как единого недеформируемого целого с ускорениями (скоростями или смещениями) основания. Источник: СП 14.13330.2014: Строительство в сейсмических районах … Словарь-справочник терминов нормативно-технической документации

Переносное движение — В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения когда материальная точка движется относительно какой либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом … Википедия

переносное движение — движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной). * * * ПЕРЕНОСНОЕ ДВИЖЕНИЕ ПЕРЕНОСНОЕ ДВИЖЕНИЕ, перемещение подвижной системы отсчета, по отношению к которой точка или тело… … Энциклопедический словарь

переносное движение — nešamasis judėjimas statusas T sritis fizika atitikmenys: angl. bulk motion vok. Führungsbewegung, f rus. переносное движение, n pranc. mouvement d’entraînement, m; mouvement translatif, m … Fizikos terminų žodynas

ПЕРЕНОСНОЕ ДВИЖЕНИЕ — движение подвижной системы отсчёта по отношению к т. н. абсолютной (обычно инерциальной) системе отсчёта (см. Относительное движение) … Большой энциклопедический политехнический словарь

ПЕРЕНОСНОЕ ДВИЖЕНИЕ — движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной) … Естествознание. Энциклопедический словарь

переносное движение — Движение подвижной системы отсчёта по отношению к основной системе отсчёта … Политехнический терминологический толковый словарь

Источник

ПЕРЕНОСНОЕ ДВИЖЕНИЕ

ПЕРЕНОСНОЕ ДВИЖЕНИЕ в механике, движение подвижной системы отсчёта по отношению к системе отсчёта, принятой за основную (условно считаемую неподвижной); см. Относительное движение.

Переносное движение (Mouvement d‘entraînement). — Абсолютное движение точки и относительное движение ее по отношению к какому-либо движущемуся телу (см. Движение) суть два различных движения, находящиеся в некотором соотношении между собой и с движением посредствующего тела. В учении о движении доказывается, что абсолютное движение точки можно рассматривать как составное из относительного движения ее по отношению к посредствующему телу и из так называемого П. движения вместе с этим телом. Там же доказывается, что скорость абсолютного движения точки есть геометрическая сумма (см.) из скорости относительного движения и скорости той точки посредствующего тела, с которой движущаяся точка в рассматриваемый момент совпадает; последняя скорость называется скоростью П. движения. Говоря иначе: скорость абсолютного движения есть диагональ параллелограмма, построенного на скоростях движений относительного и П. Д. Б.

3.29 переносное движение : Совместное движение сооружения и основания во время землетрясения как единого недеформируемого целого с ускорениями (скоростями или смещениями) основания.

3.15 переносное движение: Cовместное движение сооружения и основания во время землетрясения как единого недеформируемого целого с ускорениями (скоростями или смещениями) основания.

Источник

Абсолютное, относительное и переносное движения точки

Абсолютное, относительное и переносное движения точки

Во введении в кинематику мы уже говорили, что всякое движение тела или точки есть движение относительное, т. е. его можно наблюдать и изучать лишь по отношению к другим телам и связанным с ними системам отсчета.

В предыдущих главах мы рассматривали движение по отношению к так называемой «неподвижной» системе отсчета, за которую в инженерной практике принимают обычно систему отсчета, жестко связанную с Землей.

Движение точки по отношению к системе отсчета, принимаемой за неподвижную, называется абсолютным движением.

В ряде случаев абсолютное движение точки бывает удобно рассматривать как сложное движение, состоящее из двух одновременных движений: движения точки по отношению к некоторой подвижной системе отсчета и движения точки вместе с подвижной системой отсчета по отношению к системе, принимаемой за неподвижную.

Так, например, движение какой-либо точки 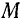колеса тепловоза (рис. 123) относительно Земли происходит по кривой, называемой циклоидой. Его можно считать состоящим из двух движений: движения точки по окружности по отношению к корпусу тепловоза и движения этой точки вместе с поступательно движущимся корпусом тепловоза.

Движение точки по отношению к подвижной системе отсчета называется относительным движением.

Движение подвижной системы отсчета и всех неизменно связанных с ней точек по отношению к системе отсчета, принимаемой за неподвижную, называется переносным движением.

Чтобы определить переносные скорость и ускорение какой-либо точки 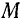в произвольный момент времени, надо мысленно прекратить относительное движение данной точки и определить в этот момент ее скорость и ускорение по отношению к неподвижной системе отсчета как точки, неизменно связанной с подвижной системой.

Аналогичным приемом бывает иногда удобно пользоваться и для выяснения относительного движения точки. Чтобы его определить, надо мысленно прекратить переносное движение точки.

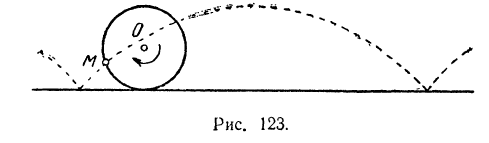
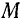
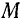
В приведенном выше примере круговое движение точки по отношению к движущемуся корпусу тепловоза есть, очевидно, относительное движение. Если эту точку мысленно неизменно связать с корпусом тепловоза, то ее движение вместе с ним будет переносным движением. Движение же точки (по циклоиде) по отношению к Земле — абсолютное движение.

Приведем для пояснения еще несколько примеров. Движение человека по палубе движущегося по реке парохода есть движение относительное. Движение точки палубы парохода, в которой в данный момент находится человек, относительно берега реки — переносное движение, а движение человека относительно берега — абсолютного движение.

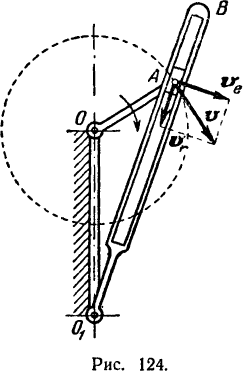
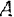
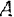
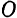
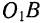
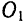
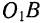
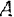
В механизме строгального станка (рис. 124) абсолютным движением точки (центра шарнира, соединяющего ползун с кривошипом ) будет ее движение по отношению к неподвижной станине станка. Этим движением является, очевидно, круговое движение точки вокруг неподвижного центра . Данное движение можно разложить на составляющие: движение точки вдоль кулисы (подвижной направляющей) — относительное движение и вращательное (колебательное) движение вокруг центра той точки кулисы , с которой совпадает в данный момент точка — переносное движение.

Еще раз подчеркнем, что термины «неподвижная» и «подвижная» системы отсчета имеют условное значение. Так, например, при рассмотрении движения точки колеса тележки, катящейся по палубе парохода, можно принять за «неподвижную» какую-либо систему отсчета, неизменно связанную с палубой (находящейся в движении по отношению к Земле).

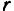
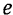
Условимся в дальнейшем обозначать все кинематические характеристики, относящиеся к абсолютному движению точки, принятыми ранее символами, а характеристики, относящиеся к относительному и переносному движениям точки, теми же символами, но с подстрочными индексами: — для относительного движения (от латинского слова relativus—относительный) и — для переносного движения (от французского слова entra-iner — увлекать с собой).

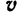
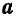
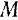
Абсолютной скоростью и абсолютным ускорением какой-либо точки называется ее скорость и ускорение по отношению к системе отсчета, принятой за неподвижную.

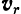
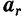
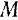
Относительной скоростью и относительным ускорением какой-либо точки называется ее скорость и ускорение по отношению к подвижной системе отсчета.

Несколько сложнее и требуют разъяснения понятия переносной скорости и переносного ускорения точки в тех случаях, когда движение подвижной системы отсчета не является поступательным.

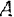
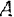
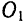
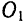
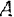
Так, в приведенном выше примере переносным движением точки (центра шарнира ползуна) является абсолютное движение, т. е. движение по отношению к неподвижной системе отсчета (к станине станка) той точки кулисы, с которой совпадает в данный момент точка . Но при вращении кулисы около неподвижной точки различные точки кулисы, находящиеся на различных расстояниях от точки и имеют различные скорости и ускорения, и потому переносные скорость и ускорение точки будут зависеть от того, какое положение эта точка занимает в данный момент по отношению к кулисе.

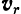
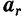
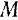
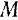
Таким образом, переносной скоростью и переносным ускорением какой-либо точки называется абсолютная скорость и абсолютное ускорение той, неизменно связанной с подвижной системой отсчета точки, с которой совпадает в этот момент данная точка .

Так как только при поступательном движении подвижной системы отсчета скорости и ускорения всех связанных с ней точек одинаковы, то только в этом случае переносная скорость и переносное ускорение движущейся точки не будут зависеть от ее положения относительно подвижной системы отсчета и под ними в этом случае можно понимать скорость и ускорение любой точки подвижной системы отсчета относительно неподвижной.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник