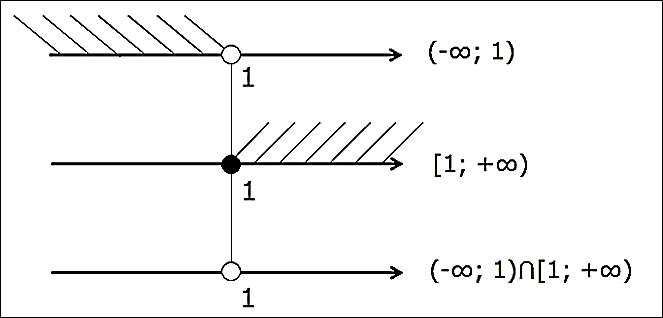
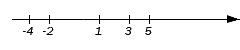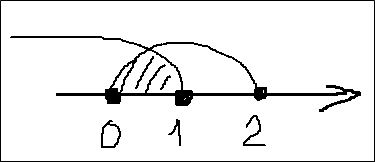Что такое пересечение и объединение промежутков

Числовые промежутки. Пересечение и объединение числовых промежутков

Отметим на координатной прямой точки с координатами –3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше –3 и меньше 2. Верно и обратное: если число х удовлетворяет условию –3

Множество всех чисел, удовлетворяющих условию –3 числовым промежутком или просто промежутком от –3 до 2 и обозначается так: (–3; 2).

На рисунках изображено множество чисел х, для которых выполняется неравенство х \(-\infty\) ; 10) и ( \(-\infty\) ; 10]. Читается так: число х принадлежит промежутку от минус бесконечности ( \(-\infty\) ) до 10 (х \(-\infty\) ) до 10, включая число 10 (х ≤ 10). Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

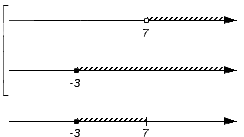
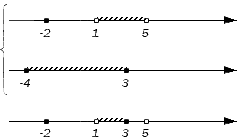
Промежуток [3; 5] является пересечением промежутков [–1; 5] и [3; 7]. Это можно записать так: [–1; 5] ∩ [3; 7] = [3; 5].

Промежутки [0; 4] и [6; 10] не имеют общих элементов. Если множества не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0; 4] ∩ [6; 10] = 0.

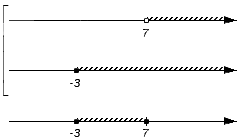
Каждое число из промежутка [1; 7] принадлежит хотя бы одному из промежутков [1; 5] и [3; 7], то есть, либо промежутку [1; 5], либо промежутку [3; 7], либо им обоим.

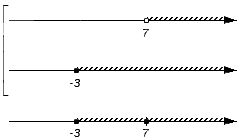
Промежуток [1; 7] является объединением промежутков [1; 5] и [3; 7]. Это можно записать так: \([1;5]\cup[3;7]=[1;7].\)

Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество \([0;4]\cup[6;10]\) не является промежутком.

Запишите двойное неравенство \(-2 в виде промежутка.

Найдите количество целых решений неравенства.

Источник

Нахождение пересечения и объединения числовых множеств, что такое пересечение множеств

Решение некоторых математических задач предполагает нахождение пересечения и объединения числовых множеств. В статье ниже рассмотрим эти действия подробно, в том числе, на конкретных примерах. Полученный навык будет применим для решения неравенств с одной переменной и систем неравенств.

Простейшие случаи

Когда мы говорим о простейших случаях в рассматриваемой теме, то имеем в виду нахождение пересечения и объединения числовых множеств, представляющих из себя набор отдельных чисел. В подобных случаях будет достаточно использования определения пересечения и объединения множеств.

Объединение двух множеств – это множество, в котором каждый элемент является элементом одного из исходных множеств.

Пересечение множеств – это множество, которое состоит из всех общих элементов исходных множеств.

Из указанных определений логически следуют следующие правила:

— чтобы составить объединение двух числовых множеств, имеющих конечное количество элементов, необходимо записать все элементы одного множества и дописать к ним недостающие элементы из второго множества;

— чтобы составить пересечение двух числовых множеств, необходимо элементы первого множества один за другим проверить на принадлежность второму множеству. Те из них, которые окажутся принадлежащими обоим множествам и будут составлять пересечение.

Полученное согласно первому правилу множество будет включать в себя все элементы, принадлежащие хотя бы одному из исходных множеств, т.е. станет объединением этих множеств по определению.

Множество, полученное согласно второму правилу, будет включать в себя все общие элементы исходных множеств, т.е. станет пересечением исходных множеств.

Рассмотрим применение полученных правил на практических примерах.

Решение

Однако на практике, чтобы найти объединение и пересечение трех и более простейших числовых множеств, которые состоят из конечного количества отдельных чисел, удобнее применять правила, аналогичные указанным выше.

Что же касается решения задачи на нахождение пересечения трех и более числовых множеств, которые состоят из конечного количества отдельных чисел, необходимо одно за другим перебрать числа первого множества и поэтапно проверять, принадлежит ли рассматриваемое число каждому из оставшихся множеств. Для пояснения рассмотрим числовые множества:

Координатная прямая и числовые промежутки как объединение их частей

Как определить пересечение и объединение при помощи изображений числовых множеств

С темой нахождения пересечения и объединения множеств возможно наглядно разобраться, если использовать изображения заданных множеств на координатной прямой (если только речь – не о простейших случаях, рассмотренных в самом начале статьи).

Мы рассмотрим общий подход, который позволяет определить результат пересечения и объединения двух числовых множеств. Опишем подход в виде алгоритма. Рассматривать его шаги будем постепенно, каждый раз приводя очередной этап решения конкретного примера.

Решение

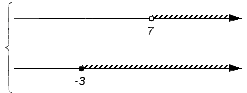
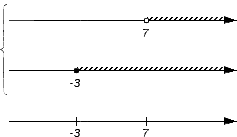
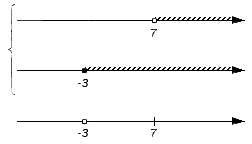
В нашем примере для записи пересечения и объединения числовых множеств имеем: и

и

Теперь необходимо поочередно проверить принадлежность каждого из записанных множеств искомому пересечению или объединению. Получаемые выводы поэтапно отмечаются на нижней координатной прямой: когда промежуток является частью пересечения или объединения, над ним рисуется штриховка. Когда точка входит в пересечение или объединение, то штрих заменяется на сплошную точку; если точка не является частью пересечения или объединения – ее делают выколотой. В этих действиях нужно придерживаться таких правил:

-. промежуток становится частью пересечения, если он одновременно является частью множества A и множества B (или иными словами – если есть штриховка над этим промежутком на обеих координатных прямых, отображающих множества А и B );

— точка становится частью пересечения, если она является одновременно частью каждого из множеств А и В (иными словами – если точка является невыколотой или внутренней точкой какого-либо интервала обоих числовых множеств A и B );

— точка становится частью объединения, если она является частью хотя бы одного из множеств A и B (иными словами – точка является невыколотой или внутренней точкой какого-либо интервала хотя бы одного из множеств A и B ).

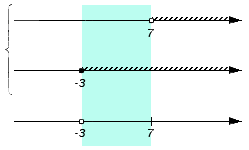
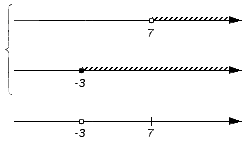
Оно является частью множества B (над интервалом присутствует штриховка), но не входит в множество A (над интервалом штриховка отсутствует): не будет входить в искомое пересечение, а значит на нижней координатной прямой не появляется никаких новых отметок:

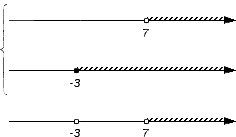
Промежуток входит в оба множества A и B (над промежутком присутствует штриховка), следовательно, становится частью пересечения. Штрихуем место над рассмотренным промежутком:

Имея некий практический опыт применения правил нахождения пересечений и объединений множеств, описанные проверки легко проводятся устно, что позволяет быстро записывать конечный результат. Продемонстрируем на практическом примере, как выглядит его решение без детальных пояснений.

Решение

Отметим заданные числовые множества на координатных прямых, чтобы иметь возможность получить иллюстрацию искомых пересечения и объединения:

Также понятно, что при достаточном понимании процесса указанный алгоритм возможно подвергнуть оптимизации. К примеру, в процессе нахождения пересечения можно не тратить время на проверку всех промежутков и множеств, представляющих собой отдельные числа, ограничившись рассмотрением только тех промежутков и чисел, которые составляют множество А или В. Прочие промежутки в любом случае не войдут в пересечение, т.к. не являются частью исходных множеств. Составим иллюстрацию сказанного на практическом примере.

Необходимо определить пересечение исходных множеств.

Решение

Геометрически изобразим числовые множества А и В :

Граничные точки исходных множеств разобьют числовую прямую на несколько множеств:

В заключении статьи обговорим еще, как решить задачу о нахождении пересечения и объединения нескольких множеств (более 2 ). Сведем ее, как рекомендовалось ранее, к необходимости определения пересечения и объединения первых двух множеств, затем полученного результата с третьим множеством и так далее. А можно использовать описанный выше алгоритм с единственным только отличием, что проверку вхождения промежутков и множеств, представляющих собой отдельные числа, необходимо проводить не по двум, а всем заданным множествам. Рассмотрим на примере.

Решение

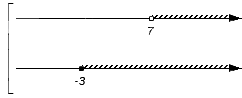
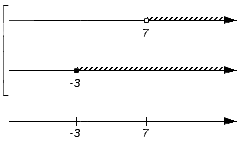
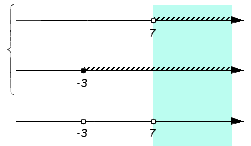
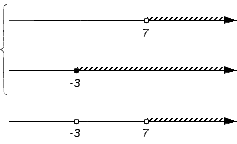
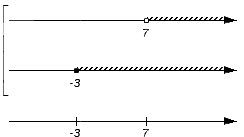
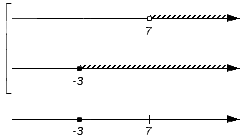
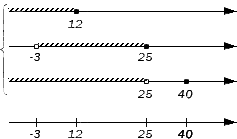
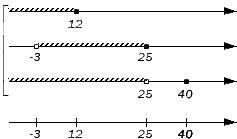
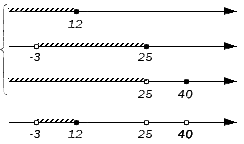
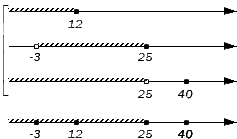
Отображаем заданные числовые множества на координатных прямых и ставим с левой от них стороны фигурную скобку, обозначая пересечение, а также квадратную, обозначая объединение. Ниже отобразим координатные прямые с отмеченными штрихами граничными точками числовых множеств:

Отметим также, что искомое пересечение числовых множеств часто является пустым множеством. Происходит это в тех случаях, когда в заданные множества не включены элементы, одновременно принадлежащие им всем.

Решение

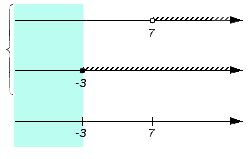
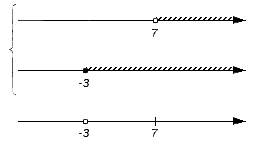
Отобразим исходные множества на координатных прямых и штрихами граничные точки этих множеств на дополнительной прямой.

Ни одно из них не является одновременно элементом всех исходных множеств, следовательно, пересечение заданных множеств есть пустое множество.

Множества удобно изображать в виде кругов, которые называют кругами Эйлера.

На рисунке множество пересечения множеств X и Y закрашено в оранжевый цвет.

Источник

Интервалы и область определения-2

Если необходимо искать несколько промежутков, то лучше использовать «навесы», чтобы визуально легче найти решение.

Например, здесь у нас есть два промежутка: (1; 4] и (2; 5)

Если нам надо найти пересечение промежутков, т.е. область, которая соответствует и первому и второму промежутку, то мы записываем так (выгнутой буквой П)

(1; 4] (2; 5) ∈ (2; 4]

Видно, что 2 не включена во вторую область, поэтому мы ставим её в круглых скобках, а 4 включено и в первую и вторую, поэтому мы ставим её в квадратных.

Говоря словами: «пересечение промежутков один-четыре и два-пять является область от 2 до 4, не включая 2».

Если мы хотим найти объединение промежутков, то мы используем обрезанное сверху знак похожий на латинскую «U» и на графике берем все точки под всеми навесами:

(1; 4] (2; 5) ∈ (1; 5)

Если возникает такая ситуация:

То пересечений («П») здесь нет:

(-∞; 0) [1; 4) ∈ Ø и мы это обозначаем, как пустое множество Ø.

А если от нас захотят узнать объединение этих промежутков, мы просто запишем в ответе так: (-∞; 0] ​​​​​​​ [1; 4)

Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание

Добавить интересную новость

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

При правильном ответе Вы получите 2 балла

Какие точки входят в данный интервал: (-4; 2] (1; 5)

Выберите те ответы, которые считаете верными.

Добавление комментариев доступно только зарегистрированным пользователям

Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.

Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Источник

Как пересекать промежутки?

Операции над числовыми промежутками.

Операций над промежутками совсем немного. Всего две. Это пересечение и объединение. При решении серьёзных заданий с неравенствами эти две операции над промежутками необходимо проделывать постоянно. В самых разных сочетаниях. По своей сути это очень простые операции. Но, справедливости ради, эти самые операции являются вторым источником досадных ошибок при решении неравенств после тождественных преобразований. Разберёмся?

Пересекать и объединять числовые промежутки, проще всего при помощи числовой оси. Начнём с пересечения, оно хоть и проще в визуальном восприятии, но простора для ошибок даёт больше…

Как пересекать промежутки?

Сама по себе операция пересечения промежутков совсем простая. Тем не менее, именно пересечение промежутков — самая богатая на сюрпризы операция, которая столько людей ушибла! И очень больно ушибла. Но мы-то с вами — люди думающие и осторожные! С сюрпризами разберёмся, да и под ноги смотреть будем.) И не споткнёмся на ровном месте.

Итак, для начала запоминаем:

Пересечением двух числовых промежутков называется их общая часть.

И всё! Смутить могут только слова «общая часть». Всё просто. Общая часть — это те точки (или кусочки оси), которые одновременно входят в каждый из промежутков. Слова «общая часть» и «одновременно» здесь синонимы. Если раз и навсегда разобраться в этих нехитрых словах, то при ответе на любой вопрос о пересечении любых промежутков вы даже не заметите проблем! Намёк понятен?)

Возможно, вы до сих пор в сомнениях, но картинка с числовой осью, наш главный помощник, всё сразу же прояснит! Это только на конкретных примерах показать можно.

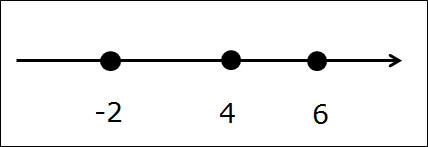
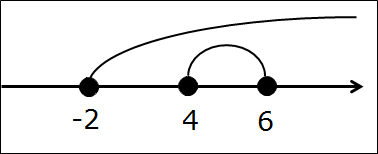
Начнём с совсем простенького, безо всяких подводных камней в виде выколотых точек. Допустим, нам надо пересечь два промежутка:

Первым делом рисуем числовую ось, отмечаем все граничные точки правильными кружочками. Они здесь — чёрные:

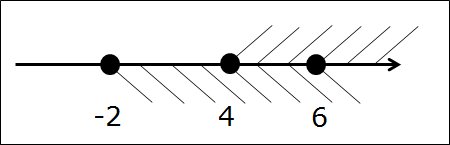
Вот так. Следующим шагом подштриховываем оба промежутка на одной оси. Чтобы не запутаться, для отличия пользуемся штриховкой с разных сторон оси в разных направлениях. Не нужно ювелирно штриховать по линеечке, мы не на черчении. Штрихуем грубо, брутально, но — разборчиво. Где-то штриховки будут встречаться одна под другой, образуя «ёлочку», но ничего не смущаемся, это — именно то, что нам и нужно! Получим такую картинку:

А теперь смотрим и соображаем: какой кусочек числовой оси подштрихован обоими видами штриховки одновременно? Верно! Кусочек между точками 4 и 6. Или — промежуток [4; 6]. Этот промежуток и будет пересечением промежутков [-2; 6] и [4; +∞). И все дела.)

Математически результат пересечения оформляют вот так:

[-2; 6] ⋂ [4; +∞) = [4; 6]

Значок «⋂» означает «пересечение».

Разбираем следующий пример. Пример совсем безобидный, но ступор у некоторых случается, да…)

Пересечём, например, промежутки:

Рисуем. В этот раз я буду использовать второй способ рисования — дужки. Получим такую картинку:

И опять соображаем: какой кусок оси содержит точки обоих промежутков одновременно?

Не догадались? Тогда снова штрихуем промежутки в разных направлениях, прямо под дужками. И смотрим, где штриховки накладываются:

Ну и как, осенило? Да! Второй промежуток [4; 6] — и есть наше пересечение (т.е. общая часть)! Да, весь целиком. Дело всё в том, что второй промежуток, [4; 6], целиком содержится в первом [-2; +∞). Ничего страшного, так бывает.

В математической форме:

[-2; +∞) ⋂ [4; 6] = [4; 6]

Уловили идею? Ну-ка, быстренько закрепим успех!

Найдите пересечения следующих числовых промежутков:

Ответы (в беспорядке):

Что, примитив? Ну да, проще некуда. А вот сейчас начинаются первые сюрпризы! Я же обещал…)

Сюрприз первый — пустое множество

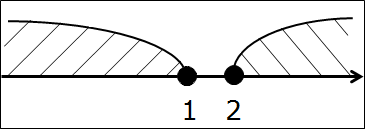
Попробуем пересечь, скажем, такие два промежутка:

(-∞; 1] ⋂ [2; +∞)

Дело нехитрое. Рисуем ось, точки-кружочки, помечаем дужками каждый промежуток, штрихуем, всё чин-чинарём…

И? Где здесь общая часть? А нигде! Нету такого кусочка оси, который был бы закрашен разными штриховками одновременно. На нет и суда нет. В таких случаях говорят, что данные промежутки не пересекаются.

Математически эта фишка записывается вот как:

(-∞; 1] ⋂ [2; +∞) = Ø

Этот перечёркнутый кружочек означает «пустое множество». Множество, в котором нет ни одного элемента. Ни одного числа… Очень частое явление. Особенно — при решении систем неравенств.

Сюрприз второй — изолированная точка

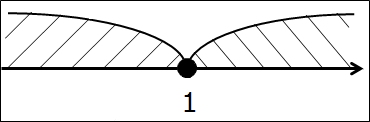
Всё то же самое, что и в предыдущем примере, только двойку во втором промежутке заменю на единичку. Вот так:

(-∞; 1] ⋂ [1; +∞)

Делать нечего, опять рисуем ось. В этот раз рисуем одну единственную точку 1. Закрашенную.

А здесь какие мысли насчёт пересечения? Да! Единственная общая часть — точка 1. Одна точка. Любая другая точка — правее ли единички, левее ли — попадает лишь в один из пересекаемых промежутков. Либо только в левый, либо только в правый. И только лишь единичка попадает в оба промежутка сразу.

В таких случаях результат пересечения (одна точка) оформляют так:

(-∞; 1] ⋂ [1; +∞) =

Фигурные скобочки в такой записи означают множество. Числовое множество. Единичка внутри фигурных скобок — элемент этого множества. Один-единственный. Или — изолированная точка.

Не следует думать, что пустое множество и изолированная точка –такая уж экзотика при решении неравенств. Такие сюрпризы попадаются в системах неравенств, в методе интервалов, в нахождении области определения функции, в уравнениях/неравенствах с модулем и прочих серьёзных темах. В соответствующих уроках убедимся.)

Кто читает вдумчиво, тот заметил, что слово «множество» я употребил в этом уроке уже не один раз. И это неспроста. Дело в том, что числовые промежутки и операции над ними — это знакомство с ещё одним новым разделом математики, помимо неравенств. Раздел называется «Теория множеств» и работает именно с множествами объектов самой разной природы. Числовыми промежутками, в том числе. Но множества — отдельная большая тема. Не в этот раз…

Полдела сделано. Можно заниматься наскальной живописью. Что-то типа такого:

Несведущий человек отшатнётся в ужасе. А сведущий сразу твёрдой рукой напишет:

(-∞; 1] ⋂ [0; 2] = [0; 1].

Так обычно оформляют пересечение промежутков в большинстве школ. Рисуют ось, штрихуют промежутки, ищут общую часть, да и записывают ответ. Такой способ хорош только в самых простых случаях. Пока точки — чёрные.

Проблемы начинаются с появлением выколотых точек.

Как работать с выколотыми точками?

Как только в игру вступают выколотые (т.е. незакрашенные) точки, вся простота куда-то испаряется напрочь… Особенно, если одна и та же точка в разные промежутки входит по-разному. Где-то она выколота, где-то закрашена… И в каком виде рисовать её на одной оси? Закрашивать её или нет?! Вот и путается народ…

Более того, обратите внимание! Во всех примерах этого урока мы пересекаем лишь два промежутка. Для простоты и понимания сути. А в более продвинутых заданиях (системы неравенств, нахождение ОДЗ и прочие крутые штучки) приходится пересекать и три, и пять… И все с разными кружочками и скобочками… Как не запутаться?

Есть, есть один секретный способ не запутаться! Но о нём — в конце урока.

А пока фиксируем в памяти одну простую вещь:

Операция пересечения — штука жёсткая. Если точка НЕ входит хотя бы в ОДИН из пересекаемых промежутков, то она автоматически НЕ входит и в окончательный результат пересечения.

Поясняю. Если какая-то точка хотя бы в одном из промежутков является выколотой, то нас уже не волнует, что там у неё с остальными промежутками (вторым, третьим, пятым…) — входит она в них или нет: в окончательный ответ такая точка УЖЕ не войдёт. Типа, даже если вы положили в борщ картошку, морковку, свёклу, лук, но в конце посолили стиральным порошком, кушать такой борщ вы уже не будете, да…) Уловили?

Разберём ценные зелёные слова на практике. Был у нас в самом начале урока примерчик:

[-2; 6] ⋂ [4; +∞)

А теперь я немного видоизменю в нём один из промежутков. Сделаю во втором промежутке точку 4 выколотой. Т.е. скобочка перед четвёркой станет круглой. Вот такое пересечение теперь рассмотрим:

[-2; 6] ⋂ (4; +∞)

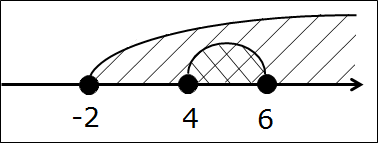
Рисуем, штрихуем, получаем картинку:

Ищем общую часть, записываем ответ:

[-2; 6] ⋂ (4; +∞) = (4; 6]

Кто в теме и врубился в слова «общая часть» и «одновременно», тот сразу всё понял. А кто не в теме, то… начинаем рассуждать. Примерно так:

А шестёрка? Тут без вопросов: в первый промежуток число 6 попадает на границу, но в закрашенном виде, а во второй (4; +∞) входит явно. Входит одновременно в оба? Да! Рисуем квадратную скобку: …6].

Итого: (4; 6].«

Вот так. Я же говорил, что ключевое слово здесь — одновременно!

Здесь-то ещё просто. А бывает куда злее! Когда неясно, как даже рисовать картинку-то… Например:

(-∞; 1) ⋂ [1; +∞)

Всё как обычно, рисуем прямую и отмечаем одну единственную граничную точку 1.

И… что-то не рисуется… В первом промежутке единичка с круглой скобкой, во втором — с квадратной. А ось — одна… Каким именно кружочком — пустым или закрашенным — рисовать единицу на оси? Непонятно…

Непонятно, если не понимать сути операции пересечения. А если понимать, то проблем — никаких. Наша граничная точка 1 в первый промежуток (-∞; 1) не входит. Выколота. Стало быть, при пересечении нам уже без разницы, закрашена ли единица во втором промежутке [1; +∞): в окончательный ответ она УЖЕ не войдёт!

Вывод: на оси точка 1 изображается выколотой. Т.е. незакрашенной.

Штриховки нигде не накладываются, а единственная разделяющая точка 1 — выколота. Ответ очевиден — пустое множество:

(-∞; 1) ⋂ [1; +∞) = Ø

Обычно именно так и поступают со всеми подозрительными точками. Берут конкретную точку, поочерёдно подставляют её в каждый из промежутков, анализируют, входит/не входит, и если хоть куда-то не входит — вычёркивают отовсюду. Так рисуются все белые точки. Потом собирают все точки, которые входят одновременно во все промежутки. И рисуют чёрными… И только потом рисуют окончательную картинку… Кошмар? Согласен, кошмар. Когда ось только одна, а точек разной раскраски — много.

Поэтому сейчас мы отдохнём от писанины и тягостных раздумий. А вместо этого — порисуем. Рисовать будем много, но зато результат окупится с лихвой. А количество ошибок резко сократится.)

Обещанный секретный способ!

Пересекаем промежутки без ошибок! Метод параллельных осей.

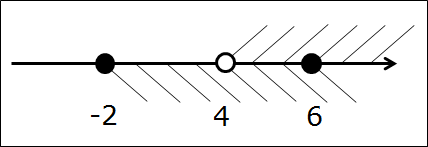
Итак, снова пересекаем те же самые промежутки: [-2; 6] ⋂ (4; +∞).

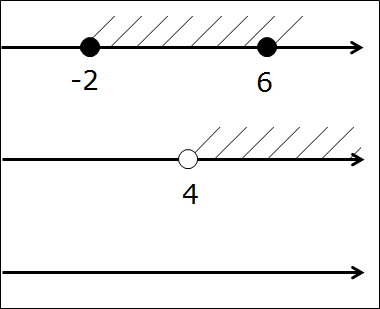
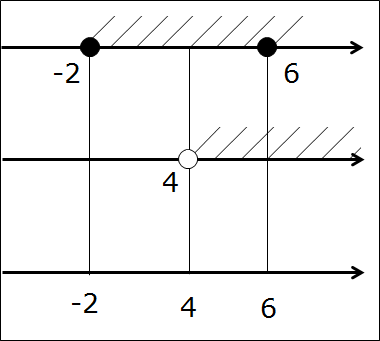
Сейчас берём в руки карандаш и рисуем… три параллельные оси! Всё правильно, именно три, я не обсчитался. На первых двух осях отдельно рисуем и штрихуем те промежутки, которые будем пересекать. Т.е. [-2; 6] и (4; +∞). На каждой из осей — свой. Соблюдаем одинаковый масштаб по всем трём осям! Это важно. Зачем нужна третья ось? Сейчас узнаем.) Получим такую картинку:

Представили? Вот так:

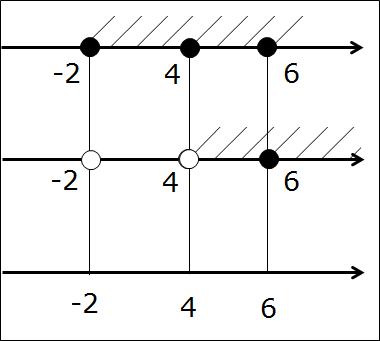
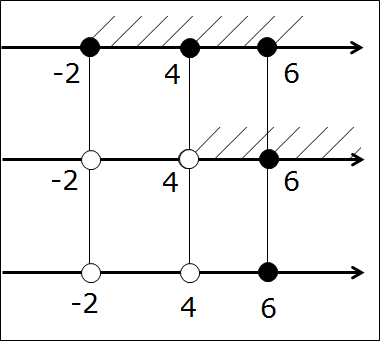
А нужны они нам — эти кружочки-то?! Ещё как! Самый ответственный, третий этап — рисуем нужные кружочки на третьей оси. Для этого рассуждаем так же, как и при прикидке в уме: если на первых двух осях обе точки чёрные, то и на третьей оси точка также чёрная. Если же хоть одна из двух точек выколота — на третьей оси точка также выколота!

Картинка станет вот такой:

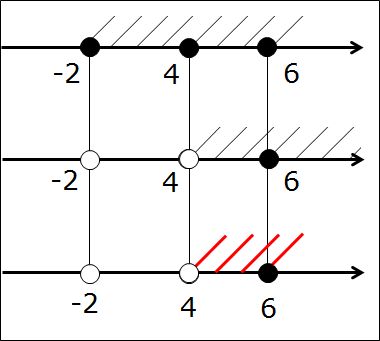
Остались пустяки. Четвёртым этапом штрихуем на третьей прямой тот её кусочек, который заштрихован на первых двух прямых одновременно. Вот так:

Ответ: (4; 6]

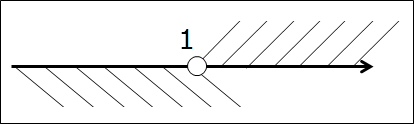
Решаем тот самый злой пример с единичкой и пустым множеством: (-∞; 1) ⋂ [1; +∞)

Рисуем картинку с тремя осями и сразу видим всю необходимую информацию:

Безо всяких сомнений ясно, что единичка — выколота, а штриховать на третьей оси и вовсе нечего…

Ответ: Ø

Переходим к следующей важной операции — к объединению промежутков. В следующем уроке…

Источник