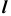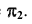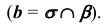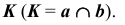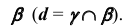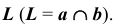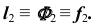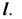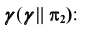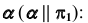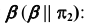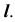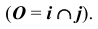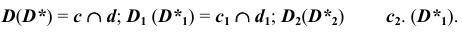Что такое пересечение плоскостей

Линия пересечения плоскостей онлайн

С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Линия пересечения плоскостей − теория, примеры и решения

Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α₁ и α₂:

Найдем уравнение линии пересеченя плоскостей α₁ и α₂. Для этого рассмотрим следующие случаи:

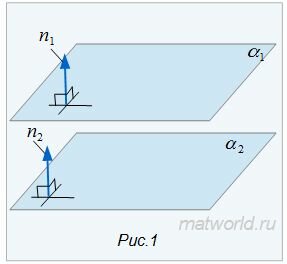Умножив уравнение (2) на λ, получим:

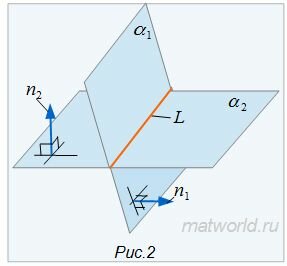Если векторы n₁ и n₂ не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:

Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.

Так как в системе линейных уравнений (4) векторы n₁=<A₁, B₁, C₁> и n₂=<A₂, B₂, C₂> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:

Равенство (5) можно записать в следующем виде:

Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α₁ и α₂. Полученное уравнение прямой можно записать в каноническом виде:

Пример 1. Найти линию пересечения плоскостей α₁ и α₂:

Поскольку направляющие векторы n₁ и n₂ неколлинеарны, то плолскости α₁ и α₂ пересекаются.

Для нахождения линии пересечения влоскостей α₁ и α₂ нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:

Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 2 со строкой 1, умноженной на −2:

Второй этап. Обратный ход Гаусса.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

где t− произвольное действительное число.

Запишем (11) в следующем виде:

Получили уравнение линии пересечения плоскостей α₁ и α₂ в параметрическом виде. Запишем ее в каноническом виде.

Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α₁ и α₂имеет вид:

Пример 2. Найти линию пересечения плоскостей α₁ и α₂:

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/2), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/2:

Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α₁ и α₂ не совпадают. Следовательно они параллельны, т.е. не пересекаются.

Пример 3. Найти линию пересечения плоскостей α₁ и α₂:

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/3), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/3:

Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α₁ и α₂ совпадают.

Источник

Построение линии пересечения плоскостей, заданных различными способами

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

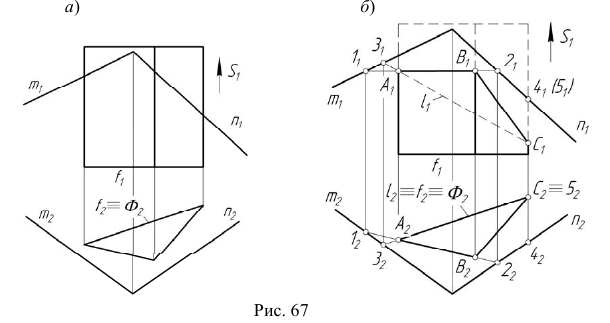
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L₁ и L₂, принадлежащих линии пересечения.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Пересечение плоскостей, заданных следами

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П₁ и П₂.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

Пересечение плоскостей треугольников

Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f_0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₂. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π₂. С противоположной стороны от линии N»K» видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₁. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π₁. С противоположной стороны от линии N’K’ видимость треугольников меняется.

Источник

Пересечение поверхностей в начертательной геометрии с примерами

Содержание:

Пересечение поверхностей:

В этом разделе рассмотрим решение задач по определению линии пересечения:

В зависимости от формы поверхностей, их взаимного положения и положения относительно плоскостей проекций используются различные способы построения их линии пересечения [3], [7].

В данном пособии рассмотрим следующие способы построения линии пересечения поверхностей:

Пересечение плоскостей

Способ вспомогательных секущих плоскостей Для построения линии пересечения плоскостей общего положения используется способ вспомогательных секущих плоскостей.

Рассмотрим общий алгоритм решения задачи по определению линии пересечения поверхностей (плоскостей) способом секущих плоскостей.

Задача:

Построить линию пересечения

Алгоритм решения

Для построения других точек искомой линии повторим указанный алгоритм необходимое количество раз.

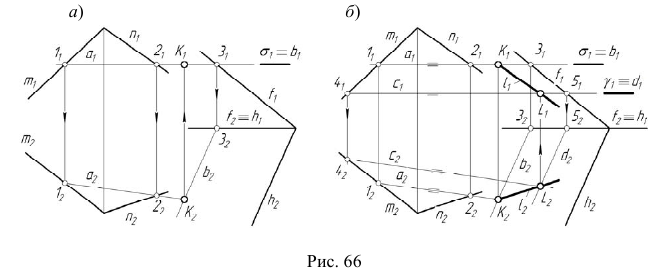
При решении задачи на пересечение плоскостей линии a и b представляют собой прямые линии, а рассмотренный алгоритм построения общих точек пересекающихся поверхностей применяется дважды.

Задача:

На эпюре Монжа построить линию пересечения плоскости с плоскостью (рис. 66).

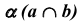
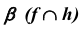
Решим эту задачу в соответствии с алгоритмом решения задачи 10. В качестве вспомогательных секущих плоскостей будем использовать, например, плоскости уровня 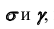параллельные

Алгоритм решения

1. Рассечем обе плоскости вспомогательной плоскостью 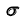(см. рис. 66, а).

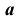
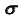
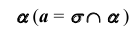
2. Определим линию пересечения плоскости с плоскостью в соответствии с алгоритмом решения задачи 6.

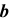
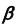
3. Определим линию пересечения плоскости с плоскостью

4. Определим проекции одной общей точки заданных плоскостей — точки

5. Рассечем обе плоскости вспомогательной плоскостью 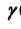(см. рис. 66, б).

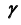
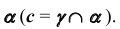
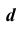
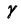
6. Определим линию пересечения c плоскости с плоскостью 7. Определим линию пересечения плоскости с плоскостью

8. Определим проекции еще одной общей точки заданных плоскостей — точки

9. Построим проекции искомой прямой линии, соединив соответствующие проекции точек K и L.

Пересечение плоскости общего положения с проецирующей поверхностью

Для определения линии пересечения плоскости общего положения с проецирующей поверхностью будем использовать собирательное свойство вырожденной проекции проецирующей поверхности и применять алгоритм построения линии, принадлежащей заданной плоскости.

Задача:

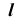
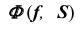
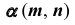
На эпюре Монжа построить проекции линии пересечения призматической проецирующей поверхности с плоскостью (рис. 67, а).

Алгоритм решения

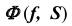
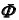
1. Так как призматическая поверхность — горизонтально- проецирующая, то вторая проекция линии пересечения поверхности с плоскостью совпадает с вырожденной горизонтальной проекцией поверхности (рис. 67, б).

Отметим горизонтальную проекцию

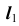
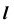
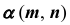
2. Фронтальную проекцию определим по принадлежности линии плоскости (рис. 67, б).

Пересечение плоскости общего положения с поверхностью общего положения

В этом разделе рассмотрим задачу, при решении которой используется способ секущих плоскостей.

Задача:

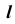
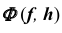
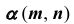
На эпюре Монжа построить проекции линии пересечения поверхности с плоскостью (см. рис. 68, а).

Для решения этой задачи в качестве вспомогательных плоскостей используем плоскости уровня, так как одна из проекций линии пересечения такой плоскости со сферой представляет собой прямую, а вторая — окружность.

Алгоритм решения

1. Определим проекции точек изменения видимости линии

а) Строим проекции точек A и B, используя в качестве вспомогательной плоскости — плоскость 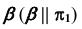(рис. 68, б):

б) Строим проекции точек С и D, используя в качестве вспомогательной плоскости плоскость уровня

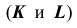
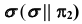
2. В соответствии с алгоритмом решения задачи 10 определим произвольные общие точки заданных фигур, используя в качестве вспомогательной плоскости плоскость уровня (рис. 68, в):

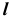
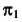
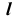
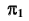
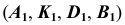
3. Определим видимость линии (рис. 68, г), используя точку K. При проецировании на плоскость точка K принадлежит невидимой части сферы, следовательно, часть линии от точки A до точки B, содержащая точку K, — невидимая. В поле проекций этот участок отметим штриховой линией.

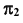
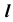
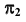
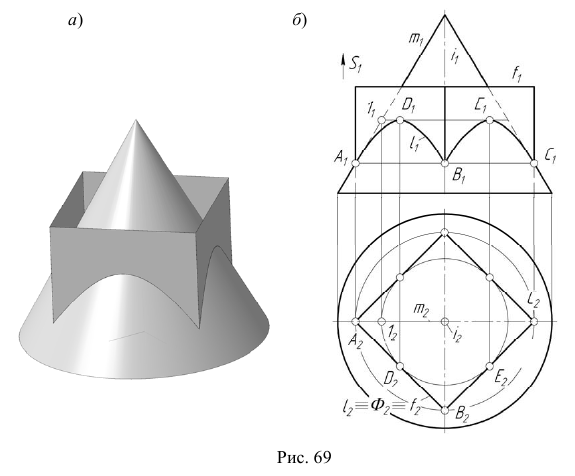
При проецировании на плоскость точка K принадлежит видимой части сферы, следовательно, часть линии от точки C до точки D, содержащая точку K, — видимая. В поле проекций этот участок отметим сплошной основной линией.

Пересечение проецирующей поверхности с поверхностью общего положения

Для определения линии пересечения проецирующей поверхности с поверхностью общего положения будем использовать собирательное свойство вырожденной проекции проецирующей поверхности и применять алгоритм построения линии, принадлежащей поверхности общего положения.

Задача:

На эпюре Монжа построить проекции линии пересечения 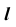проецирующей призматической поверхности с поверхностью общего положения (рис. 69, а).

Алгоритм решения

Проецирующие плоскости (грани призматической поверхности) пересекают коническую поверхность по гиперболическим кривым, фронтальными проекциями которых также будут гиперболические кривые.

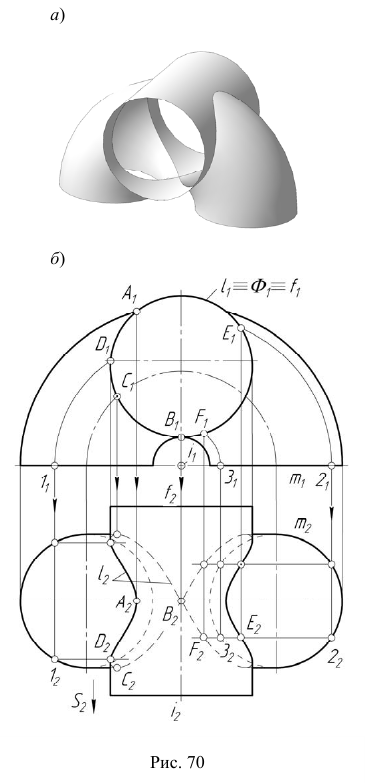
Задача:

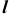
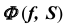
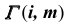
На эпюре Монжа построить проекции линии пересечения проецирующей цилиндрической поверхности с торовой поверхностью (рис. 70, а).

Вначале определим характер линии пересечения этих поверхностей и ее проекций.

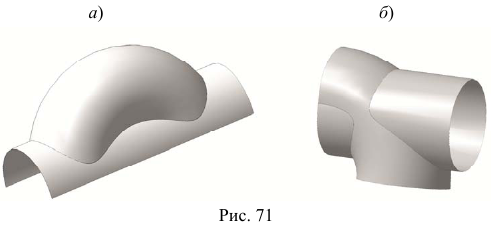
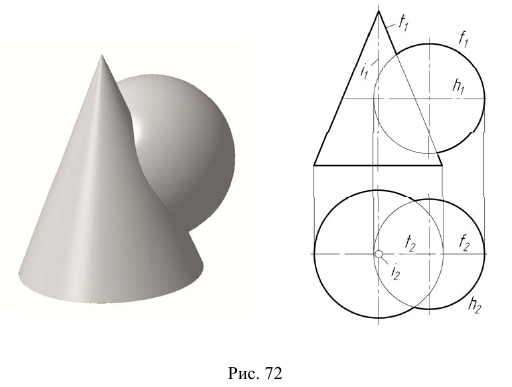
На основании теоремы о пересечении алгебраических поверхностей порядков n и m [3] цилиндрическая поверхность второго порядка пересекается с торовой поверхностью четвертого порядка в общем случае по пространственной кривой восьмого порядка (2·4=8) (рис. 71, а). При частном взаимном расположении поверхностей линия их пересечения может распадаться на две или более составляющих кривых меньших порядков (рис. 71, б).

В данной задаче линией пересечения являются две кривые четвертого порядка.

Алгоритм решения

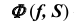
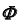
1. Так как поверхность — фронтально-проецирующая то первая проекция линии пересечения поверхностей совпадает с вырожденной фронтальной проекцией цилиндрической поверхности (рис. 70, б).

Отметим фронтальную проекцию

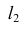
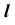
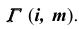
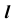
2. Горизонтальную проекцию определим по принадлежности линии поверхности тора Горизонтальная проекция линии представляет собой две кривые четвертого порядка.

3. Определение видимости.

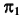
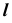
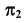
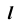
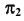
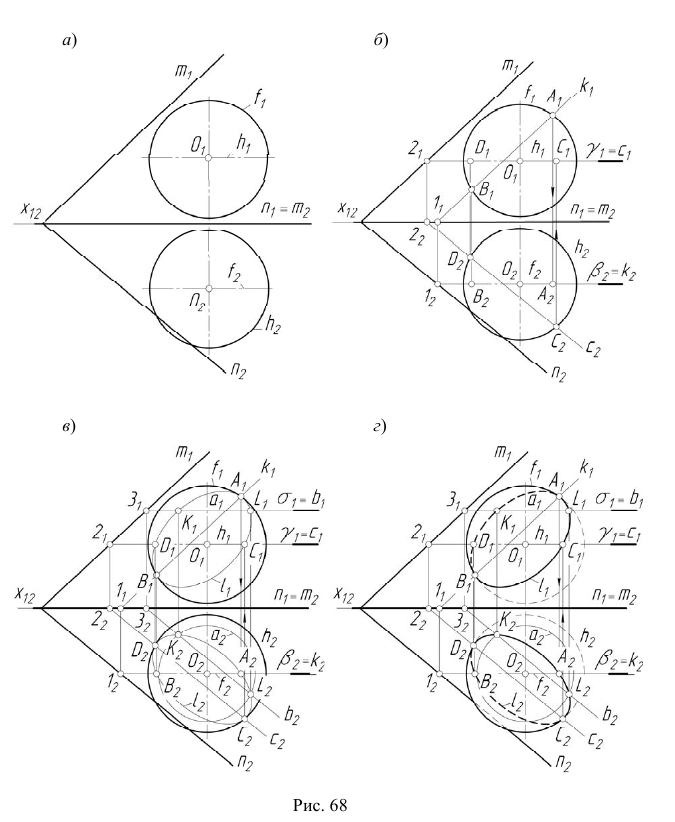
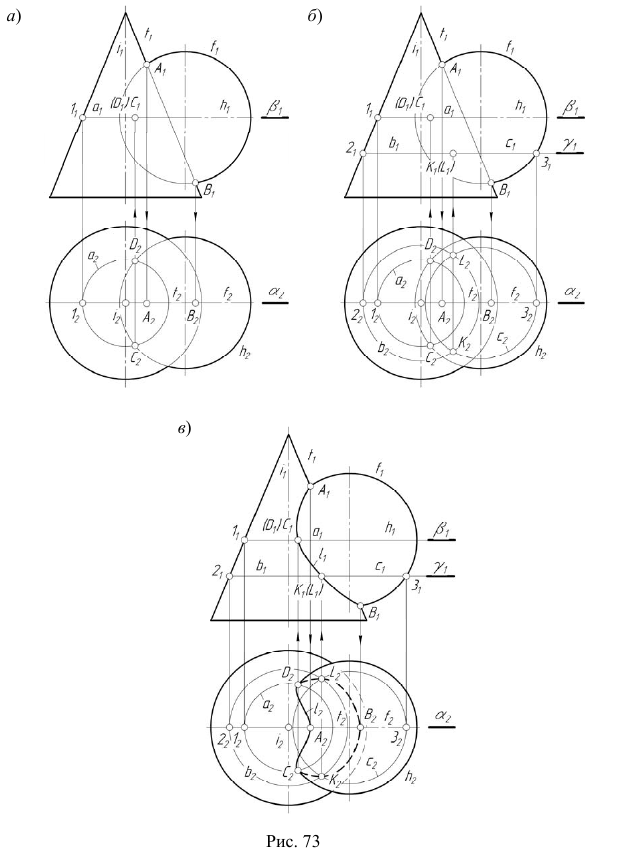
При проецировании на плоскость видимая и невидимая части линии совпадают. Видимость при проецировании на горизонтальную плоскость проекций ограничивает цилиндр. Поэтому видимость линии при проецировании на плоскость проекций определится, например, положением точки A. Точка A при- надлежит видимой части цилиндра, следовательно, часть линии от точки A до контурной линии цилиндрической поверхности — видимая. В поле проекций этот участок отмечен сплошной основной линией.

Пересечение поверхностей общего положения. Способ вспомогательных концентрических сфер

В качестве первого примера рассмотрим решение задачи на основе способа секущих плоскостей.

Задача:

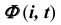
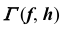
На эпюре Монжа построить проекции линии пересечения конической поверхности со сферой (рис. 72).

Вначале определим характер линии пересечения этих поверхностей и ее проекций. Две поверхности второго порядка пересекаются в общем случае по кривой четвертого порядка. Горизонтальная проекция искомой линии 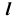будет представлять собой кривую четвертого порядка. Фронтальная же проекция будет являться кривой второго порядка на основании следующей теоремы: если две поверхности порядка n и m имеют общую плоскость симметрии, то линия их пересечения прямоугольно проецируется на эту плоскость или ей параллельную в кривую порядка (n×m)/2.

Для решения этой задачи в качестве вспомогательных плоскостей используются плоскости уровня, параллельные 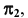так как одна из проекций линии пересечения такой плоскости с заданными поверхностями представляет собой прямую, а вторая — окружность.

Алгоритм решения

1. Определим проекции точек изменения видимости линии 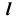(рис. 73, а).

а) Строим проекции точек A и B, используя в качестве вспомогательной плоскость

б) Строим проекции точек С и D, используя в качестве вспомогательной плоскости плоскость уровня

2. Определим произвольные общие точки (K и L) заданных фигур, используя в качестве вспомогательной плоскости плоскость уровня 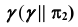(рис. 73, б):

Для построения других точек искомой линии 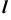повторим последовательность построений п. 2 данной задачи.

3. Определим видимость линии

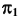
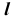
При проецировании на плоскость видимая и невидимая части линии совпадают, так как общая плоскость симметрии поверхностей параллельна фронтальной плоскости проекций.

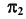
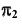
Видимость при проецировании на горизонтальную плоскость проекций ограничивает сфера. Поэтому видимость линии на определится, например, положением точки A. Точка A принадлежит видимой части сферы, следовательно, часть линии от точки C до точки D, содержащая точку A, — видимая. В поле проекций этот участок отмечен сплошной основной линией (рис. 73, в).

В качестве второго примера рассмотрим решение задачи на основе способа вспомогательных концентрических сфер.

Способ вспомогательных концентрических сфер

Способ вспомогательных концентрических сфер основан на следующем определении: две соосные поверхности вращения пересекаются по окружностям, плоскости которых перпендикулярны оси вращения 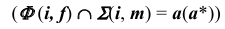(рис. 74, а).

Этот способ применяется только для определения линии пересечения поверхностей вращения, оси вращения которых пересекаются, а общая плоскость симметрии должна быть плоскостью уровня. В этом случае вспомогательные сферы с центрами в точке пересечения осей вращения заданных поверхностей пересекают обе поверхности по окружностям, которые проецируются в виде прямых на плоскость, параллельную общей плоскости симметрии (рис. 74, б).

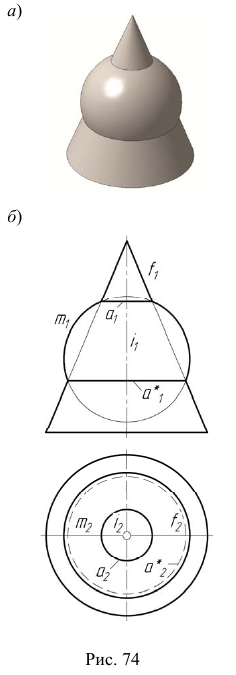
Задача:

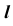
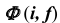
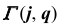
На эпюре Монжа построить проекции линии пересечения поверхности с поверхностью (рис. 75, а).

Вначале определим характер линии пересечения этих поверхностей и ее проекций. Две поверхности второго порядка пересекаются в общем случае по кривой четвертого порядка, поэтому горизонтальная проекция искомой линии 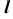будет представлять собой кривую четвертого порядка. Фронтальная же проекция будет представлять собой кривую второго по- рядка, так как поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций.

Для определения общих точек поверхностей будем пересекать их сферами с центрами в точке пересечения осей вращения этих поверхностей

Алгоритм решения

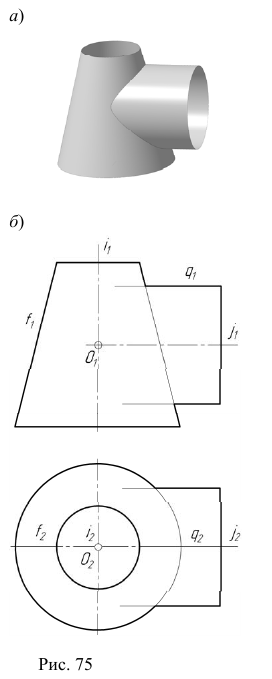
Общая плоскость симметрии заданных поверхностей параллельна фронтальной плоскости проекций (рис. 75, б), поэтому решение задачи начнем с построения фронтальных очерков вспомогательных сфер.

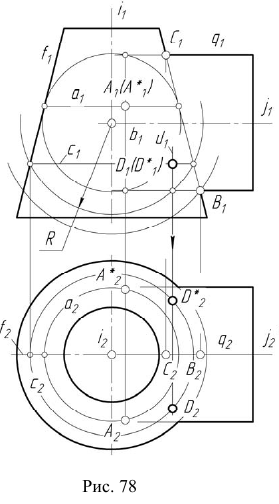
1. Строим фронтальный очерк сферы наименьшего радиуса. Сферой наименьшего радиуса 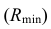является сфера, касательная к одной из поверхностей и пересекающая другую. На эпюре Монжа этой сфере соответствует окружность, касательная очерковых прямых конической поверхности (рис. 76).

Сфера касается конической поверхности по окружности 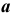и пересекает цилиндрическую поверхность по окружности b. При этом плоскости окружностей а и b перпендикулярны осям вращения i и j соответственно.

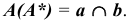
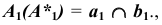
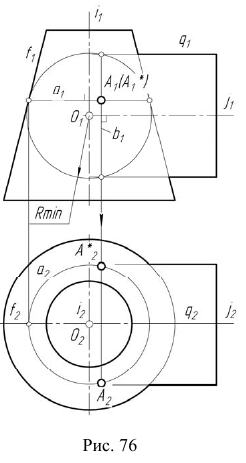
Первая пара общих точек поверхностей определится на пересечении этих окружностей — Фронтальные проекции общих точек определятся на пересечении отрезков прямых — а горизонтальные проекции — по условию принадлежности конической поверхности, т.е.

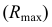
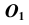
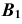
2. Строим фронтальный очерк сферы наибольшего радиуса. Радиусу наибольшей сферы на фронтальной проекции соответствует расстояние от точки до наиболее удаленной точки пересечения очерков заданных поверхностей (рис. 77).

3. Строим фронтальный очерк сферы произвольного радиуса из диапазона 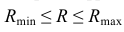(рис. 78).

Сфера радиуса R пересекает коническую и цилиндрическую поверхности по окружностям с и d соответственно. На пересечении этих окружностей определится еще одна пара общих точек заданных поверхностей:

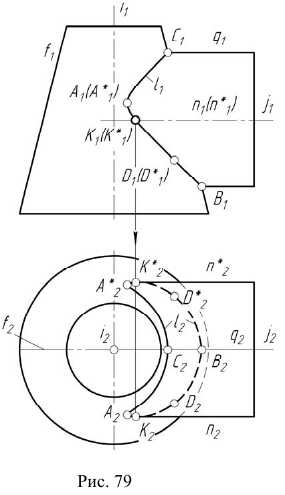
Для построения других точек искомой линии 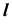повторим последовательность построений п. 3 данной задачи.

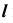
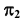
4. Определим проекции точек изменения видимости линии при проецировании на плоскость (рис. 79).

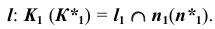
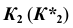
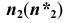
Отметим фронтальные проекции точек изменения видимости линии Горизонтальные проекции будут принадлежать соответствующим горизонтальным очерковым прямым цилиндрической поверхности.

5. Определим видимость линии

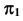
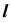
При проецировании на плоскость видимая и невидимая части линии совпадают, так как общая плоскость симметрии поверхностей параллельна фронтальной плоскости проекций.

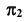
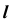
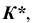
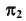
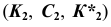
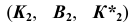
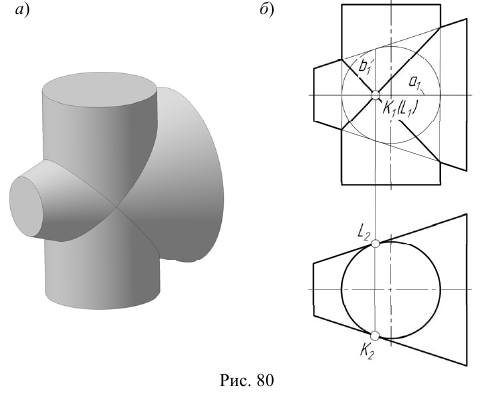
Видимость при проецировании на горизонтальную плоскость проекций ограничивает цилиндр. Поэтому видимость линии на определится, например, положением точки C. Точка C принадлежит видимой части сферы, следовательно, часть линии от точки K до точки содержащая точку C, — видимая. В поле проекций этот участок отмечен сплошной основной линией (рис. 79), а участок — штриховой.

Частные случаи пересечения поверхностей вращения второго порядка

К поверхностям второго порядка относятся линейчатые поверхности вращения, а также поверхности, образованные вращением кривой второго порядка вокруг оси симметрии этой кривой.

Теорема Монжа

Если две поверхности второго порядка вписаны в третью поверхность второго порядка или описаны вокруг нее, то линия их пересечения распадается на две кривые второго порядка.

На рис. 80, а изображены цилиндрическая и коническая поверхности вращения, описанные вокруг сферы.

Цилиндрическая и коническая поверхности касаются сферы по окружностям 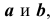которые пересекаются в точках K и L. Через эти точки и будут проходить линии пересечения рассматриваемых поверхностей (рис. 80, б).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник