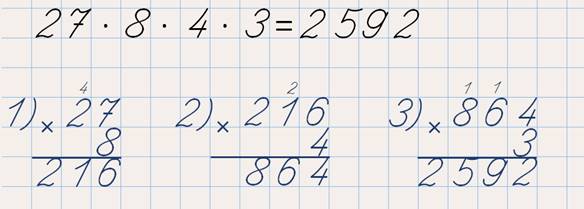Что такое перестановка множителей
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 52. Переместительное свойство умножения
Перечень вопросов, рассматриваемых в теме:
Компоненты умножения: первый множитель, второй множитель.
Результат умножения – произведение.
Переместительное свойство умножения – от перестановки мест множителей произведение не изменяется. В общем виде переместительное свойство умножения записывают так: a • b = b • a.
Обязательная литература и дополнительная литература:
Теоретический материал для самостоятельного изучения
Рассмотрите выражения. Выполните вычисления устно, используя таблицу умножения.
Проверьте, 3 • 2= 6, 6 • 4 = 24, 3 • 5 = 15
А теперь в каждом произведении поменяйте множители местами и найдите значение получившихся произведений, заменив их суммой одинаковых слагаемых.
4 • 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24
Множители поменяли местами. Произведения не изменились, они равны в каждой паре равенств.
Это переместительное свойство умножения. Если множители поменять местами, произведение не изменится. Оно записывается так: a + b = b + a.
Составим равенства по рисунку и найдем их значение.
6 • 3 = 18. Так как в каждом ряду 6 яблок одного цвета и таких рядов 3.
3 • 6 = 18. Так как 3 столбца яблок разного цвета и таких столбцов 6.
Получили равные произведения, хотя множители поменяли местами.
Составим равенства к следующему рисунку и найдем значение выражений.
5 • 2 = 10. Так как 2 ряда по 5 треугольников.
2 • 5 = 10. Так как 5 столбцов по 2 треугольника в каждом. Множители поменяли местами. Сравним произведения. Они одинаковые.
Составим равенства к этому рисунку.

На рисунке 2 ряда вазочек, по 3 вазочки в каждом. Получаем равенство.
А можем рассуждать по-другому. 3 столбца вазочек, по 2 вазочки в столбце. Составляем равенство. 2 • 3 = 6. Множители поменяли местами. Произведения не изменились.
Решим задачу. В школьном саду 3 ряда кустов малины, по 6 кустов в каждом ряду. Сколько всего кустов малины в школьном саду?
Для решения выбираем действие умножение, так как неизвестно общее число кустов.
Сравним с решением другой задачи.
В школьной столовой 6 рядов столов, по 3 стола в каждом ряду. Сколько всего столов в школьной столовой?
Для решения задач выбрали действие умножение. Множители поменяли местами. Произведения одинаковые.
Но в первой задаче большее число умножали на меньшее. А во второй задаче, наоборот, меньшее на большее. В математике удобнее большее число умножать на меньшее. Для этого используют переместительное свойство умножения.
Переместительное свойство умножения – полезное правило, не сложное для запоминания. Свойство позволяет выбирать более удобный способ умножения чисел.
Ответим на вопрос, поставленный в начале урока.
От перестановки множителей произведение не меняется. Это переместительное свойство умножения. В общем виде оно записывается так:
Переместительное свойство умножения используется для удобства вычислений.
Выполним несколько тренировочных заданий.
1. Используя переместительное свойство умножения, найдите значение второго выражения в каждой паре, зная значение первого.
В каждой паре значения выражений будут одинаковыми, так как множители поменяли местами.
Перестановка и группировка множителей
Урок 34. Математика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Перестановка и группировка множителей»
А вы знаете, ребята, оказывается, в числовых выражениях, состоящих из нескольких множителей, числа могут прыгать, меняться местами, становиться парами. В общем, делают то, что им удобно.
И я сейчас расскажу вам о том, как можно выполнять перестановку и группировку множителей в числовых выражениях для того, чтобы удобно было находить их значения.
Но сначала давайте вспомним свойства умножения.
35 · 9 · 2 = 35 · 2 · 9
Вы догадались, какое это свойство? Конечно, переместительное! Для удобства вычисления множители переставили, поменяли местами.
А вот сейчас какое свойство применяется?
26 · 8 · 5 = 26 · (8 · 5)
Я думаю, что вы помните – это сочетательное свойство. Для удобства вычисления два соседних множителя заменили их произведением. То есть, как бы сгруппировали эти множители.
А сейчас я хочу показать вам вот такое числовое выражение:
Видите, в этом выражении только перестановки или только группировки множителей недостаточно для того, чтобы выполнить вычисление легко, без затруднений. Здесь нужно применить оба эти свойства умножения.
Так-так, надо подумать. Двадцать пять на четырнадцать умножать совсем неудобно. Если двадцать пять умножать на пять – тоже не очень удобное для дальнейшей работы число получится – сто двадцать пять.
А вот если двадцать пять умножить на четыре, получится сто. А любое число умножить на сто очень просто. И при умножении четырнадцати на пять тоже получится круглое число – семьдесят. Поэтому, переставив числа вот в таком порядке и сгруппировав их, мы получим числовое выражение, значение которого легко найти, выполнив вычисления в уме.
25 · 14 · 5 · 4 = (25 · 4) · (14 · 5) = 100 · 70 = 700
Правда, ведь так вычислять гораздо удобнее?
А теперь посмотрим вот на такое числовое выражение:
Я надеюсь, вы уже поняли: для того, чтобы умножение выполнить без особых затруднений, надо переставить и сгруппировать множители так, чтобы результаты в скобках были круглыми числами. Или хотя бы один из результатов.
Чтобы круглым получилось произведение с числом девятнадцать, вторым множителем может быть только число десять. И при умножении пятнадцати на четыре тоже получится круглое число. Это нам и надо.
10 · 15 · 4 · 19 = (10 · 19) · (15 · 4) = 190 · 60 = 11 400
Выполняем перестановку и группировку. Первое произведение равно ста девяноста, второе – шестидесяти. Перемножаем эти числа. Произведение равно одиннадцати тысячам четырёмстам.
А теперь попробуйте сами найти значение вот этих числовых выражений удобным способом.
Ну что, справились с заданием? Не всё получилось? Давайте проверять.
В первом выражении можно переставить и сгруппировать множители вот так:
9 · 6 · 5 · 3 = (9 · 3) · (6 · 5) = 27 · 30 = 810
При этом во второй скобке получается круглое число, и мы без особого труда умножим двадцать семь на тридцать.
Во втором выражении удобнее переставить и сгруппировать множители вот так:
2 · 10 · 35 · 8 = (2 · 35) · (10 · 8)
2 · 10 · 35 · 8 = (10 · 8) · (2 · 35)
На результат в данных выражениях это не влияет. Выполняем вычисления.
2 · 10 · 35 · 8 = (10 · 8) · (2 · 35) = 80 · 70 = 5 600
И в первой, и во второй скобках получились круглые числа, которые легко перемножить.
45 · 8 · 2 · 4 = (45 · 2) · (8 · 4) = 90 · 32 = 2 880
А вот последнее, четвёртое выражение… Как ни старайся, при решении этого выражения ни перестановка, ни группировка множителей нам не поможет, так как в нём нет ни одной пары множителей, при умножении которых получится круглое число. Так что это выражение надо будет решать, записывая вычисления столбиком.
Ну вот и всё, о чём я сегодня с вами хотела поговорить.
Не забывайте, ребята:
Если числовое выражение состоит из нескольких множителей, можно выполнить перестановку и группировку этих множителей так, чтобы вычисление было удобно выполнять. Такой способ целесообразно применять в том случае, если при умножении хотя бы одной пары множителей получится круглое число.
Ну а теперь я прощаюсь с вами, ребята! Удачной работы!
Урок математики во 2 классе по теме «Перестановка множителей.»
Выбранный для просмотра документ Технологическая карта урока математики по теме «Перестановка множителей».docx
Демонстрационный урок математики во 2-а классе
Технологическая карта урока математики
во 2 классе по теме «Перестановка множителей»
Тема урока : Перестановка множителей.
Цель: создание условий для достижения учащимися образовательных результатов:
— личностных: 1) положительно относиться к школе, учению; проявлять познавательные потребности и учебные мотивы; соблюдать организованность, дисциплинированность на уроке.
2) проявлять к собеседнику внимание и терпение, умение выполнять самооценку своей деятельности.
Познавательные УУД: добывать новые знания, находить необходимую информацию, перерабатывать информацию (анализ, сравнение,)представленную в разных формах.
— предметных: понимать, что такое «переместительное свойство умножения», уметь его применять, закрепить смысл действия умножения, формировать вычислительные навыки устного счета.
знакомство учащихся с переместительным свойством умножения на конкретных примерах;
формировать умение применять его на практике; закрепить смысл умножения;
развитие математической речи на основе использования изучаемой закономерности; развивать вычислительные навыки, мыслительные операции сравнения, классификации;
Методы и формы обучения : Объяснительно-иллюстративный; индивидуальная, фронтальная, парная.
Приемы организации учебной деятельности учащихся: поиск нового знания посредством собеседования и парной работы; самостоятельная работа с педагогическим сопровождением тех учеников, которые в этом нуждаются
Приём: высказывание добрых пожеланий учащимся
-Нас звонок собрал всех в класс,
Урок математики у нас.
Будем думать, рассуждать.
Нам пора урок начать.
Хотите новое узнать? (Да)
Будьте все, внимательны активны и старательны.
— Откройте тетради и запишите число и классная работа.
Высказывают добрые пожелания друг другу.
Записывают дату, вид работы.
Уметь совместно договариваться о правилах поведения общения в школе и следовать им.
-Посмотрите на числовые выражения
-Найдите лишнее выражение.
-Почему вы выбрали именно третье выражение?
-Что общего во всех выражениях?
-Каким действием можно заменить сумму одинаковых слагаемых?
— представьте суммы виде произведения и найдите значения.
— Проверка со слайда (слайд)
-Из чего состоит произведение?
-Что получается в результате действия умножения?
Математика. 4 класс
Конспект урока
Математика, 4 класс
Урок № 40. Перестановка и группировка множителей
Перечень вопросов, рассматриваемых в теме:
— что такое перестановка и группировка множителей?
— какие есть способы перестановки и группировки множителей?
Перестановка – изменение, перемещение порядка следования множителей в записи.
Группировка – объединение множителей для удобного способа вычисления произведения.
Основная и дополнительная литература по теме урока:
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.16
3. Чекин А. Л. Математика. 3 класс. Ч.1. М.: Академкнига/Учебник, 2014. – с.88
Теоретический материал для самостоятельного изучения
Итак, мы знаем, что от перестановки множителей произведение не изменяется.
Это свойство также справедливо для трёх и более чисел. Рассмотрим на примере. Дано произведение трёх множителей 5 • 4 • 2. Вычислим произведение: пять умножим на 4, получится 20, 20 умножим на 2, получится 40.
5 • 4 • 2 = 20 • 2 = 40
Переставим местами в этой записи множители 5 • 2 • 4 и найдем значение этого выражения: 5 умножим на 2, получится 10, 10 умножим на 4, получится 40. Результат не изменился.
Значит, множители в произведении можно переставлять как угодно, результат от этого не изменится.
5 • 2 • 4 = 10 • 4 = 40
При умножении числа на произведение можно сначала число умножить на первый множитель, а полученный результат умножить на второй множитель.
Поменяем местами левую и правую части равенства, а также уберем необязательные скобки в левой части, то второе свойство умножения можно сформулировать по другому. Два соседних множителя можно заменить их произведением.
Это означает, что при вычислении произведения нескольких чисел можно сгруппировать соседние множители и вычислить их произведение с начала.
Посмотрим, как можно использовать эти свойства умножения при вычислении значений выражений. Например, надо узнать произведение трёх чисел 25, 7 и 4. Если выполнять вычисления по порядку, то сначала нам нужно будет 25 • 7. В результате получится трехзначное число. И потом это трехзначное число умножить на 4, что делать гораздо сложнее.
Обрати внимание, что если 25 • 4, то получится 100. Это число, умножать на которое легко и быстро. Поэтому внесем изменения, чтобы произведение чисел 25 • 4 вычислялось первым. Согласно первому свойству умножения, мы можем переставить местами множители 25 и 7. От перестановки множителей произведение не изменится, а затем сгруппировать множители 25 и 4 и вычислить их произведение. Найти произведение чисел 7 и 100 не составит особого труда. Мы легко получаем результат 700.
25 • 7 • 4 = 7 • (25 • 4) = 7 • 100 = 700
Теперь посмотрим, каким образом можно найти произведение четырех чисел 50, 9, 2 и 8, используя знакомые нам свойства умножения.
Используя первое свойство умножения, поменяем местами множители 9 и 2.
Используя второе свойство умножения, сгруппируем соседние множители 50 и 2, а также 9 и 8. Вычислим соответствующие произведения. Теперь мы легко найдем результат, умножив 72 на 100. Получим 7200.
50 • 9 • 2 • 8 = 50 • 2 • 9 • 8 = 100 • 72 = 7200
Задания тренировочного модуля:
1. Вставьте пропущенные числа в решение выражения:
4 • 500 • 6 • 2 = 4 •___ • ___• 2.
Правильный ответ: 500; 2.
2. Распределите математические записи по группам. Перенесите их в соответствующие столбики.
Конспект открытого урока по математике по теме: «Прием перестановки множителей и его использование в вычислениях»
ГУО «Средняя школа №177 г. Минска»
Цель: закрепление умения перестановки множителей и его использования в вычислениях.
1. Формировать умение применять переместительное и другие свойства умножения c помощью решения примеров.
2. Развивать навык логического мышления через решение устных и письменных вычислений, а также названия компонентов при умножении.
3. Закреплять умение находить периметр фигур.
4. Воспитывать уважительное отношение к мнению своих товарищей, интерес к изучению математики.
Оборудование: изображение Карслона, изображения банок с вареньем, карточки с заданиями.
ü стимулирующая – уточняющие вопросы (скажи точнее, подумай)
ü обучающая – объяснение инструкции с показом примера
I .Организационная часть
Здравствуйте, ребята! Посмотрите, кто к нам сегодня прилетел в гости? (Карлсон) Правильно! Из какой сказки этот персонаж? («Малыш и Карслон»)
Карслон прилетел узнать, чему вы научились на математике. Он приготовил для вас задания.
Пусть урок принесёт вам радость! Сядьте красиво, постарайтесь отвечать полными ответами, работать быстро. Учитесь слушать и слышать друг друга. Я уверенна, что вы будете стараться и у вас всё получится.
Покажите, какое у вас настроение в начале урока с помощью наших птичек.
Игра «Карлсон и варенье»
— Карлсон ждал вас в гости, хотел угостить вареньем. Но перепутал все банки и не знает, где какое варенье. Давайте поможем Карлсону. Для этого нужно подобрать к каждому выражению правильное значение.
Примеры записаны на доске. Вам надо решить пример и подобрать банку с решением. Дима, выходи к доске.
— Запишите номера банок в порядке уменьшения. (От большего к меньшему)
74, 60, 52, 43, 39, 37, 25, 21, 8
Ребята, давайте перевернём банки.
— Какое слово получилось? (УМНОЖЕНИЕ)
— Вам знакомо это слово? (Да.)
— Что такое умножение? (Арифметическое действие.)
— Какие ещё арифметические действия вы знаете? (СЛОЖЕНИЕ, ВЫЧИТАНИЕ, ДЕЛЕНИЕ)
2.3.Сообщение темы урока
Что мы делали на прошлом уроке? (Заменяли умножение сложением и наоборот, учились переставлять множители местами)
Давайте повторим правила, которые мы с вами уже знаем. Откройте тетради для правил или посмотрите на доску.
1)Сложение одинаковых слагаемых можно заменить умножением.
2)Умножение двух чисел можно заменить сложением одинаковых слагаемых.
3)От перестановки множителей произведение не меняется.
Сегодня на уроке мы будем снова говорить про умножение. Будем учиться заменять сложение умножением и наоборот и тренироваться переставлять множители местами.
2.4.Работа с учебником
Открываем тетрадь. Записываем число, классная работа.
Открываем учебник. Стр.112,№ 1.
Нам надо вычислить, сколько роз в трех букетах. Сколько цветов в букете? (5)
Мы знаем, что умножение можно заменить сложением одинаковых слагаемых.
Сколько у нас получилось роз? 15.
Теперь нам надо узнать, сколько тюльпанов в 5 букетах.
Сколько получилось тюльпанов? 15.
Мы видим, что 5*3 = 15 и 3*5=15. Тут мы вспоминаем наше правило, что от перестановки множителей произведение не меняется.
Я говорю, до чего вам надо дотронуться, и показываю другую часть тела. Ваша задача делать то, что я говорю, а не то, что показываю. Начали! Дотроньтесь до уха/колена/шеи/живота/локтя/спины/плеча/головы/руки/ноги. Молодцы!
2.6.Задание на карточке
Следующее задание, которое для вас подготовил Карслон. Я вам раздам карточки. Вам надо будет сравнить выражения: поставить знак >,
2.7.Работа с учебником
Вставьте пропущенные числа так, чтобы равенства были верными. Запишите в тетрадь.
Сейчас дадим нашим глазкам немного отдохнуть. Встаньте, возьмите карандаш. Поставьте его перед собой на вытянутой руке. Посмотрите на кончик вашего карандаша, теперь на меня, снова на кончик, снова на меня. Теперь быстро поморгайте, закройте глазки, откройте.
2.9.Задания на карточках
Еще одно задание от нашего Карслона. Посмотрите на карточки. Вам надо заменить сложение умножением. Мы знаем правило, что сложение одинаковых слагаемых можно заменить умножением. Выходим к доске, записываем первый пример.
Еще одна карточка для вас. Тут надо вспомнить другое правило. Умножение двух чисел можно заменить сложением одинаковых слагаемых. Решаем на доске. Ваня первый.
2.10.Задание «Найди периметр»
Посмотрите на доску. Какая эта фигура? (Квадрат) Правильно. Вам надо найти периметр квадрата. Я вам раздам карточки. Вам надо измерить длину сторон. Что мы знаем о квадрате? (Все стороны равны). Сколько сантиметров сторона квадрата? (3 см)
Что такое периметр? (Сумма длин всех сторон)
Как найти периметр этого квадрата? 3см+3см+3см+3см=12см. Сложение одинаковых слагаемых можно заменить чем? (Умножением) 3*4=12 Запишите в тетрадь.
III .Заключительная часть
Давайте вспомним, чем мы сегодня занимались на уроке? Что нового узнали на уроке? Какие задания вам были интересны? Что было трудным на уроке? Открываем дневники, записываем домашнее задание. С.113,№7. Откроем книгу. Вам надо будет начертить квадрат и найти его периметр несколькими способами.
Покажите, какое у вас настроение в конце урока с помощью наших птичек. Молодцы! Урок окончен. Карслон вами доволен!
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Урок–конференция с работой в парах постоянного состава “НАША ФЕРМА». Методическая разработка. (9 класс)
Выступление на педсовете по теме «Нестандартные формы контроля на уроке математике»
Кроссворд по математике «Контроль знаний» (3 класс)
Конспект урока на тему «Деление. Конкретный смысл действия.» «Математика» (2 класс 2 часть М. И. Моро)
Факультатив «Математика без границ» 6 класс
Рабочая программа по математике 5-9 классы
Анализ урока математики 4 класс
Конспект внеклассного мероприятия «Клуб юных математиков»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5424133 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В России стартует пилотный проект по реабилитации детей-инвалидов
Время чтения: 2 минуты
Ученые изучили проблемы родителей, чьи дети учатся в госпитальных школах
Время чтения: 5 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения создает цифровую психологическую службу для школьников
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.