Что такое периметр и площадь треугольника

Периметр и площадь треугольника

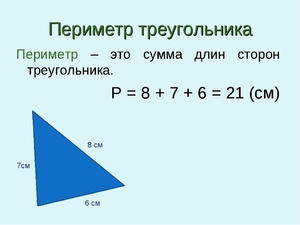
Периметр

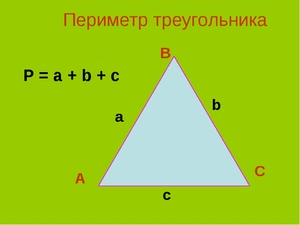
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:

где P — это периметр треугольника, a, b и c — его стороны.

Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:

где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.

Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:

где P — это периметр равностороннего треугольника, a — любая из его сторон.

Площадь

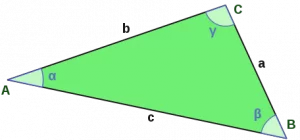
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.

Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна

Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:

Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.

Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.

Общая формула площади треугольника:

где S — это площадь треугольника, a — его основание, h_a — высота, опущенная на основание a.

Источник

Формула треугольника: площадь и периметр

Найти площадь треугольника вы можете, воспользовавшись онлайн-программами, а на этой странице мы ознакомимся с формулами площади и периметра треугольника.

Треугольник – геометрическая фигура, которая состоит из 3 точек, не лежащих на одной прямой, и попарно соединенных 3 отрезками.

Площадь треугольника – это положительная величина, которая характеризует геометрическую фигуру (треугольник) и числовое значение которой выражается квадратными единицами.

Формула площади треугольника

$S = \frac12$

a — сторона треугольника;

h_a — высота, проведенная к стороне а.

a, b — стороны треугольника;

C — угол между сторонами a и b.

Формула Герона

a, b, c — стороны треугольника;

$p= \frac<2>$ — полупериметр.

$S=pr$

$p= \frac<2>$ — полупериметр треугольника;

r — радиус вписанной в треугольник окружности.

a, b, c — стороны треугольника;

R — радиус описанной окружности.

Формула площади равнобедренного треугольника

Равнобедренным называется треугольник, у которого две стороны равны.

a, b — стороны равнобедренного треугольника.

Формула площади равностороннего треугольника

Равносторонним называется треугольник, у которого все стороны равны. Медиана, высота, биссектриса равностороннего треугольника, проведенные с одной вершины — совпадают.

a — сторона равностороннего треугольника.

m — медиана (высота, биссектриса).

R — радиус описанной окружности.

r — радиус вписанной окружности.

Формула площади прямоугольного треугольника

Прямоугольным называется треугольник, если он имеет прямой угол. АС и ВС — катеты, АВ — гипотенуза.

a, b — катеты.

c — гипотенуза;

h_c — высота, проведенная к гипотенузе.

Формула периметра треугольника

Периметр треугольника равен сумме длин всех его сторон (a, b, c).

$P=a+b+c$

P — периметр;

a, b, c — стороны треугольника.

Источник

Формулы определения периметра, площади и сторон треугольника

Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.

Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.

Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:

Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.

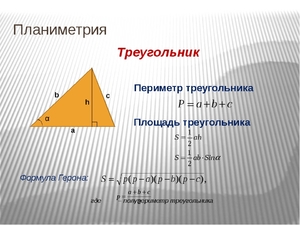
Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:

Из этого видео вы узнаете, как найти площадь треугольника.

Классификация треугольников

Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.

Описание

Чтобы описать любой треугольник, достаточно указать:

Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:

Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.

Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.

Примеры

Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.

Видео

Это видео поможет вам закрепить полученные знания.

Источник

Площадь и периметр треугольника

Треугольник это геометрическая фигура (многоугольник), ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех отрезков.

Периметр

Периметр треугольника равняется сумме всех его сторон: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.

Расчет периметра

Площадь треугольника

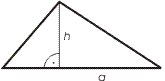
1. Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площдаь, a – основание, h – высота.

2. Вторая формула для расчета площади: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)

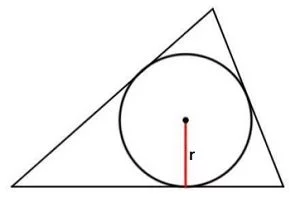
Расчет:

3. Площадь треугольника по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.

4. Формула Герона или площадь треугольника по его трем сторонам: S = √ p · (p — a)(p — b)(p — c) ,
где a, b и c это стороны треугольника и p – половина периметра треугольника.

Источник

Площадь треугольника

Определение площади треугольника

Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.

Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.

Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.

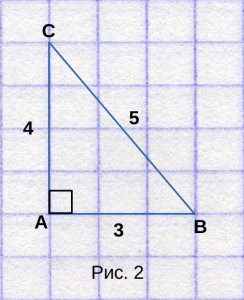
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.

Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.

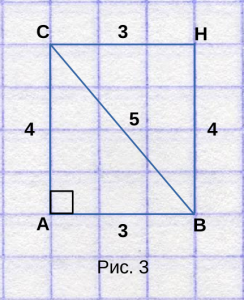
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.

Как видим, весь прямоугольник занимает 12 полных клеток.

Формула площади прямоугольника равна произведению
одной стороны на другую — ​ \( S = ab \) ​,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.

Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: ​ \( S = \frac<1>2 ab \) ​.
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.

Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.

Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.

Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.

Формулы площади треугольника

Ⅰ. Через высоту и основание

a — сторона, на которую падает высота,
b — высота.

Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.

Ⅱ. Через все стороны и периметр

p — полупериметр, вычисляется по формуле: ​ \( p = \frac <2>\) ​,
a, b, c — стороны треугольника.

Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.

Эту формулу площади также называют формулой Герона.

Ⅲ. Через две стороны и угол между ними

\[ S = \frac<1> <2>a \cdot b \cdot \sin β \]

a, b — стороны между которыми расположен угол β,
sin β — синус угла β.

Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.

Ⅳ. Через периметр и радиус вписанной окружности

r — радиус вписанной окружности,
P — периметр треугольника.

Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.

Ⅴ. Через все стороны и радиус описанной окружности

abc — произведение всех сторон треугольника,
R — радиус описанной окружности.

Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.

Ⅵ. Через сторону и два прилежащих к ней угла

a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.

Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.

Источник