Что такое периметр квадрата что такое площадь квадрата

Как найти площадь и периметр квадрата

О том, что такое квадрат, многие помнят из школьного курса. Этот четырехугольник, который является правильным, имеет абсолютно равные углы и стороны. Оглянувшись вокруг, можно заметить, что нас окружает множество квадратов. Каждый день мы сталкиваемся с ними, и порой возникает необходимость найти площадь и периметр этой геометрической фигуры. Вычисление этих значений не принесет труда, если уделить несколько минут времени для просмотра данного видео урока, объясняющего простые правила проведения расчетов.

Обучающее видео “Как найти площадь и периметр квадрата”

Что необходимо знать о квадрате?

Прежде чем приступать к проведению вычислений, необходимо знать некоторые важные сведения об этой фигуре, среди которых:

Как найти площадь квадрата?

Вычисление площади данной фигуры можно просто и легко объяснить на примере:

Как найти периметр квадрата?

Зная, что все стороны данного прямоугольника равны, необходимо сделать следующие манипуляции, чтобы вычислить его периметр:

Все формулы и исчисления, приведенные в рамках данной статьи, применимы для любого прямоугольника. Важно помнить, что когда речь идет о других прямоугольниках, которые не являются правильными, значение сторон будет разным, например 4 и 8 метров. Это означает, что для нахождения площади такого прямоугольника необходимо будет умножать разные по значению стороны фигуры, а не одинаковые.

Необходимо помнить и то, что площадь измеряется в квадратных, а периметр в простых метрах. Если периметр нарисовать в виде одной длинной линии, то его значение не изменится, что говорит о том, что исчисления проводятся в одномерном пространстве.

Площадь измеряется в двухмерном пространстве, о чем говорят квадратные метры, которые мы получаем, умножив метры на метры. Площадь является индикатором наполненности геометрической фигуры, и говорит нам о том, сколько воображаемого покрытия необходимо для того чтобы заполнить квадрат или другой прямоугольник.

Простые объяснения видео урока позволят быстро вычислить площадь и периметр не только квадрата, но и любого прямоугольника. Данные знания школьного курса будут полезны во время ремонта дома или на садовом участке.

Источник

Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a

S=a 2

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L= 2πd

L – длина окружности

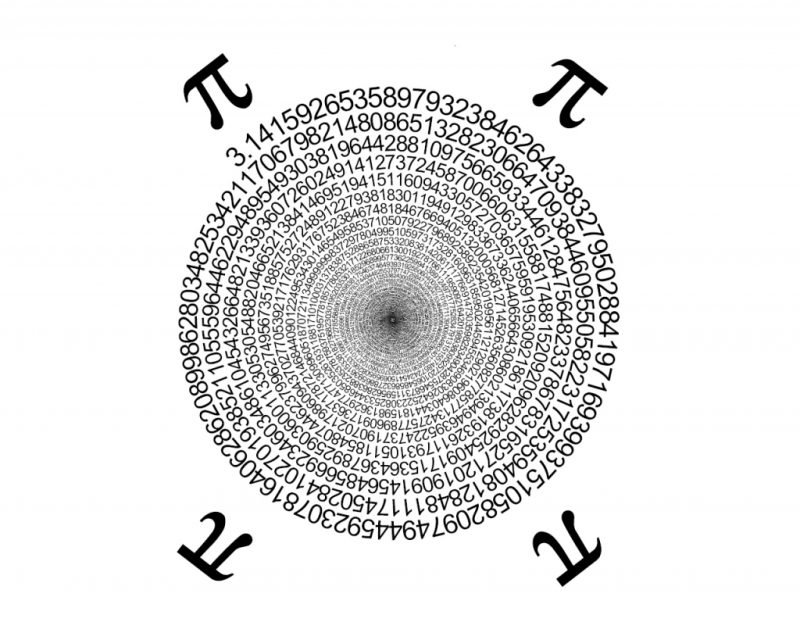
π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Источник

Квадрат, свойства и формулы, площадь и периметр

Квадрат, свойства и формулы, площадь и периметр.

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат (понятие, определение), диагональ квадрата:

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат – это четырехугольник, имеющий равные стороны и углы.

Все углы квадрата прямые. Каждый из них прямой и равен 90°.

Таким образом, все квадраты отличаются друг от друга только длиной стороны.

Рис. 2. Квадрат и диагонали квадрата

Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.

Квадрат – это равносторонний прямоугольник.

Квадрат – это ромб с прямыми углами.

Свойства квадрата:

1. Длины всех сторон равны.

2. Противоположные стороны квадрата параллельны.

3. Все углы квадрата прямые. Каждый из них равен 90°.

4. Сумма углов квадрата равна 360 градусам.

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

5. Диагонали квадрата равны между собой.

6. Диагонали квадрата взаимно перпендикулярны.

7. Диагонали квадрата точкой пересечения делятся пополам.

8. Угол между диагональю и стороной квадрата равен 45 градусам.

9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.

11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Формулы квадрата. Площадь квадрата. Периметр квадрата:

Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.

Формула диагонали квадрата:

, , , , .

Формула радиуса вписанной окружности квадрата:

Радиус вписанной окружности квадрата равен половине его стороны.

.

Формула радиуса описанной окружности квадрата:

.

Формула периметра квадрата:

, , .

Формула площади квадрата:

, , , , .

Источник

Квадрат. Периметр и площадь квадрата.

Рассмотрим фигуру она называеться квадрат.

Стороны AB, BC, CD, DA другое название они имеют ребра; углы A, B, C, D; второе название вершины, зеленим цветом обозначаются диагонали AD, BC. Диагонали в квадрате равны и точкой пересечения делятся пополам.

Периметр P=4•a, Площадь S=a·а

Свойства квадрата

1. Длины сторон квадрата равны.

2. Все углы квадрата прямые.

3. Противолежащие стороны квадрата параллельны друг другу AB∥CD,BC∥AD

4. Сумма всех углов квадрата равна 360 градусов ∠ABC+∠BCD+∠CDA+∠DAB=360​∘​​

5. Величина угла между диагональю и стороной равна 45 градусов ∠BAC=∠BCA=∠CAD=∠ACD=45​∘​​

6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.

7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.

8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.

Поделись с друзьями в социальных сетях:

Источник

Как определить площадь квадрата

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Формула нахождения площади квадрата

Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения площади:

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

Источник