Что такое периметр трапеции
Как найти периметр трапеции
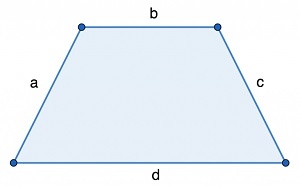
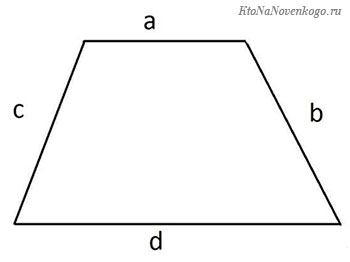
Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.
Периметр трапеции — это сумма длин всех его сторон.
Основные свойства трапеции
Свойства равнобедренной трапеции
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы нахождений периметра
Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.
По всем сторонам
Формула для нахождения периметра выглядит так:
где a, b, c, d — стороны трапеции.
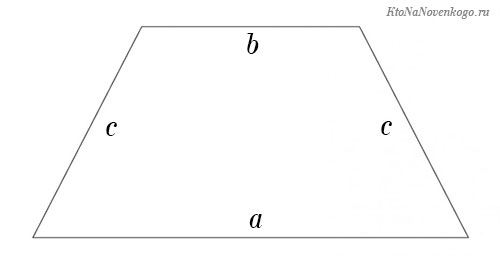
По сторонам равнобедренной трапеции
Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:
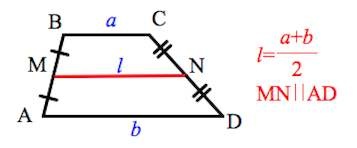
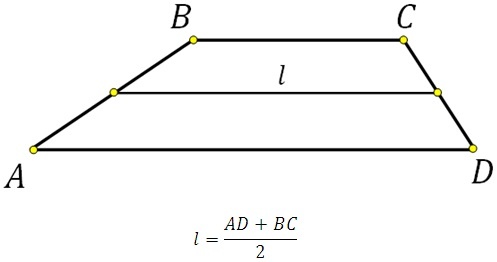
Через среднюю линию
Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:
где l — средняя линия фигуры.
Примеры решения задач
Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.
Задача 1
Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.
Решение:
Нам пригодится самая первая формула для расчета:
Подставляем значения и получаем:
Задача 2
Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.
Решение:
Так как трапеция равнобедренная, удобнее всего будет использовать формулу:
Таким образом, получается:
Задача 3
Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.
Нахождение периметра трапеции: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.
Формула вычисления периметра
Периметр (P) трапеции равняется сумме длин всех ее сторон.
P = a + b + c + d
Периметр равнобедренной трапеции
В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:
P = 2a + b + d или P = 2с + b + d
Периметр прямоугольной трапеции
Для расчета периметра используется такая же формула, что и для разносторонней трапеции.
P = a + b + c + d
Примеры задач
Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.
Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.
Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.
Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.
Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1, d2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
Найти периметр трапеции

| a = |
| b = |
| c = |
| d = |
Вводить можно числа или дроби (-2.4, 5/7, …).
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD – BC |
| 2 |
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| ( a + b ) sin α |
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Формулы определения длины высоты равнобедренной трапеции:
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с 2 – (((а – в) 2 + с 2 – d 2 )/(2(а – в))) 2 ). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с 2 – (а – в) 2 /4). Номер 2.
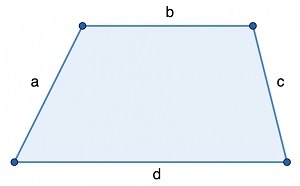
Периметр произвольной трапеции
[ LARGE P_
где:
P – периметр трапеции
a, b, c, d – стороны трапеции
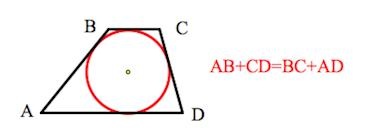
Вписанная окружность
Если в трапецию вписана окружность с радиусом 



Решение задач о прямоугольной трапеции
Задача Даны три стороны, одна из которых перпендикулярная боковая.
Допустим, нам дана прямоугольная трапеция АВСД, у которой АВ перпендикулярно ВС. Известно, что АВ = 12 см, ВС = 1 см, АД = 6 см. Необходимо найти большую боковую сторону.
Из точки С опускаем проводим высоту СК и получаем прямоугольный треугольник СДК и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны СК = АВ = 12 см, а АК = ВС = 1 см.
Находим отрезок КД:
Согласно теореме Пифагора:
Задача Даны оба основания и угол при основании
Дана трапеция АВСД, у которой основания ВС и АД равны 6 и 10 см соответственно, угол ВАД – прямой, а СДА равен 45 градусов. Найдите меньшую боковую сторону.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Формула определения радиуса вписанной в трапецию окружности
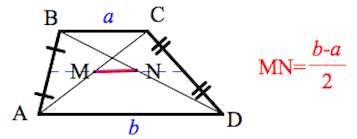
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Определение периметра прямоугольной трапеции
Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:
Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.
Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:
Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
н = (d1 2 * sin γ) / (а + в) или н = (d1 2 * sin δ) / (а + в). Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d1 2 * sin γ) / 2m или н = (d1 2 * sin δ) / 2m. Номер 6а.
Периметр – это границы измерений
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы подробно расскажем, что такое ПЕРИМЕТР, как он считается и каково его практическое применение.
Материал этот изучают в начальных классах школы, но далеко не всегда получается понятно объяснить простые вещи.
Что такое периметр
Периметр – это общая граница любой плоской геометрической фигуры. Измеряется в тех же величинах, что и стороны многоугольников.
У окружности тоже есть периметр. Хотя само слово в этом случае не применяют, говоря – длина окружности. Интересно, что само слово ПЕРИМЕТР изначально и обозначало окружность.
Так оно переводится с древнегреческого «περίμετρον». Но другой, более общий перевод – «измеряю вокруг», и тогда он подходит под все плоские геометрические фигуры как окружность, так и многоугольники.
Расчет периметра многоугольников
Считать периметр многоугольников очень просто. Надо всего лишь сложить длины всех сторон. И неважно, насколько замысловато выглядят сами фигуры.
Рассмотрим периметры самых популярных фигур.
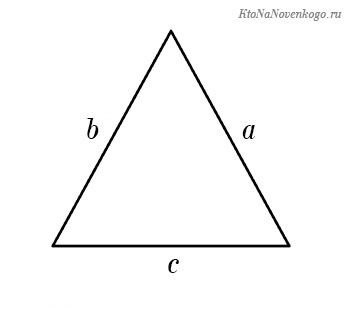
Периметр треугольника
Как мы уже сказали, для расчета периметра треугольника надо просто сложить все его стороны.
Периметр обозначается латинской буквой «P». Он будет равен:
А если треугольник равносторонний или как его еще называют – правильный, то формула заметно упрощается.
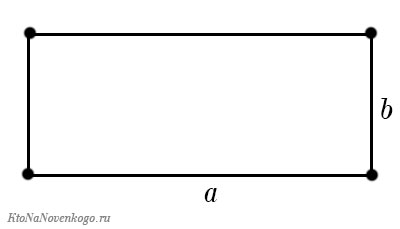
Периметр прямоугольника
Отличительная черта прямоугольника – его противоположные стороны равны.
P = a + b + a + b = 2a + 2b = 2 (a + b)
Как и у треугольника, у прямоугольника есть частный случай, когда всего его стороны равны между собой. И всем известно, что называется такая фигура – квадрат.
Периметр параллелограмма
Если кто забыл, то параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны между собой.
И периметр у него считается точно так же, как и у прямоугольника. Более того, прямоугольник – это частный случай параллелограмма.
P = a + a + b + b = 2a + 2b = 2 (a + b)
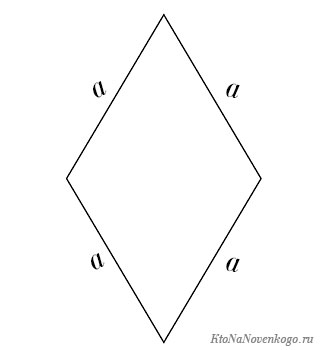
У параллелограмма есть еще один частный случай. Фигура, у которой все стороны равны. И называется она – ромб.
Его периметр считается точно так же, как и у квадрата.
Периметр трапеции
И еще одна фигура, которая частенько встречается в жизни. И ее изучению посвящены отдельные главы школьной программы. Трапеция – это четырехугольник, у которого только две стороны лежат на параллельных прямых.
Но есть и частный случай, который называется равнобедренной трапецией. У этой фигуры непараллельные стороны равны между собой и идут под одинаковым наклоном.
P = a + b + c + c = a + b + 2c
Расчет длины окружности
Для расчета длины окружности, которая, по сути, и является периметром фигуры, есть своя формула. Вот только эту величину, в отличие от многоугольников, принято обозначать латинской буквой «L».
В этой формуле букой r обозначается радиус окружности, то есть расстояние от ее центра до границы. А буква π – это математическая постоянная, которая равна 3,14 (хотя на самом деле число знаков после запятой бесконечно).
Вместо заключения
Для чего в жизни нужно знать про ПЕРИМЕТР? Приведем самый простой пример.
Если вы на даче соберетесь поставить забор, вам нужно будет точно знать, сколько материала покупать. Для этого вы измерите свой участок по длине и ширине. Как правило, дачные участки имеют форму прямоугольников. Соответственно, после этого легко будет посчитать периметр:
где L – длина участка, а W – ширина. И уже с этими расчетами вы можете смело ехать в строительный магазин.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Не только это. Термин «периметр» весьма распространен в силовых структурах. Например: «Прапорщик Савельев отвечает за охрану периметра А, сержант Николаев — за периметр Б». То есть — какой-то ограниченный сектор с особым режимом, находящийся под сигнализацией и т.д.
Каков периметр и площадь трапеции?
Периметр трапеции это сумма длин его четырех сторон. Если одна или несколько длин неизвестны, вы можете иногда использовать теорему Пифагора, чтобы найти ее. Пример: Найдите площадь и периметр показанной трапеции.
Кроме того, каковы стороны трапеции?
Что такое формула периметра?
Периметр, площадь и объем
Также знать Как найти периметр? Пояснение: Чтобы найти периметр прямоугольника, сложите длины четырех сторон прямоугольника. Если у вас есть только ширина и высота, вы можете легко найти все четыре стороны (каждая из двух сторон равна высоте, а две другие стороны равны ширине).
Периметр расстояние по краю фигуры. Узнайте, как найти периметр, сложив длины сторон различных форм.
Может ли трапеция иметь 3 равные стороны?
Какова формула среднего сегмента трапеции?
Как выглядит трапеция?
Как найти периметр с учетом площади?
Что означает периметр в математике?
Периметр расстояние вокруг внешней части формы. Площадь измеряет пространство внутри фигуры. Узнайте, как рассчитать периметр и площадь для различных форм. Создал Сал Хан.
Что такое пример периметра?
Периметр общая длина сторон двухмерной фигуры. … Другие примеры могут включать определение общей длины границы футбольного поля или длины вязания крючком или ленты, необходимой для покрытия границы коврика для стола.
Как найти периметр недостающей стороны?
Чтобы найти недостающую длину стороны, напишите дополнительное предложение для периметра треугольника. Периметр треугольника равен сумме длин всех его сторон. Добавьте длины сторон, которые вам известны. Найдите длину стороны, при которой сложение будет верным.
Что такое пример периметра?
Периметр снаружи или внутри?
Может ли трапеция иметь равные стороны?
У трапеции равные стороны?
| Трапеция | трапеция | |
|---|---|---|
| В Соединенном Королевстве: | НЕТ параллельных сторон | пара параллельных сторон |
Есть ли у трапеции четыре равные стороны?
Трапеции имеют только одну пару параллельных сторон; параллелограммы имеют две пары параллельных сторон. Трапеция никогда не может быть параллелограммом. … Трапеции четырехсторонние многоугольники, поэтому все они четырехугольники.
Может ли трапеция иметь 4 прямых угла?
Ответ проверен экспертом Это невозможно. Поскольку трапеции являются четырехугольниками, сумма их углов должна составлять 360. Если три угла являются прямыми углами (по 90 градусов каждый), то единственным возможным измерением последнего угла будет 90 градусов, что составляет четвертый прямой угол.
Какой угол у трапеции?
Пояснение: Сумма внутренних углов всех четырехугольников равна 360°. У равнобедренных трапеций два верхних угла равны друг другу. Точно так же два нижних угла также равны друг другу.
Все ли стороны совпадают на трапеции?
Может ли трапеция иметь 3 прямых угла?
У трапеции не может быть трех прямых углов.
Сумма четырех внутренних углов любого четырехугольника всегда составляет 360 градусов. …