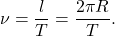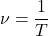Что такое период движения в физике определение
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Разница векторов есть 

Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью 
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Характеристики колебаний
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
\( \large T \left( c \right) \) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Что такое частота
Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
\( \large \nu \left( \frac<1>
Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1>
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
\( \large \displaystyle \omega \left( \frac<\text<рад>>
Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».
Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.
Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>
И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).
\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.
Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]
Из графика следует, что период T = 4 сек.
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
Для этого используем формулу:
\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)
Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».
Примечания:
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.
Как на графике колебаний отметить фазу
На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
\( \large \varphi_<01>\) – для первого процесса и,
\( \large \varphi_<02>\) – для второго процесса.
Определим разность фаз между первым и вторым колебательными процессами:
Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);
\( \large N \left( \text <шт>\right) \) – количество полных колебаний;
\( \large t \left( c \right) \) – общее время для нескольких колебаний;
\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.
\(\large \displaystyle \omega \left( \frac<\text<рад>>
\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;
\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;
\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
период движения
Смотреть что такое «период движения» в других словарях:
период движения — period of motion Наименьший промежуток времени или другой независимой переменной, после которого движение повторяется. Шифр IFToMM: 2.2.46 Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ДВИЖЕНИЯ ТЕКТОНИЧЕСКИЕ — механические (в основном) перемещения в земной коре и в верхней мантии (тектоносфере), вызывающие изменение структуры геол. теч. Д. т. обычно отражаются в рельефе земной поверхности. Они связаны с физико хим. процессами, происходящими на разных… … Геологическая энциклопедия
Период (определ. круг времени) — Период (от греч. períodos обход, круговращение, определённый круг времени), 1) промежуток времени, в течение которого совершается какой либо процесс. 2) Этап общественного развития, общественного движения. См. также Период в музыке, Период в… … Большая советская энциклопедия
ПЕРИОД — (от греческого periodos обход, круговращение, определенный круг времени), 1) промежуток времени, охватывающий какой либо законченный процесс. 2) Этап общественного развития, общественного движения … Современная энциклопедия
ПЕРИОД — (от греч. periodos обход круговращение, определенный круг времени), 1) промежуток времени, охватывающий какой либо законченный процесс.2) Этап общественного развития, общественного движения … Большой Энциклопедический словарь
ПЕРИОД ГРАФИКА — время занятия перегона парой поездов или группой чередующихся поездов, характерной для разных типов графика (парного, непарного, пачечного, пакетного). П. г. однопутной линии (фиг. 1) состоит из суммы времени занятия перегона в обоих направлениях … Технический железнодорожный словарь
период движения
Смотреть что такое «период движения» в других словарях:
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ДВИЖЕНИЯ ТЕКТОНИЧЕСКИЕ — механические (в основном) перемещения в земной коре и в верхней мантии (тектоносфере), вызывающие изменение структуры геол. теч. Д. т. обычно отражаются в рельефе земной поверхности. Они связаны с физико хим. процессами, происходящими на разных… … Геологическая энциклопедия
Период (определ. круг времени) — Период (от греч. períodos обход, круговращение, определённый круг времени), 1) промежуток времени, в течение которого совершается какой либо процесс. 2) Этап общественного развития, общественного движения. См. также Период в музыке, Период в… … Большая советская энциклопедия
ПЕРИОД — (от греческого periodos обход, круговращение, определенный круг времени), 1) промежуток времени, охватывающий какой либо законченный процесс. 2) Этап общественного развития, общественного движения … Современная энциклопедия
ПЕРИОД — (от греч. periodos обход круговращение, определенный круг времени), 1) промежуток времени, охватывающий какой либо законченный процесс.2) Этап общественного развития, общественного движения … Большой Энциклопедический словарь
ПЕРИОД ГРАФИКА — время занятия перегона парой поездов или группой чередующихся поездов, характерной для разных типов графика (парного, непарного, пачечного, пакетного). П. г. однопутной линии (фиг. 1) состоит из суммы времени занятия перегона в обоих направлениях … Технический железнодорожный словарь
Движение по окружности, период обращения и частота.
1. Равномерное движение по окружности
Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.
Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.
Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.
Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.
Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.
2. Период вращения и вращающаяся частота
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.
Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.
Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.
При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:
Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: 
Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:
частота вращения равна количеству полных оборотов за одну секунду.
Частота вращения и период обращения связаны следующим соотношением:
Частоту в СИ измеряют в
3. Вращательное движение
В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.
Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.
Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
ПРОВЕРЬТЕ СЕБЯ
1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.
2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: 
3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.