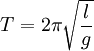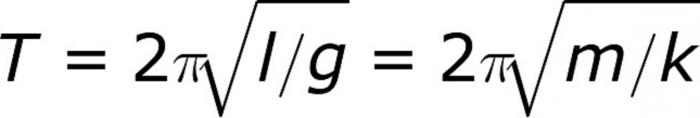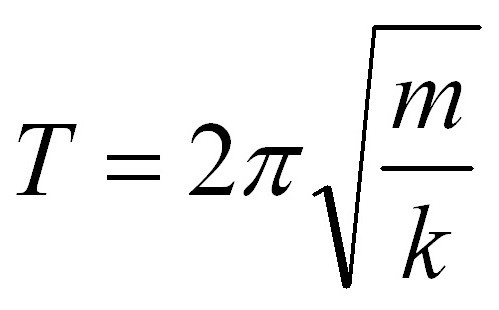Что такое период колебаний

Период колебания

Пери́од колеба́ний — наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно).

Содержание

Периоды простейших физических систем

Период колебаний математического маятника

Период колебаний математического маятника выражается по следующей формуле:

Период колебаний физического маятника

Период колебаний пружинного маятника

где m — масса груза, k — жесткость пружины.

Полезное

Смотреть что такое «Период колебания» в других словарях:

ПЕРИОД КОЛЕБАНИЯ — (period of oscillation) Отрезок времени, который требуется колебательной функции, для того чтобы вернуться в любую заданную точку своего цикла. Функции y=acosx или z=bsinx имеют период колебания, равный 2π; если цикл достигает заданной точки,… … Экономический словарь

период колебания — 1. Наименьший промежуток времени, за который совершается один цикл колебания. Для периодических колебаний время, за которое совершается одно полное колебание. 2. Время, за которое совершается один полный цикл колебания. Единица измерения с [BS EN … Справочник технического переводчика

период колебания — svyravimo periodas statusas T sritis fizika atitikmenys: angl. oscillation period vok. Schwingungsperiode, f rus. период колебания, m pranc. période d’oscillation, f … Fizikos terminų žodynas

период колебания — svyravimo laikotarpis statusas T sritis Kūno kultūra ir sportas apibrėžtis Svyruojamųjų judesių apibūdinimas – trumpiausias laiko tarpas, per kurį svyruojanti sistema grįžta į pradinę padėtį. Svyravimo laikotarpio dydis yra atvirkščias svyravimo… … Sporto terminų žodynas

основной период колебания здания в интересующем горизонтальном направлении — T1 — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы T1 EN fundamental period of the building in the horizontal direction of interest … Справочник технического переводчика

период колебаний — период Наименьший промежуток времени, через который повторяется состояние механической системы, характеризуемое значениями обобщенных координат и их производных. [Сборник рекомендуемых терминов. Выпуск 106. Механические колебания. Академия наук… … Справочник технического переводчика

период колебаний (вибрации) — период Наименьший интервал времени, через который при периодических колебаниях (вибрации) повторяется каждое значение колеблющейся величины (характеризующей вибрацию). Пояснения Термины и определения для близких понятий, различающиеся лишь… … Справочник технического переводчика

КОЛЕБАНИЯ — КОЛЕБАНИЯ, процессы (в наиболее общем смысле), периодически меняющие свое направление со временем. Процессы эти могут быть весьма разнообразными. Если напр. подвесить на стальной спиральной пружине тяжелый шар, оттянуть его и затем предоставить… … Большая медицинская энциклопедия

Источник

Период колебаний

Из Википедии — свободной энциклопедии

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота [3] колебаний его волновой функции).

Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Источник

Характеристики колебаний

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

\( \large T \left( c \right) \) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

\( \large \nu \left( \frac<1> \right) \).

Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1> = c^ <-1>\).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

\( \large \displaystyle \omega \left( \frac<\text<рад>> \right) \)

Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».

Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.

Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>\) и вычислить частоту \( \large \nu \).

И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).

\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.

Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]

Из графика следует, что период T = 4 сек.

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Для этого используем формулу:

\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)

Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».

Примечания:

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

\( \large \varphi_<01>\) – для первого процесса и,

\( \large \varphi_<02>\) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);

\( \large N \left( \text <шт>\right) \) – количество полных колебаний;

\( \large t \left( c \right) \) – общее время для нескольких колебаний;

\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.

\(\large \displaystyle \omega \left( \frac<\text<рад>> \right) \) – циклическая (круговая) частота колебаний.

\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;

\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;

\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Источник

Период колебаний: опыты, формулы, задачи

Что такое период колебаний? Что это за величина, какой физический смысл она имеет и как ее рассчитать? В этой статье мы разберемся с этими вопросами, рассмотрим различные формулы, по которым можно рассчитать период колебаний, а также выясним, какая связь имеется между такими физическими величинами, как период и частота колебаний тела/системы.

Определение и физический смысл

Периодом колебаний называется такой промежуток времени, при котором тело или система совершают одно колебание (обязательно полное). Параллельно можно отметить параметр, при выполнении которого колебание может считаться полным. В роли такого условия выступает возвращение тела в его первоначальное состояние (к первоначальной координате). Очень хорошо проводится аналогия с периодом функции. Ошибочно, кстати, думать, что она имеет место исключительно в обыкновенной и высшей математике. Как известно, эти две науки неразрывно связаны. И с периодом функций можно столкнуться не только при решении тригонометрических уравнений, но и в различных разделах физики, а именно речь идет о механике, оптике и прочих. При переносе периода колебаний из математики в физику под ним нужно понимать просто физическую величину (а не функцию), которая имеет прямую зависимость от проходящего времени.

Какие бывают колебания?

Колебания подразделяются на гармонические и ангармонические, а также на периодические и непериодические. Логично было бы предположить, что в случае гармонических колебаний они совершаются согласно некоторой гармонической функции. Это может быть как синус, так и косинус. При этом в деле могут оказаться и коэффициенты сжатия-растяжения и увеличения-уменьшения. Также колебания бывают затухающими. То есть, когда на систему действует определенная сила, которая постепенно “тормозит” сами колебания. При этом период становится меньше, в то время как частота колебаний неизменно увеличивается. Очень хорошо демонстрирует такую вот физическую аксиому простейший опыт с использованием маятника. Он может быть пружинного вида, а также математического. Это неважно. Кстати, период колебаний в таких системах будет определяться разными формулами. Но об этом чуточку позже. Сейчас же приведем примеры.

Опыт с маятниками

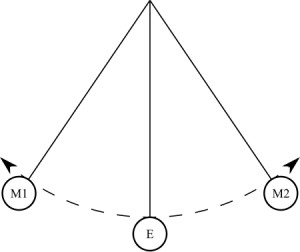
Взять первым можно любой маятник, разницы никакой не будет. Законы физики на то и законы физики, что они соблюдаются в любом случае. Но почему-то больше по душе математический маятник. Если кто-то не знает, что он собой представляет: это шарик на нерастяжимой нити, который крепится к горизонтальной планке, прикрепленной к ножкам (или элементам, которые играют их роль – держать систему в равновесном состоянии). Шарик лучше всего брать из металла, чтобы опыт был нагляднее.

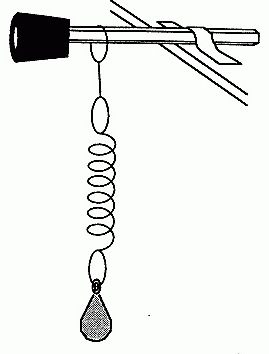
Итак, если вывести такую систему из равновесия, приложить к шару какую-то силу (проще говоря, толкнуть его), то шарик начнет раскачиваться на нити, следуя определенной траектории. Со временем можно заметить, что траектория, по которой проходит шар, сокращается. В то же время шарик начинает все быстрее сновать туда-сюда. Это говорит о том, что частота колебаний увеличивается. А вот время, за которое шарик возвращается в начальное положение, уменьшается. А ведь время одного полного колебания, как мы выяснили ранее, и называется периодом. Если одна величина уменьшается, а другая увеличивается, то говорят об обратной пропорциональности. Вот мы и добрались до первого момента, на основании которого строятся формулы для определения периода колебаний. Если же мы возьмем для проведения пружинный маятник, то там закон будет наблюдаться немного в другом виде. Для того чтобы он был наиболее наглядно представлен, приведем систему в движение в вертикальной плоскости. Чтобы было понятнее, сначала стоило сказать, что собой представляет пружинный маятник. Из названия понятно, что в его конструкции должна присутствовать пружина. И это действительно так. Опять же таки, у нас есть горизонтальная плоскость на опорах, к которой подвешивается пружина определенной длины и жесткости. К ней, в свою очередь, подвешивается грузик. Это может быть цилиндр, куб или другая фигурка. Это может быть даже какой-то сторонний предмет. В любом случае, при выведении системы из положения равновесия, она начнет совершать затухающие колебания. Наиболее четко просматривается увеличение частоты именно в вертикальной плоскости, без всякого отклонения. На этом с опытами можно закончить.

Итак, в их ходе мы выяснили, что период и частота колебаний это две физические величины, которые имеют обратную зависимость.

Обозначение величин и размерности

Обычно период колебаний обозначается латинской буквой T. Гораздо реже он может обозначаться по-другому. Частота же обозначается буквой µ (“Мю”). Как мы говорили в самом начале, период это не что иное, как время, за которое в системе происходит полное колебание. Тогда размерностью периода будет секунда. А так как период и частота обратно пропорциональны, то размерностью частоты будет единица, деленная на секунду. В записи задач все будет выглядеть таким образом: T (с), µ (1/с).

Формула для математического маятника. Задача №1

Как и в случае с опытами, я решил первым делом разобраться с маятником математическим. Подробно вдаваться в вывод формулы мы не будем, поскольку такая задача поставлена изначально не была. Да и вывод сам по себе громоздкий. Но вот с самими формулами ознакомимся, выясним, что за величины в них входят. Итак, формула периода колебаний для математического маятника имеет следующий вид:

Где l – длина нити, п = 3,14, а g – ускорение свободного падения (9,8 м/с^2). Никаких затруднений формула вызывать не должна. Поэтому без дополнительных вопросов перейдем сразу к решению задачи на определение периода колебания математического маятника. Металлический шар массой 10 грамм подвешен на нерастяжимой нити длиной 20 сантиметров. Рассчитайте период колебания системы, приняв ее за математический маятник. Решение очень простое. Как и во всех задачах по физике, необходимо максимально упростить ее за счет отброса ненужных слов. Они включаются в контекст для того чтобы запутать решающего, но на самом деле никакого веса абсолютно не имеют. В большинстве случаев, разумеется. Здесь можно исключить момент с “нерастяжимой нитью”. Это словосочетание не должно вводить в ступор. А так как маятник у нас математический, масса груза нас интересовать не должна. То есть слова о 10 граммах тоже просто призваны запутать ученика. Но мы ведь знаем, что в формуле масса отсутствует, поэтому со спокойной совестью можем приступать к решению. Итак, берем формулу и просто подставляем в нее величины, поскольку определить необходимо период системы. Поскольку дополнительных условий не было задано, округлять значения будем до 3-его знака после запятой, как и принято. Перемножив и поделив величины, получим, что период колебаний равен 0,886 секунд. Задача решена.

Формула для пружинного маятника. Задача №2

Формулы маятников имеют общую часть, а именно 2п. Эта величина присутствует сразу в двух формулах, но разнятся они подкоренным выражением. Если в задаче, касающейся периода пружинного маятника, указана масса груза, то избежать вычислений с ее применение невозможно, как это было в случае с математическим маятником. Но пугаться не стоит. Вот так выглядит формула периода для пружинного маятника:

В ней m – масса подвешенного к пружине груза, k – коэффициент жесткости пружины. В задаче значение коэффициента может быть приведено. Но если в формуле математического маятника особо не разгуляешься – все-таки 2 величины из 4 являются константами – то тут добавляется 3 параметр, который может изменяться. И на выходе мы имеем 3 переменных: период (частота) колебаний, коэффициент жесткости пружины, масса подвешенного груза. Задача может быть сориентирована на нахождение любого из этих параметров. Вновь искать период было бы слишком легко, поэтому мы немного изменим условие. Найдите коэффициент жесткости пружины, если время полного колебания составляет 4 секунды, а масса груза пружинного маятника равна 200 граммам.

Для решения любой физической задачи хорошо бы сначала сделать рисунок и написать формулы. Они здесь – половина дела. Записав формулу, необходимо выразить коэффициент жесткости. Он у нас находится под корнем, поэтому обе части уравнения возведем в квадрат. Чтобы избавиться от дроби, умножим части на k. Теперь оставим в левой части уравнения только коэффициент, то есть разделим части на T^2. В принципе, задачку можно было бы еще немного усложнить, задав не период в числах, а частоту. В любом случае, при подсчетах и округлениях (мы условились округлять до 3-его знака после запятой), получится, что k = 0, 157 Н/м.

Период свободных колебаний. Формула периода свободных колебаний

Под формулой периода свободных колебаний понимают те формулы, которые мы разобрали в двух ранее приведенных задачах. Составляют также уравнение свободных колебаний, но там речь идет уже о смещениях и координатах, а этот вопрос относится уже к другой статье.

Советы для решения задач, связанных с периодом

1) Прежде чем браться за задачу, запишите формулу, которая с ней связана.

2) Простейшие задачи не требуют рисунков, но в исключительных случаях их нужно будет сделать.

3) Старайтесь избавляться от корней и знаменателей, если это возможно. Записанное в строчку уравнение, не имеющее знаменателя, решать гораздо удобнее и проще.

Источник