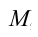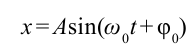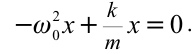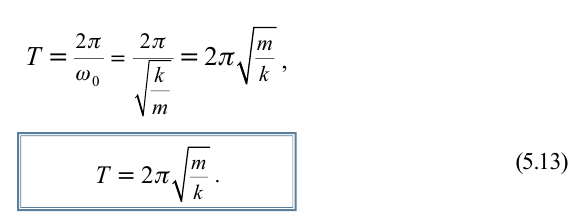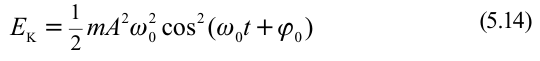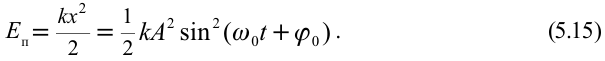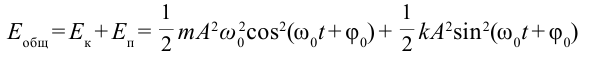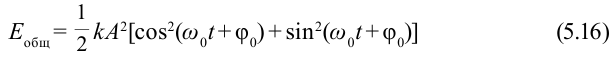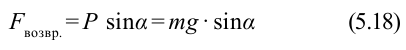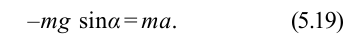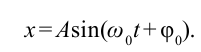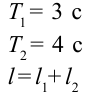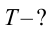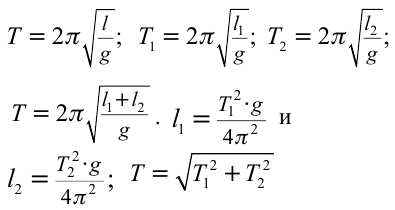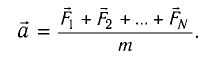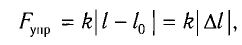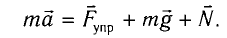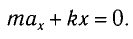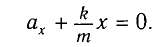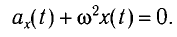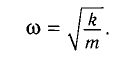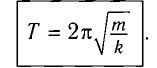Что такое период маятника

Содержание:

Пружинные и математические маятники:

Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.

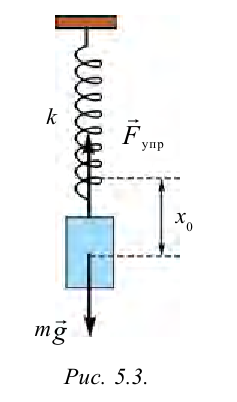
Система, состоящая из груза массой

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:

Если учесть, что ускорение тела, совершающего гармонические колебания 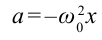, то уравнение (5.10) примет вид:

Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника.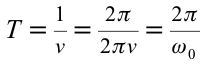

Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
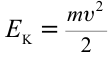
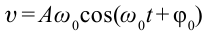
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, . В предыдущих темах было показано, что скорость можно выразить формулой . В таком случае кинетическая энергия маятника равна

Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:

В большинстве случаев важно знать полную энергию системы:

Если учесть, что ,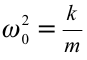

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
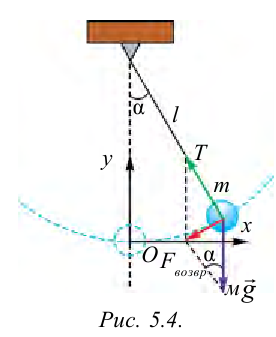
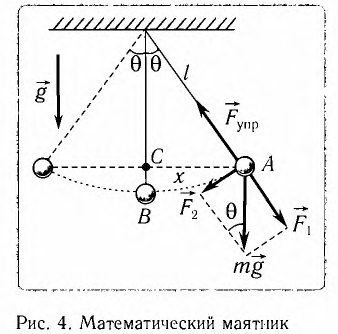
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.

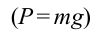
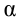
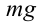
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки уравновешивает силу натяжения (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол , силы и не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.

Из рис. 5.4. видим, что:

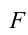
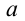
Согласно второму закону Ньютона, сила придает материальной точке ускорение , поэтому

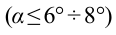
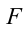
Из-за того, что угол наклона очень маленький , а сила направлена противоположно смещению, формулу (5.19) можно записать в виде

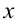
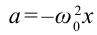
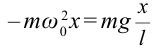
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой и учитывать соотношение , получим
Следовательно
Исходя из смысла периода колебания и учитывая, что 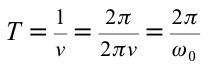получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:

Отсюда колебание математического маятника записывается следующим выражением:

Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 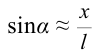и для решения уравнения движения не применяется закон синусов или косинусов.

Пример:

Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.

Решение: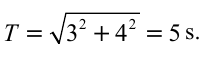

Ответ: 5 cек.

Пружинный и математический маятники

Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:

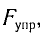
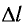
Закон Гука: модуль силы упругости , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) :

где k — жесткость тела, 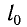— длина недеформированного тела, l — длина деформированного тела.

Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.

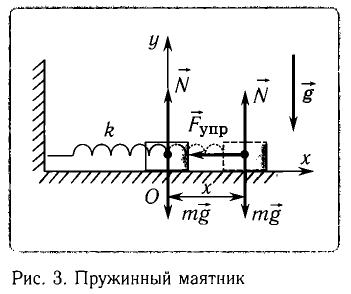
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).

Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 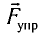направленная влево.

Запишем второй закон Ньютона для движения груза:

В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем

или

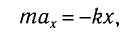
Это уравнение аналогично уравнению гармонических колебаний

Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:

Тогда период колебаний пружинного маятника можно найти по формуле

Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).

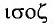
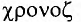
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов , — равный и — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.

Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.

Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).

Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.

Галилео Галилей экспериментально определил, что период малых колебаний (9

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Гармонические колебания

9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний

T = t/N

N — количество колебаний [-]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [-]

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

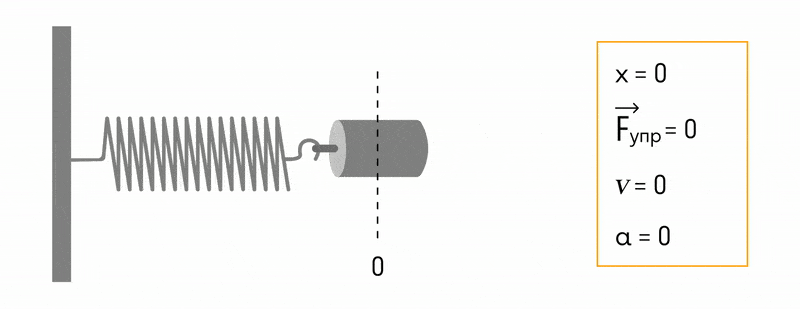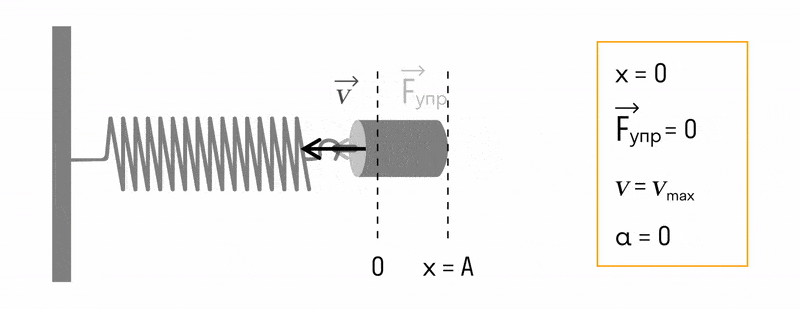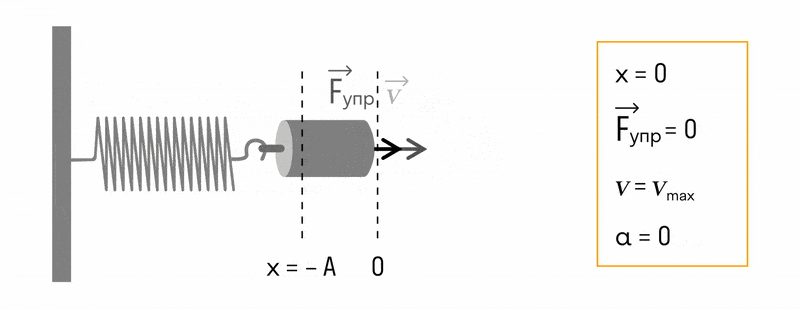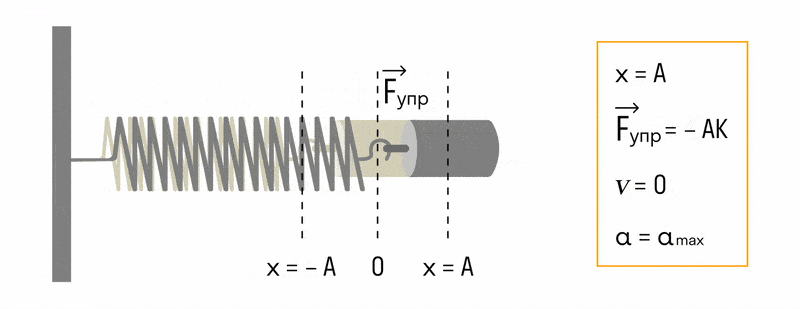
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

g — ускорение свободного падения [м/с^2]

На планете Земля g = 9,8 м/с2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Источник

Период колебаний математического маятника

Математический маятник — что это такое

Маятник — твердое тело, которое совершает под действием приложенных сил механические колебания около неподвижной точки или оси.

Простейший маятник состоит из небольшого груза массой m, подвешенного на невесомой нити или тонком стержне длиной l и совершающего колебания под воздействием земного притяжения. Если нить считать нерастяжимой, размер груза незначительным по сравнению с длиной нити, а массу нити незначительной по сравнению с массой груза, то груз можно считать материальной точкой массой m, находящейся на постоянном расстоянии l от точки подвеса. Такой маятник называют математическим.

Определение модели системы

Математические модели динамических систем часто используют для анализа самых разных технических, социально-экономических, естественнонаучных систем, в которых происходят циклические процессы.
Существуют различные классификации динамических процессов. Одна из них изображена на схеме:

Маятник Фуко

Отсюда следует, что если бы Земля не вращалась, данного эффекта просто не существовало бы. Это обстоятельство указывает на то, что причиной неинерциальности земной системы отсчета является вращение планеты.

Центробежное ускорение на экваторе равно 0,034 м/с^2. По сравнению с экваториальным ускорением свободного падения g = 9,78 м/с^2 это величина малая, но она заметно влияет на изменение веса тела на экваторе по сравнению с его весом на полюсе. Если, например, взвешивать на пружинных весах тело массой 10 кг, то уменьшение веса на экваторе за счет действия центробежной силы составит около 35 г.

Период колебаний математического маятника

Период колебаний — время, за которое происходит одно полное колебание. В СИ измеряется в секундах.

Чему равен, от чего зависит частота

Если за время t совершается N колебаний, то период, обозначаемый буквой T, равен

где v — частота колебаний. Она обратно пропорциональна периоду.
Колебания можно изобразить в виде графика:

Источник: physik.ucoz.ru.
Период колебаний математического маятника можно рассчитать по формуле

g — ускорение свободного падения. Не зависит от амплитуды колебаний и массы груза.

В случае математического маятника она определяется длиной подвеса и ускорением свободного падения:

Для физического маятника в уравнение добавляются инерция и масса подвеса:

Для пружинного маятника частоту определяет жесткость пружины k:

Уравнения движения и их решение, формулы с примерами

Математический маятник — это материальная точка, имеющая массу m и подвешенная на нити с неизменяемой длиной l. Покидая положение равновесия, подвес совершает колебательные движения по дуге.

Это дает нам дифференциальное уравнение гармонических колебаний

Из уравнения следует, что при малых углах отклонения от положения равновесия маятник будет колебаться с периодом

Из этого следует, что

Начальная фаза зависит от того, как маятник вывели из положения равновесия. Рассмотрим ситуацию, в которой маятник отклонили от положения равновесия на расстояние А и отпустили без начальной скорости. Запишем уравнение движения колеблющегося тела с учетом того факта, что в начальный момент координата тела будет равна А:

x = A × cos ω t + φ 0 ;

Уравнение движения маятника:

Если маятник толкнули, когда он находился в положении равновесия, начальная координата колеблющейся точки будет равна нулю:

Будет ли начальная координата положительной или отрицательной, определяет выбор положительного направления оси. Если направление оси совпадет с направлением начальной скорости, то в уравнении движения будет знак «плюс», если не совпадет — знак «минус».

Уравнение движения маятника:

Рассмотрим задачи, для которых требуется составлять и решать уравнения движения.

Необходимо определить амплитуду и частоту колебаний точки, если известно, что при смещении точки от положения равновесия на 5 см ее скорость равна 6 см/с, а при смещении на 3 см — 10 см/с.

Исключаем время из системы:

x 1 2 + v 1 2 ω 2 = А 2 x 2 2 + v 2 2 ω 2 = А 2

Преобразовав выражения и подставив значения, данные в условиях задачи, получаем:

Необходимо вычислить циклическую частоту колебаний точки, если известно, что при скорости 13 см/с ускорение равнялось 6 см/с^2, а при уменьшении скорости до 12 см/с произошло увеличение ускорения до 10 см/с^2.

Решение:
Координата точки меняется по закону

Запишем уравнения скорости и ускорения точки:

Преобразуем уравнение, исключив из него А, и подставим значения, данные в условиях задачи:

Практическое применение математического маятника

С помощью математического моделирования динамических систем можно обнаружить схожесть динамических процессов в реальных физических, технических, биологических, химических и социально-экономических системах. Разработка моделей, позволяющих предсказывать время и другие характеристики периодических процессов в этих системах, является эффективным способом анализировать, например, сельскохозяйственные или производственно-экономические процессы.

Источник