Что такое периодические сигналы
Периодический сигнал
Употребляется в документе:
Сигналы радиотехнические измерительные. Термины и определения
Смотреть что такое «Периодический сигнал» в других словарях:
периодический сигнал — Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени. x(t) = x(t iT), где i любое целое число [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины классификация измерительных… … Справочник технического переводчика
Периодический сигнал — 6. Периодический сигнал Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени x(t) = x(t iT), где i любое целое число Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и… … Словарь-справочник терминов нормативно-технической документации
периодический сигнал — periodinis signalas statusas T sritis automatika atitikmenys: angl. periodic wave vok. periodische Welle, f rus. периодический сигнал, m pranc. onde périodique, f … Automatikos terminų žodynas
сигнал — cигнал 1. Материальный носитель информации, содержащий в себе информацию, кодированную определенным образом. 2. Любая физическая величина (например, температура, давление воздуха, интенсивность света и т. п.), которая изменяется со временем.… … Справочник технического переводчика
гармонический сигнал — ; А амплитуда гармоничного сигнала; w круговая частота; j начальная фаза Примечание Периодический сигнал может быть образован путем периодического повторения импульсов. Соответствующие термины и определения для такого сигнала вводятся так же, как … Справочник технического переводчика
опорный сигнал — Периодический сигнал, с помощью которого осуществляется синхронизация всех основных элементов системы. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002]… … Справочник технического переводчика
ГОСТ 16465-70: Сигналы радиотехнические измерительные. Термины и определения — Терминология ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения оригинал документа: 40. Абсолютное отклонение сигналов Максимальное значение разности мгновенных значений сигналов, взятых в один и тот же момент времени на … Словарь-справочник терминов нормативно-технической документации
Меандр (радиотехника) — У этого термина существуют и другие значения, см. Меандр (значения). Меандр бесконечный, периодический сигнал прямоугольной формы, широко используемый в радиотехнике. Длительность импульса и длительность паузы в периоде такого сигнала равны … Википедия
Специальная теория относительности — Почтовая марка с формулой E = mc2, посвящённая Альберту Эйнштейну, одному из создателей СТО. Специальная теор … Википедия
Дискретное преобразование Фурье — (в англоязычной литературе DFT, Discrete Fourier Transform) это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а … Википедия
Связь между временной и частотной областями представления сигналов
Электрические сигналы можно исследовать во временной области с помощью осциллографа и в частотной области с помощью анализатора спектра (рисунок 1).
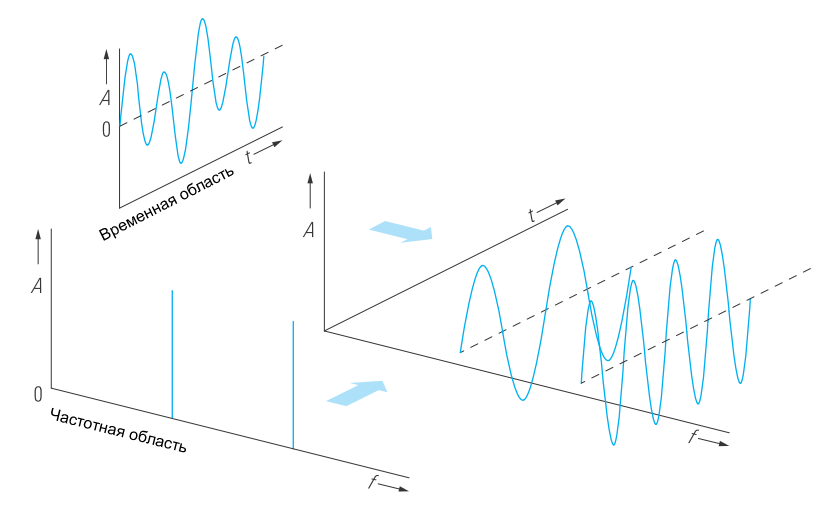
Эти два режима отображения сигналов связаны друг с другом преобразованием Фурье (обозначается как F), поэтому каждый сигнал во временной области имеет характерный частотный спектр. Таким образом, связь представлениями во временной и частотной областях будет следующей:
Чтобы проиллюстрировать эту взаимосвязь, сначала исследуем сигналы только с периодическим откликом во временной области.
Периодические сигналы
Согласно теореме Фурье любой сигнал, являющийся периодическим во временной области, может быть получен из суммы синусоидальных и косинусоидальных сигналов разной частоты и амплитуды. Такая сумма называется рядом Фурье. В этом случае применима следующая формула:
\[x(t) = \frac
Коэффициенты Фурье A0, An и Bn зависят от формы сигнала x(t) и могут быть рассчитаны следующим образом:
\[A_0 = \frac<2>
\[A_n = \frac<2>
\[B_n = \frac<2>
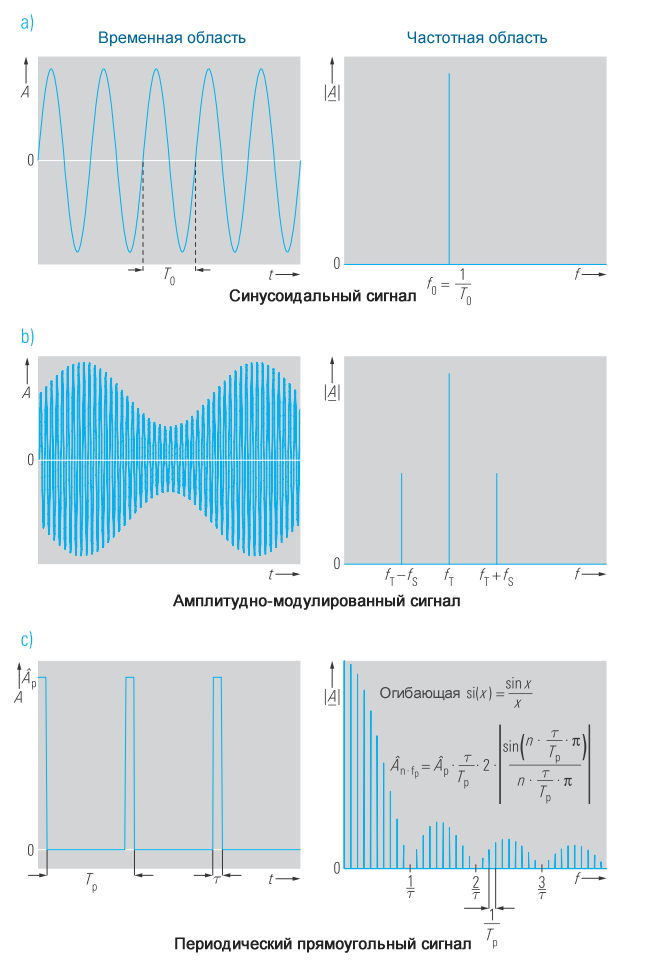
На рисунке 2b показан прямоугольный сигнал, аппроксимированный в ряд Фурье. Отдельные компоненты этого ряда Фурье показаны на рисунке 2a. Чем больше этих компонентов, тем итоговый сигнал ближе к идеальным прямоугольным импульсам.

В случае синусоидальных или косинусоидальных сигналов для уравнения 1 можно найти решение в замкнутой форме, и для отображения комплексного спектра будут получены следующие соотношения:
где \(\delta (f-f_0)\) – функция Дирака:
\[\begin
Можно видеть, что частотный спектр и синусоидального, и косинусоидального сигналов является функцией Дирака при f0 (смотрите рисунок 4a). Преобразования Фурье синусоидального и косинусоидального сигналов идентичны по величине, так что эти два сигнала демонстрируют идентичный амплитудный спектр на одной и той же частоте f0.
Чтобы вычислить частотный спектр периодического сигнала, временная характеристика которого описывается рядом Фурье в соответствии с уравнением 3, необходимо преобразовать каждый компонент ряда. Каждый из этих элементов приводит к функции Дирака, то есть дискретной составляющей в частотной области. Поэтому периодические сигналы всегда демонстрируют дискретные спектры, которые также называются линейчатыми спектрами. Например, спектр, показанный на рисунке 3, получен для аппроксимированного прямоугольного сигнала на рисунке 2.
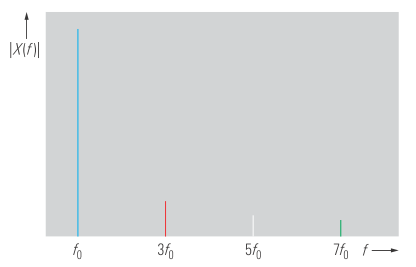
На рисунке 4 показаны еще несколько примеров периодических сигналов во временной и частотной областях.
Непериодические сигналы
Сигналы с непериодическим поведением во временной области не могут быть описаны рядом Фурье. Следовательно, частотный спектр таких сигналов не может быть составлен из дискретных спектральных составляющих. Непериодические сигналы демонстрируют непрерывный частотный спектр с частотно-зависимой спектральной плотностью. Представление такого сигнала в частотной области вычисляется с помощью преобразования Фурье (уравнение 1).
Подобно синусоидальным и косинусоидальным сигналам, решение уравнения 1 в замкнутой форме может быть найдено для многих сигналов. Таблицы с такими парами преобразований можно найти в [1].
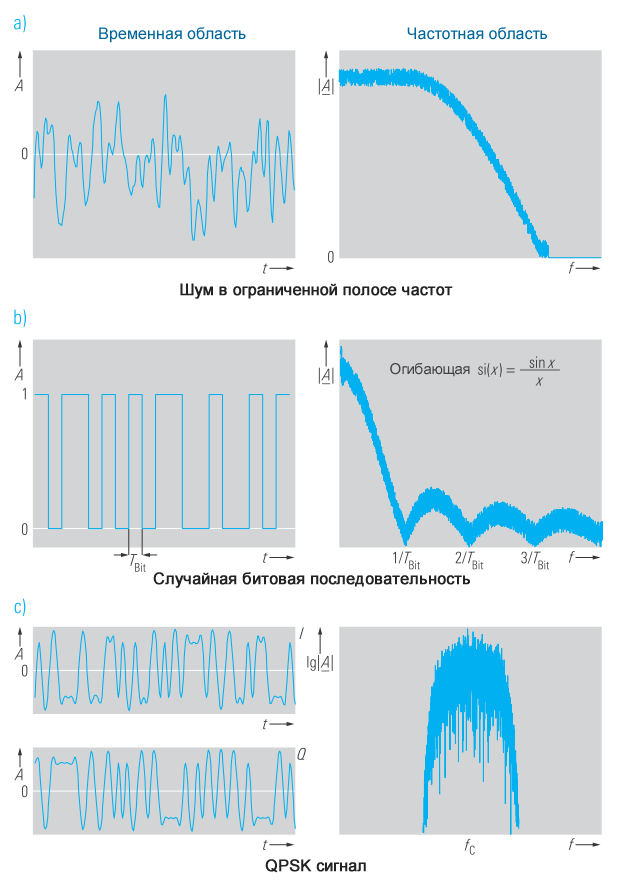
Для сигналов со случайными характеристиками во временной области, таких как шум или случайные битовые последовательности, решение в замкнутой форме встречается редко. В этом случае частотный спектр легче определить численным решением уравнения 1.
На рисунке 5 показаны некоторые непериодические сигналы во временной и частотной областях.
В зависимости от типа выполняемого измерения, полезными могут быть исследования либо во временной, либо в частотной области. Например, для измерения джиттера сигнала цифровой передачи данных требуется осциллограф. Для определения содержания гармоник более полезно исследовать сигнал в частотной области.
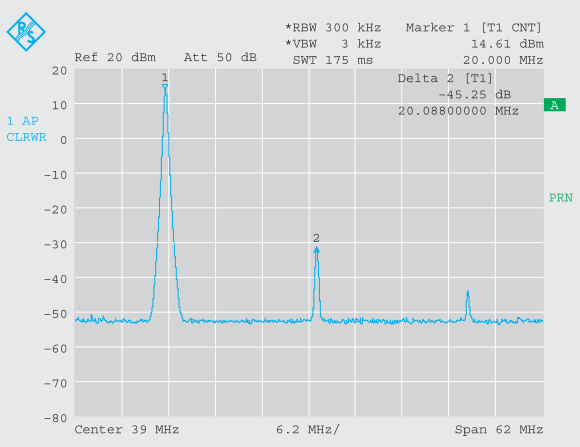
Сигнал, показанный на рисунке 6, кажется чистой синусоидой с частотой 20 МГц. Исходя из приведенных выше соображений, можно было бы ожидать, что его частотный спектр будет состоять только из одного компонента на частоте 20 МГц.
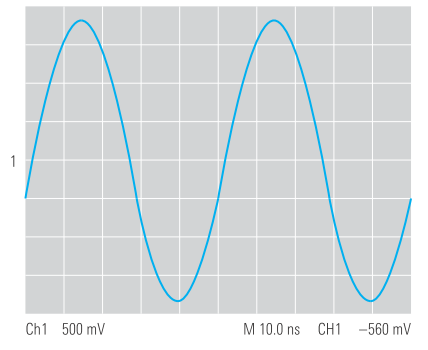
Однако при исследовании сигнала в частотной области с помощью анализатора спектра становится очевидным, что основная гармоника (гармоника 1-го порядка) накладывается на несколько гармоник более высокого порядка, то есть кратные 20 МГц (рисунок 7). Исследуя сигнал во временной области, эту информацию получить нелегко, и практическая количественная оценка высших гармоник невозможна. Кратковременную стабильность частоты и амплитуды синусоидального сигнала намного легче исследовать в частотной области, чем во временной (смотрите также раздел 6.1 «Измерение фазового шума).
Основы цифровой обработки сигналов
Сигнал это изменение физической величины во времени или пространстве. К примеру, это может быть изменение одномерного сигнала в зависимости от времени. Если мы рассматриваем цифровое изображение это может быть изменение яркости пикселей в зависимости от его положения в пространстве.
Но с точки зрения математики сигнал это функция одной или нескольких независимых переменных. В нашем случае независимыми переменными являются время и положение в пространстве, а зависимыми переменными могут быть значения нашего сигнала x от t или яркости пикселей на цифровом изображении.
Непрерывные и дискретные сигналы:
Непрерывный аналоговый сигнал определен на всем промежутке времени, то есть мы в любой момент времени t можем узнать значение сигнала x. Если мы возьмем эти значения с периодом дискретизации T, то мы получаем дискретный сигнал, значение которого определены только в конкретные моменты времени.
Дискретный сигнал теперь записываем как x[n], и n это номера отчетов дискретной последовательности. Если взглянуть на процесс дискретизации с точки зрения математики, то выходная дискретная последовательность с x[n] формируется, когда мы подставляем в нашу функцию x(t) значение времени t равный nT, где n — это номер дискретного отчета, а T — это период дискретизации.
Периодические сигналы
Периодический сигнал это сигнал, форма которого повторяется во времени. Повторяться во времени может, как форма непрерывных сигналов, так и форма дискретных сигналов. Периодом сигнала называем интервал повторения.
К примеру, у дискретного сигнала y[n] форма повторяется каждые 4, 8, 12 и так далее отчетов, для непрерывного сигнала z[t] форма повторяется каждые 2, 4, 6 и так далее секунд.
Фундаментальным или основным периодом сигналом называется наименьший интервал повторения, то есть для нашего дискретного сигнала y[n] это 4 отчета, а для нашего непрерывно сигнала это две секунды.
Фундаментальная частота
От понятие фундаментального периода мы можем перейти к понятию фундаментальной частоты. Фундаментальная или основная частота также именуемая первая гармоника, это количество основных периода сигнала, приходящихся на единицу времени. Частота измеряется в Герцах, то есть в количестве периодов приходящейся на одну секунду, и фактически является обратной величиной основного периода.
Если мы рассмотрим наш непрерывный сигнал z[t] его основной период равен двум секундам, а это значит, что на одну секунду приходится ровно половина его периода.
Основная частота дискретного сигнала
Но если с непрерывным сигналом все более менее понятно, то есть можем взглянуть на него на временной оси, оценить величины основного периода и подсчитать значение основной частоты, то с дискретным сигналом все не так просто.
Нам доступны значение отчетов, мы знаем их номера в последовательности, но мы не знаем, как они соотносятся с его фундаментальной частотой, и как они соотносятся с частотой дискретизации. Давайте в этом попробуем разобраться на примере.
Возьмем дискретный сигнал, который мы используем для описания в предыдущих статьях. Он имеет период в 4 отчета, где два первых отчета в периоде имеют большую амплитуду, а два последних отчета имеют малую амплитуду.
Нашей задачи в данном примере будет при помощи такого сигнала услышать ноту ля первой октавы, то есть частоту 440 Гц. Для того чтобы это сделать нам обязательно надо понять, как основная частота соотносится с частотой дискретизации сигнала.
Для этого давайте перенесем наш сигнал на временную ось. Основной период данного сигнала высчитывается также, как для непрерывного сигнала, то есть это обратная величина его фундаментальной частоты, в нашем случае единицы делить на 440. Но мы также видим то, что период дискретизации нашего сигнала, обозначим здесь его как ∆t в 4 раза меньше, чем основной период, так как на основной период приходится ровно 4 отсчета.
Выразим частоту дискретизации через период дискретизации, частоту дискретизации можно записать, как единицу делить на ∆t, что получить равно 4 делить на T0, то есть в нашем случае частота дискретизации должна быть в 4 раза больше, чем наша фундаментальная частота ноты ля первой октавы.
Изменение частоты дискретизации
Если мы рассмотрим наши манипуляции над дискретным сигналом, как манипуляции на аналоговом сигнале, а после этого дискретизацию аналогового сигнала, то вот к чему мы приходим. Когда мы увеличиваем частоту дискретизации, то мы фактически берем дискретные отчеты более быстрого аналогового сигнала, или кладем отчеты того же дискретного сигнала на другую временную сетку.
К примеру, наш дискретный сигнал с периодом дискретизации ∆t можно представить как оцифрованные значения аналогового сигнала с периодом Т0,
Если теперь те же самые отчеты сигнала, мы положим на более плотную временную сетку с меньшим периодом ∆t, это фактически то же самое как если мы оцифровали более быстрый аналоговый сигнал с меньшим периодом Т0.
В качестве эталонного, аналогового сигнала мы представили синусоиду, а почему мы так часто используем синусоиду, когда говорим о цифровой обработки сигналов об этом в следующей статье.
Что такое периодические сигналы
Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.
Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.
С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени. То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени. Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.
Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:
Периодические сигналы
Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц.
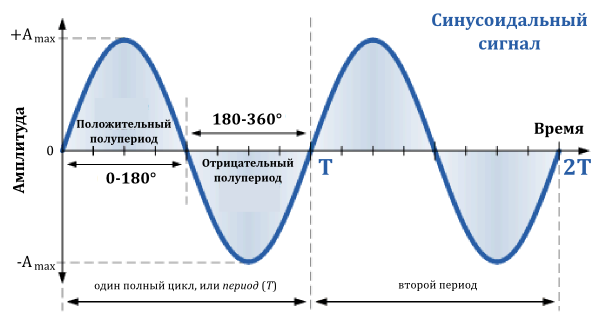
Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.
Период может изменяться от долей секунды до тысяч секунд, так как он связан с его частотой. Например, синусоидальный сигнал, которому требуется 1 секунда для совершения полного цикла, имеет период равный одной секунде. Аналогично, для синусоидального сигнала, которому требуется 5 секунд для совершения полного цикла, имеет период равный 5 секундам, и так далее.
Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов T в секунду, как показано на рисунке ниже.
Синусоидальный сигнал
Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).
Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360° (Т = 360°), или, если в радианах, то(T =
Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.
Соотношения между периодом сигнала и его частотой:
Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц, МГц, ГГц и даже ТГц
| Префикс | Определение | Запись | Период |
| Кило | тысяча | кГц | 1 мс |
| Мега | миллион | МГц | 1 мкс |
| Гига | миллиард | ГГц | 1 нс |
| Тера | триллион | ТГц | 1 пс |
Меандр
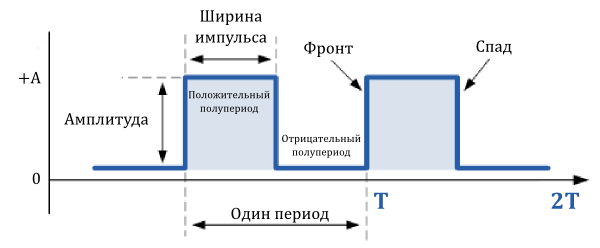
Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.
Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения периода.
Для меандра, время заполнения
равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:
Например, для сигнала с временем заполнения равным 10 мс, его частота равна:
Меандры используются в цифровых системах для представления уровня логической «1» большими значениями его амплитуды и уровня логического «0» маленькими значениями амплитуды.
Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным сигналом. В случае, или если время положительной части периода сигнала мало, то такой сигнал, является импульсом.
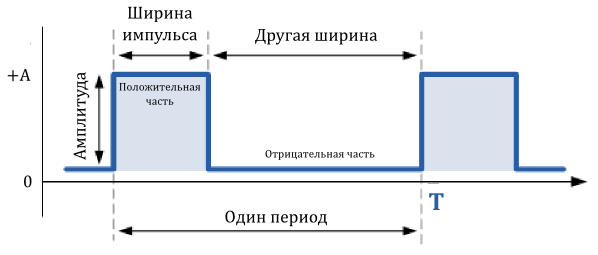
Прямоугольный сигнал
Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные сигналы.
В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.
На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.
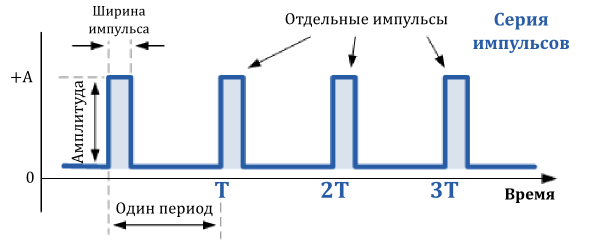
Отношение периода повторения сигнала, к длительности положительного импульса
Величину обратную скважности называют коэффициентом заполнения (duty cycle):
Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%. Необходимо найти частоту этого сигнала.
Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).
Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала. Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку. Отличным примером этого является использование широтно-импульсной модуляции в регуляторах скорости. Термин широтно-импульсная модуляция (ШИМ) буквально и означает «изменение ширины импульса».
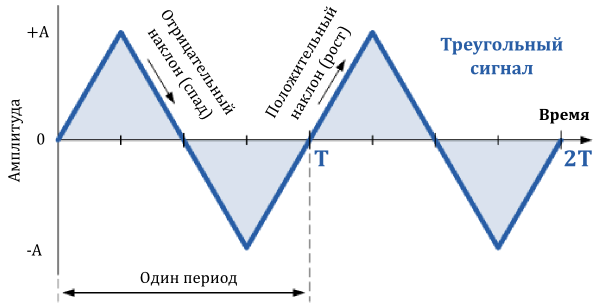
Треугольные сигналы
Треугольные сигналы, как правило, это двунаправленные несинусоидальные сигналы, которые колеблются между положительным и отрицательным пиковыми значениями. Треугольный сигнал представляет собой относительно медленно линейно растущее и падающее напряжение с постоянной частотой. Скорость, с которой напряжение изменяет свое направление равна для обоих половинок периода, как показано ниже.
Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.
В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал.
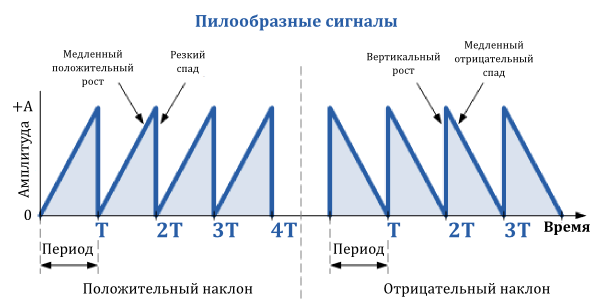
Пилообразный сигнал
Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.
Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным. Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f) и четных гармоник. Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.
Импульсы и запускающие сигналы (триггеры)
Хотя, технически, запускающие сигналы и импульсы два отдельных типа сигналов, но отличия между ними незначительны. Запускающий сигнал — это всего лишь очень узкий импульс. Разница в том, что триггер может быть как положительной, так и отрицательной полярности, тогда как импульс только положительным.
Форма импульса, или серии импульсов, как их чаще называют, является одним из видов несинусоидальной формы сигналов, похожей на прямоугольный сигнал. Разница в том, что импульсный сигнал определяется часто только коэффициентом заполнения. Для запускающего сигнала положительная часть сигнала очень короткая с резкими ростом и спадом и ее длительностью, по сравнению с периодом, можно пренебречь.
Очень короткие импульсы и запускающие сигналы предназначены для управления моментами времени, в которые происходят, например, запуск таймера, счетчика, переключение логических триггеров а также для управления тиристорами, симисторами и другими силовыми полупроводниковыми приборами.
Подробно я вернусь к ним в своих последующих публикациях.