Что такое перпендикуляр к плоскости

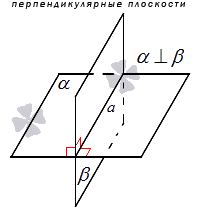
Перпендикулярные плоскости, условие перпендикулярности плоскостей

Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.

Перпендикулярные плоскости – основные сведения

При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.

При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.

Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.

Перпендикулярность плоскостей – признак и условие перпендикулярности

На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.

Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.

Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.

Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.

Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.

Рассмотрим подробнее на примерах.

Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.

Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.

Ответ: плоскости не перпендикулярны.

Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.

Ответ: плоскости перпендикулярны.

Источник

Что такое перпендикуляр к плоскости

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Перпендикуляр к плоскости. Наклонная

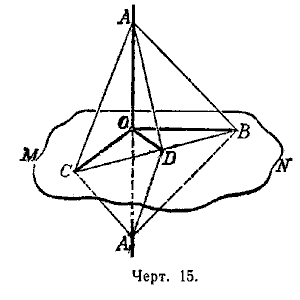
Поставим задачу определить, в каком случае прямая может считаться перпендикулярной к плоскости. Докажем предварительно следующее предложение.

Теорема. Если прямая (АА₁, черт. 15), пересекающаяся с плоскостью (МN), перпендикулярна к каким-нибудь двум прямым (ОВ и ОС), проведенным на этой плоскости через точку пересечения (O) данной прямой и плоскости, то она перпендикулярна и ко всякой третьей прямой (ОD), проведённой на плоскости через ту же точку пересечения (О).

Отложим на прямой АА₁ произвольной длины, но равные отрезки ОА и ОА₁ и проведём на плоскости какую-нибудь прямую, которая пересекала бы три прямые, исходящие из точки О, в каких-нибудь точках С, D и В. Эти точки соединим с точками А и А₁. Мы получим тогда несколько треугольников. Рассмотрим их в такой последовательности.

Сначала возьмём треугольники АСВ и А₁СВ; они равны, так как у них СВ—общая сторона, АС=А₁С, как наклонные к прямой АА₁, одинаково удалённые от основания О перпендикуляра ОС; по той же причине АВ = А₁В. Из равенства этих треугольников следует, что ∠ АВС = ∠ А₁BС.

После этого перейдём к треугольникам АОВ и А₁ОВ; они равны, так как у них ОВ—общая сторона, АВ = А₁В и ∠АВD = ∠А₁ВD. Из равенства этих треугольников выводим, что АО = А₁О.

Определение. Прямая называется перпендикулярной к плоскости, если она, пересекаясь с этой плоскостью, образует прямой угол с каждой прямой, проведённой на плоскости через точку пересечения. В этом случае говорят также, что плоскость перпендикулярна к прямой.

Из предыдущей теоремы следует, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум прямым, лежащим в данной плоскости и проходящим через точку пересечении данной прямой и плоскости.

Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к этой плоскости. Точка пересечения прямой с плоскостью называется основанием перпендикуляра или наклонной.

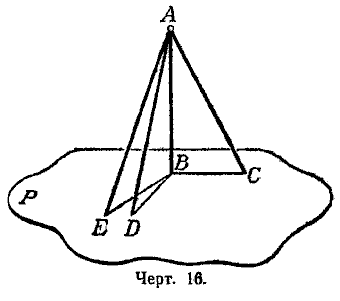
Сравнительная длина перпендикуляра и наклонных. Когда из одной точки А (черт. 16) проведены к плоскости перпендикуляр АВ и наклонная АС, условимся называть, проекцией наклонной на плоскость Р отрезок ВС, соединяющий основание перпендикуляра и основание наклонной.

Для краткости термины «перпендикуляр» и «наклонная» употребляются вместо «отрезок перпендикуляра, ограниченный данной точкой и основанием перпендикуляра», и «отрезок наклонной, ограниченный данной точкой и основанием наклонной.

Таким образом, отрезок ВС есть проекция наклонной АС, отрезок ВD есть проекция наклонной АD и т. д.

1) две наклонные, имеющие равные проекции, равны;

2) из двух наклонных та больше, проекция которой больше,

Вращая прямоугольные треугольники ABC и ABD вокруг катета AB, мы можем совместить их плоскости с плоскостью \(\Delta\)ABE. Тогда все наклонные будут лежать в одной плоскости с перпендикуляром, а все проекции расположатся на одной прямой. Таким образом, доказываемые теоремы приводятся к аналогичным теоремам планиметрии.

Обратные теоремы. Если из одной и той же точки, взятой вне плоскости, проведены перпендикуляр и какие-нибудь наклонные, то:

1) равные наклонные имеют равные проекции;

2) из двух проекций та больше, которая соответствует большей наклонной.

Приведём ещё следующую теорему о перпендикулярах, которая понадобится нам впоследствии.

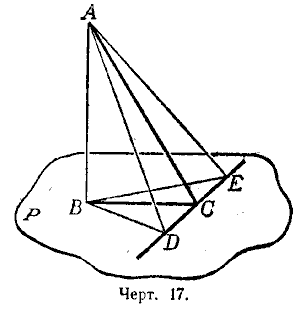
Теорема. Прямая (DЕ, черт. 17), проведённая на плоскости (Р) через основание наклонной (АС) перпендикулярно к её проекции (ВС), перпендикулярна и к самой наклонной.

Отложим произвольные, но равные отрезки СD и СЕ и соединим прямолинейными отрезками точки А и В с точками D и E. Тогда будем иметь:

ВD = ВЕ, как наклонные к прямой DЕ, одинаково удалённые от основания С перпендикуляра ВС;

АD = АЕ, как наклонные к плоскости Р, имеющие равные проекции ВD и ВЕ.

Вследствие этого \(\Delta\)АDЕ равнобедренный, и потому его медиана АС перпендикулярна к основанию DЕ.

Эта теорема носит название теоремы о трёх перпендикулярах. Действительно, в ней говорится о связи, соединяющей следующие три перпендикуляра:

1) АВ к плоскости Р,

2) ВС к прямой DE и

3) АС к той же прямой DE.

Обратная теорема. Прямая (ОЕ, черт. 17), проведённая на плоскости (Р) через основание наклонной (АС) перпендикулярно к этой наклонной, перпендикулярна и к её проекции.

Сделаем те же построения, что и при доказательстве прямой теоремы. Отложим произвольные, но равные отрезки СD и СЕ и соединим прямолинейными отрезками точки А и В с точками D и Е, тогда будем иметь:

АD = АЕ, как наклонные к прямой DЕ, одинаково удалённые от основания С перпендикуляра АС;

ВD = ВЕ, как проекции равных наклонных АD и АЕ.

Вследствие этого \(\Delta\)ВDЕ равнобедренный, и потому его медиана ВС перпендикулярна к основанию DЕ.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №10. Перпендикуляр и наклонные

Перечень вопросов, рассматриваемых в теме.

Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Обратная теорема: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Определение: углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения

Рассмотрим плоскость α и точку А, не лежащую в этой плоскости (рис. 1). Проведем через точку А прямую, перпендикулярную к плоскости α, и обозначим буквой Н точку пересечения этой прямой с плоскостью α. Отрезок АН называется перпендикуляром, проведенным из точки А к плоскости α, а точка Н — основанием перпендикуляра. Отметим в плоскости α какую-нибудь точку М, отличную от Н, и проведем отрезок AM. Он называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок НМ называется проекцией наклонной на плоскость α.

Источник

Перпендикуляр и наклонная. Расстояние от прямой до плоскости

Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

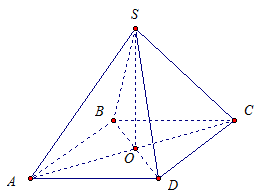
Пер­вый спо­соб.

Имеем квад­рат, центр квад­ра­та точка – О, SО – пер­пен­ди­ку­ляр. Зна­чит, для на­клон­ной SC от­ре­зок ОС есть про­ек­ция.

Пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой ОС, ко­то­рая яв­ля­ет­ся про­ек­ци­ей на­клон­ной SC, зна­чит, по тео­ре­ме о трех пер­пен­ди­ку­ля­рах, пря­мая ВD пер­пен­ди­ку­ляр­на на­клон­ной SC.

Вто­рой спо­соб.

Пря­мая SО пер­пен­ди­ку­ляр­на плос­ко­сти АВС, а зна­чит – и пря­мой ВD, ле­жа­щей в ней.

Пря­мая ВD пер­пен­ди­ку­ляр­на SО и пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой АС по свой­ству квад­ра­та.

По­лу­ча­ем, что пря­мая ВD пер­пен­ди­ку­ляр­на двум пе­ре­се­ка­ю­щим­ся пря­мым плос­ко­сти SОС, зна­чит, она пер­пен­ди­ку­ляр­на ко всей плос­ко­сти SОС, а зна­чит – и к пря­мой SC, ле­жа­щей в этой плос­ко­сти.

Расстояние от точки до плоскости есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ.

В единичном тетраэдре DABC найдите расстояние от точки C до плоскости ADB.

Основанием прямого параллелепипеда служит параллелограмм с углом 120 \(^\circ\) и сторонами, равными 3 и 4. Меньшая диагональ параллелепипеда равна большей диагонали основания. Найдите объем параллелепипеда.

Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.

Через вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная его плоскости. Расстояния от точки К до других вершин прямоугольника равны 12 м, 14 м, 18 м. Найдите отрезок АК.

Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС.

АВ = АС = 10 см, ВС = 12 см, AD = 6 см.

Найдите расстояние от точки D до ВС.

Через вершину прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскости прямоугольника.

Источник