Что такое перпендикуляр в геометрии 7 класс

Что такое перпендикуляр в геометрии 7 класс

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

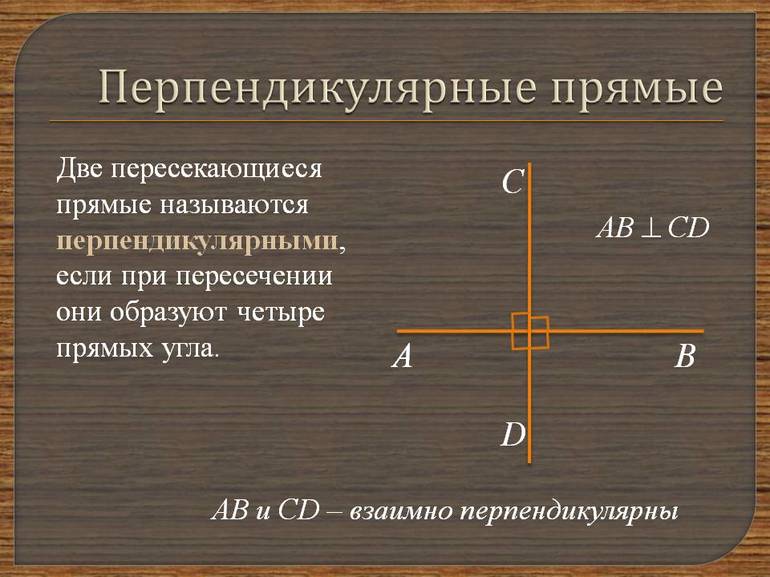
Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Геометрия. 7 класс

Конспект урока

Перпендикуляр к прямой

Перечень рассматриваемых вопросов:

Теорема – утверждение, справедливость которого устанавливается путём рассуждений.

Отрезок – часть прямой, ограниченная двумя точками.

Перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Теоретический материал для самостоятельного изучения.

Пешеходный переход, так называемая «зебра», расположен под углом 90 градусов к улице. Выбор такого угла сделан не случайно. Ведь перейти дорогу пешеходам необходимо как можно быстрее. Такой путь оказывается самым коротким. Чтобы быстрее добраться от метро Площадь Восстания в Санкт-Петербурге до Набережной реки Фонтанки, необходимо идти по Невскому проспекту, перпендикулярно реке.

Ножки стола крепятся перпендикулярно столешнице. Маятник часов расположен перпендикулярно верхней стенке часов.

Если считать улицу, набережную реки Фонтанки, ребро столешницы, ребро стенки часов моделями прямых, то можно говорить, что на каждой картинке построены перпендикуляры к прямой.

Примеры с картой и пешеходным переходом иллюстрируют тот факт, что перпендикуляр к прямой – это кратчайший путь от точки до прямой. Такой путь называется расстоянием.

Пример с часами поможет нам запомнить происхождение слова перпендикуляр. В переводе с французского перпендикуляр означает висеть. То есть, перпендикуляр – это отвес.

Дадим определение перпендикуляра к прямой.

Мы знаем, что перпендикулярными прямыми называются две пересекающиеся прямые, которые образуют при пересечении четыре прямых угла.

Часть одной из этих прямых является перпендикуляром к прямой.

Выделенная часть прямой ограничена двумя точками, значит, по определению, – это отрезок. Один из концов этого отрезка является точкой пересечения перпендикуляра и прямой, к которой он проведен.

перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Н – основание перпендикуляра.

Предположим, что вы купаетесь в море недалеко от берега. Вдруг появилась акула, необходимо срочно плыть к берегу. Конечно, вы выберите самый короткий путь. А мы уже знаем, что в геометрии этот путь называют перпендикуляром к прямой.

Всегда ли можно найти кратчайший путь? Сколько существует способов построения кратчайшего пути?

Если на пути нет препятствий, например, здания, ямы, в данном примере – других пловцов, то самый короткий путь проделать можно. И такой путь единственный.

В геометрии любое утверждение требует доказательства. Сформулируем теорему о перпендикуляре к прямой.

Теорема: из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

По условию теоремы нам даны прямая и точка.

Заключение теоремы состоит из двух частей – существование перпендикуляра и его единственность.

1.Через точку А можно провести перпендикуляр к прямой BC.

2.Данный перпендикуляр единственный.

Разбор заданий тренировочного модуля.

Задание 1. Построить перпендикуляр к прямой.

Для этого можно использовать чертёжный угольник, одну сторону которого от угла в 90 градусов прикладываем к прямой, к которой проведём перпендикуляр из точки, не лежащей на этой прямой, а вторую сторону угольника совместим с точкой, от которой проведём перпендикуляр к прямой.

Задание 2. На рисунке изображены два перпендикуляра АB и СD к прямой а, при этом АB = СD.

Докажем, что треугольники ABD и CDВ равны.

По условию в треугольниках ABD и CDВ, сторона АBравна стороне СD.

AB ⊥ а =>∠ABD = 90° (по определению перпендикулярных прямых).

СD ⊥ а => ∠CDВ = 90° (по определению перпендикулярных прямых).

Следовательно, ∠ABD = ∠CDВ.

Следовательно, ∆ABD = ∆CDВ

(по первому признаку равенства треугольников: по двум сторонам и углу между ними).

Источник

Геометрия. 7 класс

Конспект урока

Перпендикуляр к прямой

Перечень рассматриваемых вопросов:

Теорема – утверждение, справедливость которого устанавливается путём рассуждений.

Отрезок – часть прямой, ограниченная двумя точками.

Перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Теоретический материал для самостоятельного изучения.

Пешеходный переход, так называемая «зебра», расположен под углом 90 градусов к улице. Выбор такого угла сделан не случайно. Ведь перейти дорогу пешеходам необходимо как можно быстрее. Такой путь оказывается самым коротким. Чтобы быстрее добраться от метро Площадь Восстания в Санкт-Петербурге до Набережной реки Фонтанки, необходимо идти по Невскому проспекту, перпендикулярно реке.

Ножки стола крепятся перпендикулярно столешнице. Маятник часов расположен перпендикулярно верхней стенке часов.

Если считать улицу, набережную реки Фонтанки, ребро столешницы, ребро стенки часов моделями прямых, то можно говорить, что на каждой картинке построены перпендикуляры к прямой.

Примеры с картой и пешеходным переходом иллюстрируют тот факт, что перпендикуляр к прямой – это кратчайший путь от точки до прямой. Такой путь называется расстоянием.

Пример с часами поможет нам запомнить происхождение слова перпендикуляр. В переводе с французского перпендикуляр означает висеть. То есть, перпендикуляр – это отвес.

Дадим определение перпендикуляра к прямой.

Мы знаем, что перпендикулярными прямыми называются две пересекающиеся прямые, которые образуют при пересечении четыре прямых угла.

Часть одной из этих прямых является перпендикуляром к прямой.

Выделенная часть прямой ограничена двумя точками, значит, по определению, – это отрезок. Один из концов этого отрезка является точкой пересечения перпендикуляра и прямой, к которой он проведен.

перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Н – основание перпендикуляра.

Предположим, что вы купаетесь в море недалеко от берега. Вдруг появилась акула, необходимо срочно плыть к берегу. Конечно, вы выберите самый короткий путь. А мы уже знаем, что в геометрии этот путь называют перпендикуляром к прямой.

Всегда ли можно найти кратчайший путь? Сколько существует способов построения кратчайшего пути?

Если на пути нет препятствий, например, здания, ямы, в данном примере – других пловцов, то самый короткий путь проделать можно. И такой путь единственный.

В геометрии любое утверждение требует доказательства. Сформулируем теорему о перпендикуляре к прямой.

Теорема: из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

По условию теоремы нам даны прямая и точка.

Заключение теоремы состоит из двух частей – существование перпендикуляра и его единственность.

1.Через точку А можно провести перпендикуляр к прямой BC.

2.Данный перпендикуляр единственный.

Разбор заданий тренировочного модуля.

Задание 1. Построить перпендикуляр к прямой.

Для этого можно использовать чертёжный угольник, одну сторону которого от угла в 90 градусов прикладываем к прямой, к которой проведём перпендикуляр из точки, не лежащей на этой прямой, а вторую сторону угольника совместим с точкой, от которой проведём перпендикуляр к прямой.

Задание 2. На рисунке изображены два перпендикуляра АB и СD к прямой а, при этом АB = СD.

Докажем, что треугольники ABD и CDВ равны.

По условию в треугольниках ABD и CDВ, сторона АBравна стороне СD.

AB ⊥ а =>∠ABD = 90° (по определению перпендикулярных прямых).

СD ⊥ а => ∠CDВ = 90° (по определению перпендикулярных прямых).

Следовательно, ∠ABD = ∠CDВ.

Следовательно, ∆ABD = ∆CDВ

(по первому признаку равенства треугольников: по двум сторонам и углу между ними).

Источник

Перпендикуляр к прямой

Урок 7. Геометрия 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Перпендикуляр к прямой»

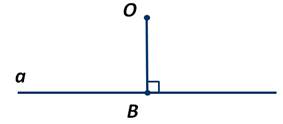
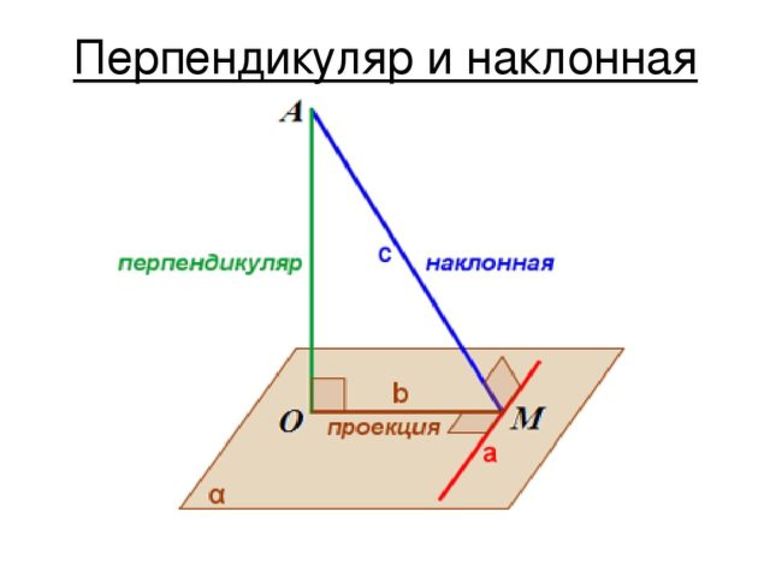
Рассмотрим понятие перпендикуляра к прямой. Возьмём прямую а и некоторую точку О, которая не лежит на этой прямой. Соединим точку О с точкой В, которая лежит на прямой а.

Отрезок ОВ называется перпендикуляром, проведённым из точки В к прямой а, если отрезок ОВ и прямая а перпендикулярны. Точку В называют основанием перпендикуляра.

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

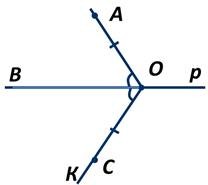
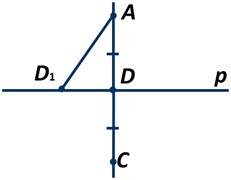
1. Существование перпендикуляра.

Пусть точка А не лежит на прямой p. Возьмём на этой прямой точку О и проведём луч ОA. Затем от луча ОB отложим угол BОK, равный углу АОВ. На луче ОK отложим отрезок ОС, равный отрезку ОA.

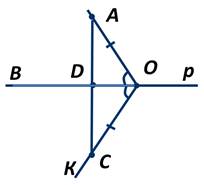
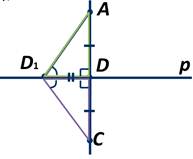
2. Единственность перпендикуляра.

Треугольник ADD₁ равен треугольнику СDD₁ по первому признаку, так как сторона DD₁ у них общая, сторона АD=СD, ∠ADD₁=∠СDD₁. Следовательно, ∠AD₁D=∠СD₁D.

Так как по предположению ∠AD₁D=90 градусов, то и ∠СD₁D=90 градусов, то есть ∠АD₁С развёрнутый и лучи D₁А и D₁С составляют прямую. Таким образом, получили, что через две точки А и С проходят две прямые, а ранее мы говорили, что это невозможно. Следовательно наше предположение неверно, то есть из точки А к прямой р можно провести только один перпендикуляр. Теорема доказана.

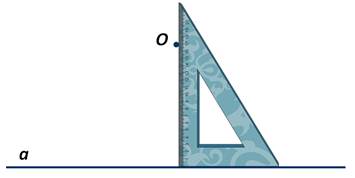
Чтобы провести перпендикуляр из точки О к прямой а используют чертёжный угольник.

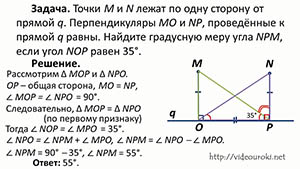
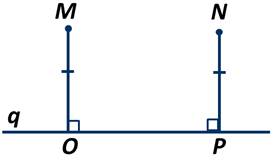
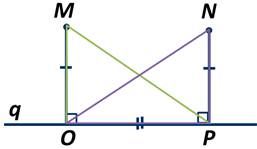
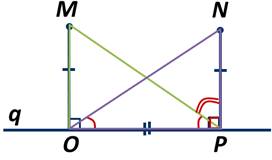
Точки M и N лежат по одну сторону от прямой q. Перпендикуляры МО и NP, проведённые к прямой q равны. Найти градусную меру ∠NPM, если ∠NOP=35 градусов.

∠NPO=∠NPM+∠MPO. Из этого равенства получаем, что ∠NPM=∠NPO-∠MPO.

Источник

Основные свойства

При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:

Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.

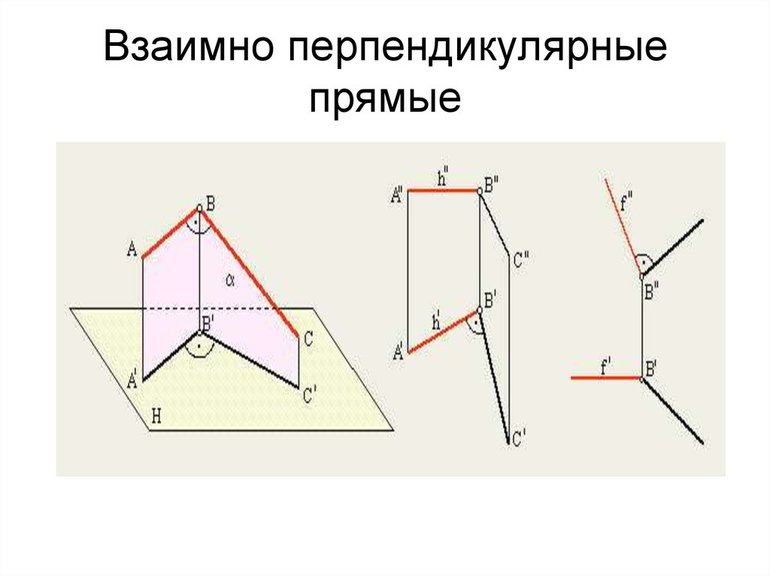
Доказательство взаимного расположения

Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:

Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.

Определение перпендикулярности прямой и плоскости

Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.

Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.

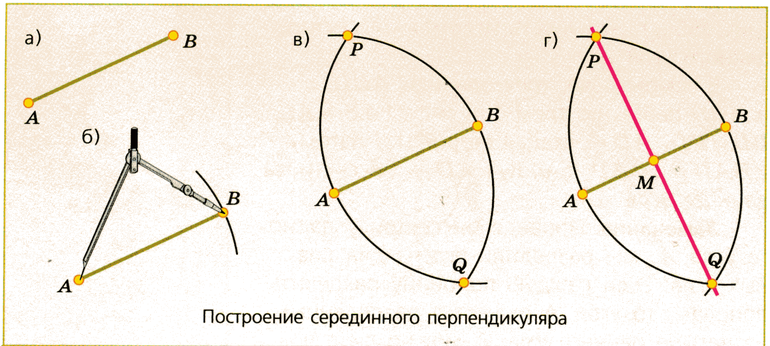
Построение перпендикуляра

Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:

Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:

В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.

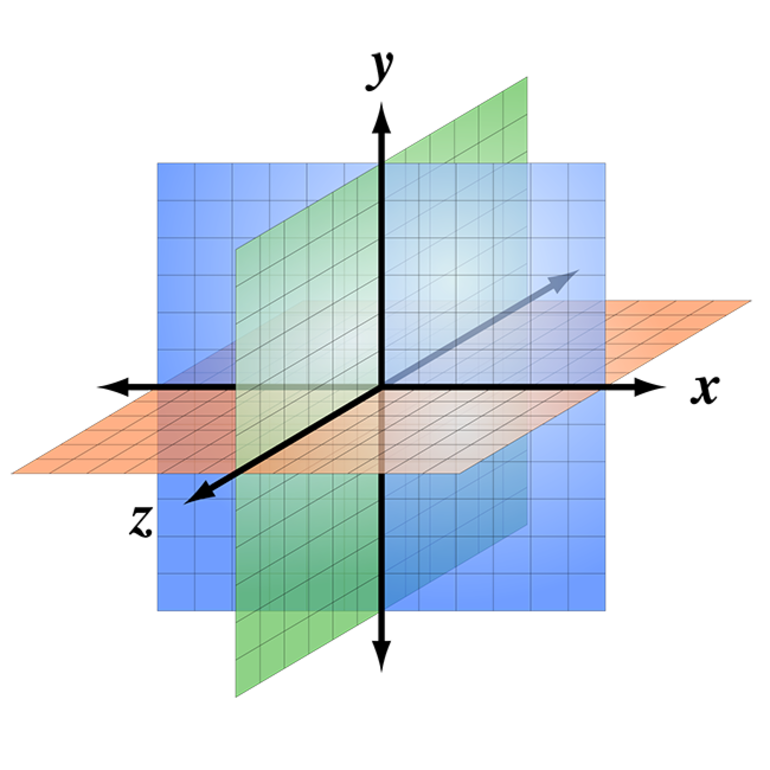
Трехмерное пространство

В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:

В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.

Четырехмерная система координат и лемма

Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.

Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:

Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.

Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:

При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.

Применение термина

Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.

В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.

В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.

Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.

Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.

Источник