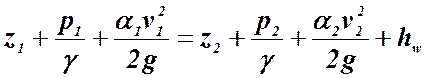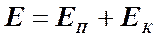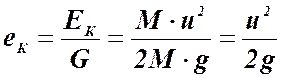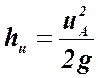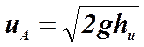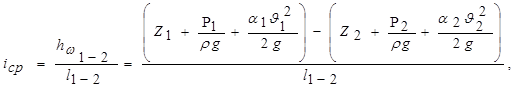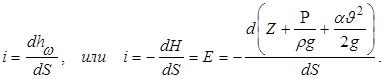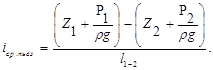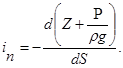Что такое пьезометрический уклон

Большая Энциклопедия Нефти и Газа

Пьезометрический уклон

Из определения гидравлического уклона следует, что гидравлический уклон мыслим только в вязкой жидкости и всегда направлен в сторону движения жидкости, так как потеря напора по длине неуклонно возрастает. Пьезометрический уклон может быть направлен как в сторону движения, так и в сторону, противоположную-1 движению. [32]

Знак минус здесь показывает, что имеет место действительное понижение напорной линии. Пьезометрическим уклоном называется падение потенциальной энергии на единице длины. [33]

Очевидно, при статическом расчете основания плотины необходимо знать сдвигающую силу, развиваемую потоком. Эта сдвигающая сила зависит от величины пьезометрических уклонов J в разных точках основания. [36]

Пьезометрическая линия при неравномерном плавно изменяющемся движении жидкости ( при распределении давлений в поперечных сечениях по гидростатическому закону) совпадает со свободной поверхностью потока. При неравномерном движении гидравлический уклон /, пьезометрический уклон и уклон дна потока гд в общем случае не равны между собой. [37]

Гидравлический уклон мыслим только в вязкой жидкости. Он всегда направлен в сторону движения, так как потеря энергии по длине неуклонно возрастает. Пьезометрический уклон также связан с потерей энергии. Обычно он направлен в сторону движения. Но в тех случаях, когда живые сечения струйки по течению увеличиваются в результате перехода кинетической энергии в потенциальную, пьезометрические уклоны могут иметь направление, обратное движению. [42]

Источник

Уклоны: геометрический, пьезометрический и гидравлический

Геометрическим уклоном называется падение геометрической линии струйки или потока жидкости на единицу длины. Для элементарной струйки, показано на рис. 3.8, на участке длиной l между сечениями 1-1 и 2-2 полное падение геометрической линии S-S равно разности геометрических высот .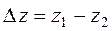

Средний геометрический уклон на

Рис. 3.8 этом участке равен

. (3.41)

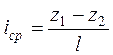
В случае, когда геометрическая линия криволинейна

. (3.42)

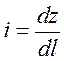
За геометрическую линию напорных потоков (в трубах) обычно принимается их осевая линия.

Пьезометрическим уклоном называется падение пьезометрической линии П-П на единицу длины струйки или потока жидкости.

. (3.43)

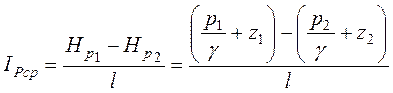
При криволинейной пьезометрической линии

. (3.44)

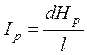
Гидравлическим уклоном называется падение напорной линии Н-Н на единицу длины струйки или потока жидкости

. (3.45)

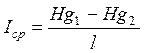
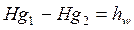
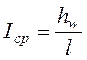
Так как, , то гидравлический уклон выражает так же потерю напора на единицу длины струйки или потока жидкости.

. (3.46)

При криволинейной напорной линии

. (3.47)

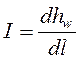
Следует отметить, что геометрический и пьезометрический уклоны в различных случаях могут быть и положительными и отрицательными. Гидравлический уклон всегда положителен.

Дата добавления: 2016-10-07 ; просмотров: 6073 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Равномерным движением называется такое установившееся движение, при котором живые сечения и скорости в сходственных точках живых сечений не изменяются по длине потока.

равномерное движение можно определить как движение, при котором все параметры потока и русла не изменяются по длине потока.

Неравномерным движением называется такое установившееся движение, при котором или живые сечения, или скорости в их сходственных точках, или оба эти признака меняются по длине потока.

3. Поясните понятия напорного и безнапорного движения жидкости

4. Поясните понятие линии тока

Линия тока это такая линия в потоке жидкости, в каждой точке которой в данный момент времени вектор скорости направлен по касательной к этой линии.

5. Поясните понятие живого сечения потока

Живым сечением потока называется поверхность внутри потока, которая нормальна ко всем пересекаемым ею линиям тока.

6. Поясните понятия плавно и резко изменяющегося движения жидкости

Плавно изменяющимся движением называется такое движение, при котором лини тока характеризуются малой кривизной и малыми углами схождения или расхождения

7. Что такое расход жидкости, и какова его единица измерения?

расходом (Q) называется объем жидкости, протекающий через рассматриваемое живое сечение в единицу времени.

где W – объем жидкости, а t время. Единица измерения расхода м3/с.

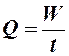
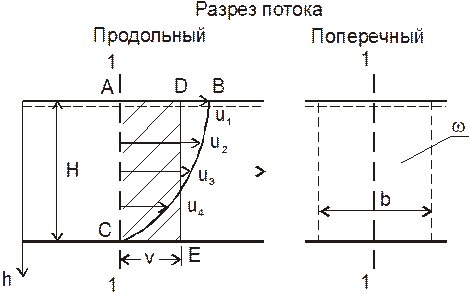
8. Нарисуйте эпюру распределения скоростей по глубине в открытом потоке жидкости

9. Поясните понятие средней скорости потока жидкости

средняя скорость потока равна частному от деления расхода на площадь живого сечения.

,

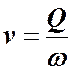
10. Объясните значение и назовите единицы измерения величин, входящих в формулу V=Q/o

V- средняя скорость потока ждкость

11. Напишите уравнение неразрывности потока и поясните его смысл

при установившемся движении потока несжимаемой жидкости расход во всех живых сечениях одинаков, или, иначе говоря, расход не изменяется по длине потока.

12. При каком виде движения жидкости соблюдается уравнение неразрывности потока?

При равномерном, установившемся

13. Напишите уравнение Бернулли и объясните его энергетический (физический) смысл

— полная удельная потенциальная энергия жидкости в живом сечении потока, взятая по весу,

— удельная потенциальная энергия давления,

— удельная кинетическая энергия,

— потеря энергии на участке потока 1-2.

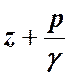
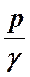
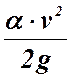
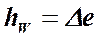
14. Напишите уравнение Бернулли и объясните геометрический смысл его членов

— скоростной напор,

— потенциальный напор,

— полный напор

— универсальное выражение полного гидравлического напора. Пользуясь понятием полного напора, уравнение Бернулли можно записать сокращенно в виде

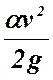
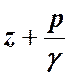
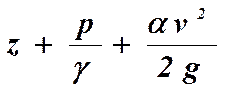
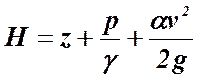
15. Как выражена в уравнении Бернулли удельная кинетическая энергия жидкости?

Удельная кинетическая энергия

16. Как выражена в уравнении Бернулли удельная потенциальная энергия жидкости?

17. Поясните физический смысл понятия напора жидкости и назовите единицу измерения напора

В гидравлике удельная энергия жидкости, взятая по весу, (энергия единицы веса жидкости) называется напором и обозначается Н.

18. Поясните физический смысл понятия «потери напора»

Энергия, затраченная на преодоление сил трения на перемещение жидкости по турбопроводу.

19. Напишите выражение полного напора жидкости из уравнения Бернулли

— полный напор

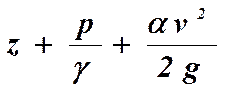
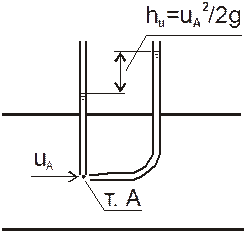
20. Как определить скорость движения жидкости с помощью трубки Пито?

21. Что такое напорная линия?

Напорная линия представляет собой график изменения напора по длине потока.

22. Что такое пьезометрическая линия?

пьезометрической линией называется линия, соединяющая уровни жидкости в пьезометрах.

23. Что такое пьезометрический уклон?

пьезометрический уклон это изменение потенциальной энергии потока на единице его длины.

24. Что такое гидравлический уклон?

гидравлический уклон это потеря напора на единице длины потока.

25. Как называется величина р/ γ в уравнении Бернулли?

— пьезометрическая высота,

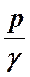
26. Как называется величина a*V 2 /2g в уравнении Бернулли?

— скоростная высота.

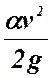
27. Какой уклон в гидравлике считается положительным и почему гидравлический уклон всегда положителен?

Гидравлический уклон всегда направлен вниз по течению потока. Иначе говоря, напорная линия всегда понижается в направлении течения, потому что часть напора (часть энергии потока) теряется на преодоление сопротивлений движению (сил трения). Уклон, направленный вниз по течению считается положительным. Таким образом, напорная линия всегда имеет положительный уклон.

28. Как называется а в выражении aV 2 /2g и каков физический смысл этой величины?

В уравнении Бернулли вместо скорости в точке u используется средняя скорость потока v и некоторая дополнительная величина α. Суть этих различий заключается в том, что в уравнении Бернулли скорость в точке намеренно заменена средней скоростью потока для упрощения гидравлических расчетов. Эта замена вызывает некоторую ошибку, которая ликвидируется поправочным коэффициентом α. Этот коэффициент учитывает неравномерность распределения скоростей в живых сечениях потока и называется коррективом кинетической энергии потока.

29. Начертите напорную и пьезометрическую линии при равномерном движении жидкости в напорной трубе

30. Начертите напорную и пьезометрическую линии при равномерном движении жидкости в открытом канале

31. Начертите напорную и пьезометрическую линии при неравномерном движении жидкости в открытом канале

Блок 5. Режимы движения жидкости и Лабораторная работа №5

1. Поясните физическую сущность ламинарного и турбулентного режимов движения жид­кости.

При ламинарном движении жидкость в процессе движения не перемешивается, а при турбулентном движении перемешивается.

2. Для чего употребляется число Рейнольдса в гидравлических расчетах?

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Гидравлический и пьезометрический уклоны

Для характеристики относительного изменения полного напора по длине потока введем понятие о гидравлическом уклоне.

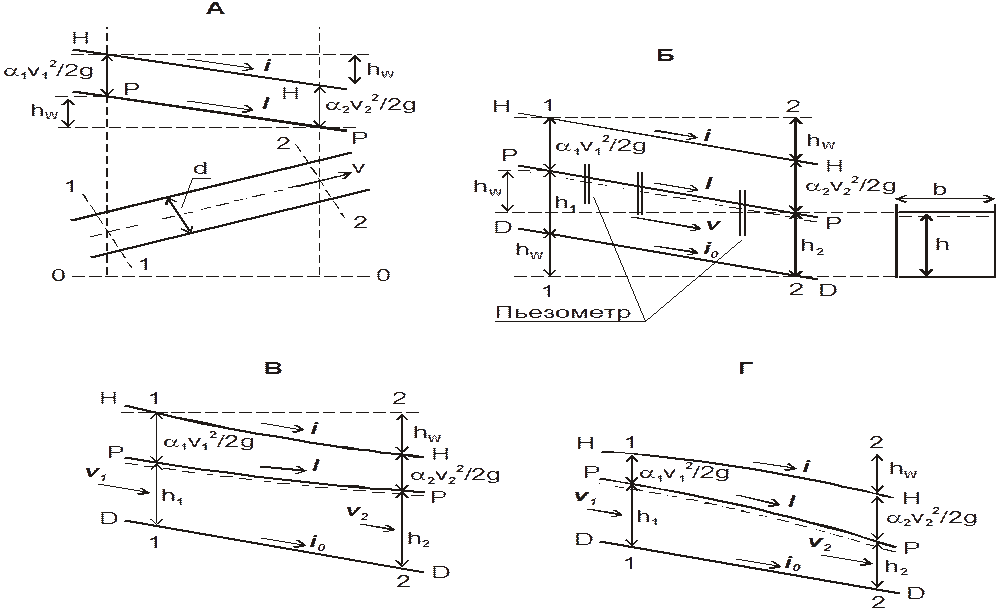
Среднее значение гидравлического уклона на участке потока между сечениями 1–1 и 2–2 (рис.6) определяется как отношение потери напора к длине участка:

где 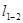− расстояние (по пути движение потока жидкости) между сечениями 1–1 и 2–2.

Гидравлический уклон −величина безразмерная и всегда больше нуля. В общем случае величина гидравлического уклона по длине потока переменная и в данном сечении потока определяется выражением

Здесь знак «минус» указывает на убывание полного напора по пути движения жидкости.

Понятие об уклоне можно ввести и для пьезометрической линии.

Средний пьезометрический уклон определяется по формуле

Значение пьезометрического уклона для некоторого сечения потока определяется выражением

Пьезометрический уклон может быть положительным, равным нулю и отрицательным

В случае, изображенном на рис. 4, пьезометрический уклон отрицательный, а на рис. 6 – положительный.

Источник

Тема 21 Уравнение Бернулли для потока конечных размеров. Гидравлический и пьезометрический уклоны

В случае плавно изменяющегося движения, при котором линии тока параллельны или почти параллельны, а кривизна струек незначительна, уравнение Бернулли, составленное для элементарной струйки, можно распространить на поток с поперечным сечением конечных размеров. Поток рассматривается при этом как совокупность элементарных струек, движущихся с различными скоростями. В таком потоке скорости в разных точках поперечного сечения различны, а скоростной напор, определяемый средней скоростью v, дополнен коэффициентом кинетической энергии (или коэффициентом Кориолиса) a. Величина этого коэффициента отражает степень неравномерности распределения скоростей по сечению потока. Коэффициент равен отношению истинной кинетической энергии массы жидкости, протекающей через живое сечение, к кинетической энергии, вычисленной в предположении, что во всех точках живого сечения местные скорости равны средней скорости.

Обычно при прямолинейном турбулентном движении в трубах a = 1,03…1,1. Обычно при расчётах при турбулентном течении в трубах принимают коэффициент Кориолиса a равным 1,1 или 1. При прямолинейном ламинарном движении в трубах a = 2.

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме давлений имеет вид:

r × g × z + р + r × a × 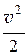= const, (21.1, а)

где r × g × z – гравитационное давление;

р – статическое давление;

r × 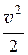– динамическое давление.

Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

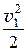
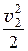
r × g × z₁ + р₁ + r × a₁ × = r × g × z₂ + р₂ + r × a₂ × = const. (21.1, б)

Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости в форме напоров имеет вид:

z + 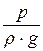+ a× = Н = const, (21.2, а)

где z – удельная потенциальная энергия положения;

– удельная потенциальная энергия давления;

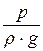
a × – удельная кинетическая энергия (динамический напор для потока);

Н – полная удельная энергия потока.

Таким образом, полная удельная энергия потока, так же, как и для элементарной струйки, есть сумма удельной потенциальной энергии 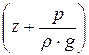и удельной кинетической энергии a × .

Для двух произвольных сечений 1-1 и 2-2 уравнение имеет вид:

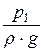
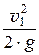
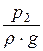
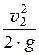
z₁ + + a₁ × = z₂ + + a₂ × = Н = const. (21.2, б)

С энергетической точки зрения уравнение Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.

Все члены уравнения Бернулли имеют линейную размерность и их можно интерпретировать как высоты:

z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;

= – высота давления. Если в уравнении р – избыточное давление, то величина

= называется пьезометрической высотой;

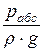
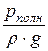
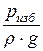
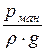
a × – скоростная (или динамическая) высота.

Н = – полная высота в данном сечении потока.

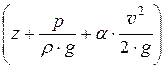
Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль потока сумма высот – положения, давления (или пьезометрической) и скоростной – есть величина постоянная.

Уравнение Бернулли для установившегося движения вязкой несжимаемой жидкости между двумя сечениями, в которых движение является плавно изменяющимся, имеет вид:

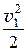
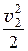
r × g × z₁ + р₁ + r × a₁ × = r × g × z₂ + р₂ + r × a₂× + Dр, (21.3)

где Dр – потери давления на участке между рассматриваемыми сечениями;

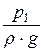
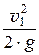
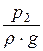
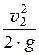
z₁ + + a₁× = z₂ + + a₂ × + Dh_пот, (21.4)

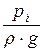
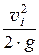
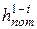
z_i + + a_i × + D = Н = const.

где Dh_пот – потери напора на участке между рассматриваемыми сечениями.

Для потока жидкости сумма удельной потенциальной и удельной кинетической энергии

Н = 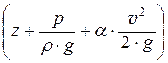(21.5)

называется гидродинамическим (или полным) напором.

При движении вязкой жидкости линия удельной энергии (напорная линия) не горизонтальна, как при движении невязкой жидкости, а представляет собой наклонную линию, так как удельная энергия потока (гидродинамический напор) Е = Н = 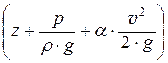при движении вязкой жидкости уменьшается в направлении движения.

Энергетический смысл уравнения Бернулли для потока вязкой жидкости:

удельная энергия потока в предыдущем сечении всегда больше чем в последующем на величину потерь удельной энергии.

Геометрический смысл уравнения Бернулли для потока вязкой жидкости:

полная высота в предыдущем сечении всегда больше чем в последующем на высоту потерь Dh_пот.

Гидравлическим уклоном i называется отношение потерь напора Dh_тр к длине участка l, на котором эти потери происходят:

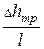
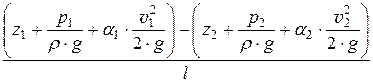
i = = > 0. (21.6, а)

Так как приращение dH всегда является отрицательным (напор уменьшается вдоль движения), то гидравлический уклон всегда положителен.

Удельная потенциальная энергия 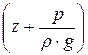(пьезометрический напор) в направлении движения может, и уменьшатся, и увеличиваться, в зависимости от конкретных условий.

Пьезометрическим уклоном i_п называется отнесённое к единице длины изменение пьезометрического напора 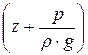или изменение отметок пьезометрической линии. В общем случае

Для двух сечений имеем

i_п = 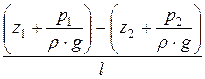. (21.7, б)

Пьезометрический уклон может быть положительным, отрицательным и равным нулю. Пьезометрический уклон считается положительным, если по течению пьезометрическая линия понижается.

Дата добавления: 2015-08-26 ; просмотров: 1329 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник