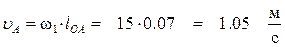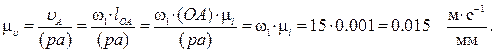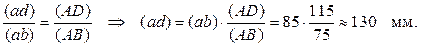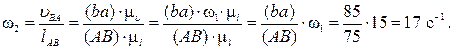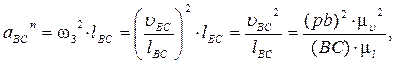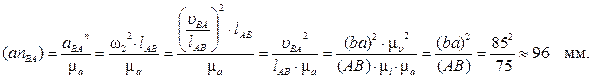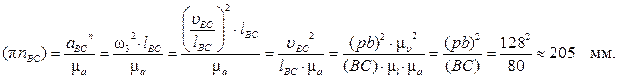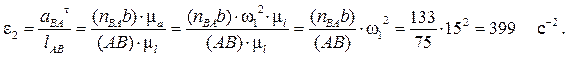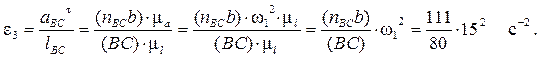Что такое план механизма

Лекция 8. Тема: Построение планов скоростей и ускорений механизма, образованного группой Ассура 2–го класса 1–го вида.

Тема: Построение планов скоростей и ускорений механизма, образованного группой Ассура 2–го класса 1–го вида.

Построение плана скоростей

Планы скоростей и ускорений механизма строятся после решения задачи о его положении, причём построение планов проводится для отдельных групп Ассура, которые образовали механизм. Вначале строится план скоростей (ускорений) группы, которая присоединена элементами своих внешних кинематических пар к ведущему звену и стойке, затем строятся планы скоростей (ускорений) второй и т.д. групп, взятых в той же последовательности, в какой они присоединяются при образовании механизма.

Рассмотрим двухкривошипный шарнирный четырёхзвенник. Данные: l_OA = 0.07 м, l_OC = 0.04 м, l_BC = 0.08 м, l_AB = 0.075 м, l_BD = 0.04, j₁ = 30°, угловая скорость кривошипа OA постоянна и равна w₁ = 15 c – 1 (рис. 1).

План положения механизма

Сначала строим план заданного положения механизма. Масштаб длин принимаем равным m_l = 0.001 м /мм. Вычисляем длины отрезков, изображающие на чертеже звенья.

Для каждого положения механизма определяются скорости точек графическим методом. Вначале определяем скорость точки A, принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью w₁. Скорость этой точки по модулю равна

и направлена перпендикулярно оси звена OA в сторону вращения. Отложим от произвольной точки p, называемой полюсом плана скоростей, отрезок (pa). Длину отрезка (pa) выбираем равной (OA). (pa) = (OA) = 70 мм. Вычисляем масштабный коэффициент скоростей:

Строим план скоростей для группы звеньев 2 и 3. Оба звена совершают плоскопараллельное движение. Из теоретической механики известно, что скорость любой точки B плоской фигуры геометрически складывается из скорости какой-нибудь точки A, принятой за полюс, и скорости, которую точка B получает при вращении фигуры вокруг этого полюса.В этой группе звеньев все пары вращательные. Определяем скорость точки B по следующим двум векторным уравнениям:

Определяем скорость точки B: u_B = (pb)×m_u = 128×0.015 = 1.92 м/c.

Определяем скорость точки D: u_D = (pd)×m_u = 169×0.015 » 2.54 м/c.

Определяем угловую скорость звена AB:

План скоростей механизма

Направление угловой скорости w₂ звена AB может быть определено следующим образом. Мысленно прикладывая вектор к точке B, видим, что вращение звена 2 вокруг оси шарнира A, принятой за полюс, совпадает с направлением вращения часовой стрелки. Отмечаем нужное направление вращения на звене 2 в виде дуговой стрелки.

Определяем угловую скорость звена BC:

Направление угловой скорости w₃ звена BC определяется таким же образом, как и w₂. Мысленно прикладывая вектор к точке B, видим, что вращение звена 3 вокруг оси шарнира C, принятой за полюс, совпадает с направлением вращения часовой стрелки. Отмечаем нужное направление вращения звена 3 дуговой стрелкой.

Построение плана ускорений

Ускорения точек находятся методом плана ускорений. Вначале определяем скорость точки A, принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью w₁. Полное ускорение точки A определяется по формуле Так как e₁ = 0, то тангенциальное ускорение a t _A = 0. Тогда и ускорение точки A легко вычисляется: a_A = w₁ 2 ×l_OA. Затем строим план ускорений для группы звеньев 2 и 3. Так как движение этих звеньев плоское и все пары вращательные, то используем известную из теоретической механики теорему: ускорение любой точки B плоской фигуры геометрически складывается из ускорения какой-нибудь точки A, принятой за полюс, и ускорения, которое точка B получает при вращении фигуры вокруг этого полюса. Этот план строится по таким двум векторным уравнениям:

где — полное ускорение точки A, равное нормальному ускорению , так как звено 1 (кривошип) вращается равномерно и угловое ускорение равно нулю, следовательно равно нулю и тангенциальное ускорение ,

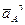
и направленное параллельно линии OA от точки A к точке O (к центру кривизны траектории);

— нормальное ускорение точки B во вращательном движении звена AB вокруг точки A, по модулю равное

и направленное параллельно линии AB от точки B к точке A ( );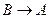

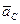
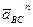
— тангенциальное ускорение точки B в том же движении звена AB, по модулю равное

— ускорение точки C, равное нулю, так как звено 4 неподвижно;

— нормальное ускорение точки B во вращательном движении звена BC вокруг точки C, по модулю равное

и направленное параллельно линии BC от точки B к точке C ( );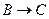

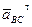
— тангенциальное ускорение точки B в том же движении звена BC, по модулю равное

Построение плана ускорений ведём в следующей последовательности. Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана p откладываем отрезок (pa), изображающий ускорение 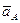, параллельно линии OA. Длину отрезка (pa) принимаем равной 70 мм, отчего масштаб ускорений будет

От точки a откладываем отрезок (an_BA), изображающий ускорение . Длина отрезка (an_BA) вычисляется так:

Через точку n_BA проводим направление ускорения — линию, перпендикулярную линии AB. Переходим к построению решения второго векторного уравнения, указанного выше. Для этого от полюса плана p откладываем вектор ускорения , но оно равно нулю, поэтому точка c совпадает с точкой p. От точки p откладываем отрезок (pn_BC), изображающий ускорение . Длина отрезка (pn_BC) вычисляется так:

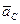
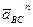
Соединив точку d с полюсом плана p, получаем отрезок (pd), изображающий абсолютное ускорение точки D.

Величины абсолютных ускорений точек B и D определяются так:

По правилу подобия найдём ускорения центров масс подвижных звеньев. Точки S₁, S₂ и S₃ находятся на серединах соответствующих звеньев. На плане ускорений это будут векторы: (ps₁), (ps₂) и (ps₃). Определяем абсолютные величины ускорений этих центров масс:

Величина углового ускорения звена AB равна:

Направление углового ускорения e₂ звена 2 (звена AB) может быть определено следующим образом. Перенося мысленно вектор 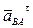в точку B, видим из точки A, что направление e₂ совпадает с направлением вращения часовой стрелки. Обозначаем направление углового ускорения e₂ на плане положения звена 2 дуговой стрелкой.

Величина углового ускорения звена BC равна:

Направление углового ускорения e₃ звена 3 (звена BC) может быть определено таким же образом, как и e₂. Перенося мысленно вектор 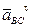в точку B, видим из точки C, что направление e₃ совпадает с направлением вращения часовой стрелки. Обозначаем направление углового ускорения e₃ на плане положения звена 3 дуговой стрелкой. План ускорений механизма приведён на рис. 3.

Источник

Что такое план механизма

Относительная скорость [TEX]V_ [/TEX] – скорость относительного движения.

Относительное ускорение [TEX]a_ [/TEX] – ускорение относительного движения.

Период цикла [TEX]T[/TEX] – время, после истечения которого звенья занимают исходное положение.

Аналог скорости точки [TEX]\frac<\texts_ ><\textφ_ <1>> [/TEX] – первая производная радиуса-вектора точки по обобщенной координате механизма [TEX]φ_ <1>[/TEX].

Аналог ускорения [TEX]\frac s> [/TEX] – вторая производная радиуса-вектора точки по обобщенной координате механизма [TEX]φ_ <1>[/TEX].

Передаточное число [TEX]u[/TEX] – отношение числа зубьев большего колеса [TEX]Z_ <2>[/TEX] к числу зубьев меньшего колеса [TEX]Z_ <1>[/TEX] (шестерни).

4.1.2 Планы механизмов

Фазовый угол рабочего движения [TEX]φ_ <р>[/TEX] – угол поворота входного звена (кривошипа), соответствующий рабочему движению.

Фазовый угол холостого движения [TEX]φ_ <х>[/TEX] – угол поворота входного звена (кривошипа), соответствующий холостому движению.

Коэффициент углового перемещения [TEX]k_ <φ>[/TEX] – это величина, определяемая выражением [TEX]k_<φ>=φ_<р>/φ_\geq 1 [/TEX].

Коэффициент изменения средней скорости [TEX]k_ [/TEX] – это величина, определяемая выражением [TEX]k_=V_<р>/V_\leq 1 [/TEX], где [TEX]V_ <р>[/TEX], [TEX]V_ [/TEX] – средняя скорость выходного звена, соответствующая холостому и рабочему движениям механизма.

4.1.3 Исследование кинематики

Теорема подобия плана скоростей (ускорений): векторы относительных скоростей (ускорений) точек звена на плане скоростей (ускорений) образуют фигуру, подобную фигуре, образованной отрезками, соединяющими эти точки на звене.

4.2 Принципы кинематического исследования механизмов

4.2.1 Основные кинематические характеристики

4.2.2 Цель, задача и методы кинематического исследования

Целью кинематического исследования является изучение движения звеньев механизма без учета сил, действующих на них. На основе полученных результатов оценивают кинематические свойства выбранной схемы механизма и в случае необходимости в него вносят коррективы.

Основные задачи кинематического исследования:

Исследования выполняют в той же последовательности, что и образование структурной схемы механизма, то есть сначала для механизма первого класса, а затем для каждой структурной группы Ассура.

4.2.3 Алгоритм кинематического исследования

На рисунке 4.1 показана принципиальная схема кинематического исследования механизма.

4.3 Аналитический метод кинематического исследования

Сущность этого метода рассмотрим на примере исследования плоского кривошипно-ползунного механизма (рисунок 4.2).

Задача заключается в установлении зависимостей вида:

Выразим угол [TEX]\alpha [/TEX] через известные параметры, после некоторых преобразований получим приблизительную формулу для определения перемещений ползуна:

Дважды дифференцируя выражение (4.1), будем иметь:

На основании полученных формул (4.1), (4.2) и (4.3) можно построить кинематические диаграммы перемещений, скорости и ускорений точки [TEX]C[/TEX], то есть графики функций [TEX]S_ =f(φ_<1>)[/TEX], [TEX]S_=f(t)[/TEX], [TEX]V_=f(φ_<1>)[/TEX] и [TEX]a_=f(φ_<1>) [/TEX] рисунок 4.3.

4.4 Графоаналитический метод кинематического исследования

4.4.1 Построение планов положений механизмов

Выбираем масштабный коэффициент (масштаб) длин:

где [TEX]l_A > [/TEX] – истинная длина кривошипа, м;

[TEX]O_<1>A [/TEX] – длина отрезка, изображающего кривошип на плане механизма, мм.

Длины отрезков остальных звеньев на схеме механизмов получаем делением настоящих длин звеньев на масштабный коэффициент [TEX]\mu _ [/TEX].

Радиусом [TEX]O_<1>A [/TEX] изображаем окружность с центром в точке [TEX]O_ <1>[/TEX]. С учетом масштаба [TEX]\mu _ [/TEX] на чертеже находим геометрические места неподвижных осей вращения [TEX]O_ <1>[/TEX], [TEX]O_ <2>[/TEX].

Оцениваем значения фазовых углов [TEX]φ_ <г>[/TEX] и [TEX]φ_ <х>[/TEX] рабочего и холостого хода и коэффициент неравномерности движения механизма [TEX]k_<φ>=φ_<г>/φ_ <х>[/TEX].

Если [TEX]φ_<г>=φ_ <х>[/TEX], то [TEX]k_<φ>=1[/TEX] и между мертвыми положениями механизма угол поворота составляет [TEX]180^ <\circ >[/TEX]. Это характерно, например, для кривошипно-шатунных механизмов, в которых ось вращения кривошипа и линия движения ползуна лежат на одной прямой. Для подобных механизмов не имеет значения по ходу часовой стрелки или против выбраного направления вращения кривошипа.

Если [TEX]k_<φ>>1 [/TEX], то направление движения кривошипа выбираем с соблюдением следующего условия: сила полезного (технологического) сопротивления должна быть приложенна к выходному звену в фазе рабочего движения. Важно, что при этом коэффициент изменения средней скорости равен [TEX]k_<φ>=V_<г>/V_ <х>1[/TEX] строим тринадцать положений, второе мертвое положение может быть между шестым и седьмым (положение [TEX]6′[/TEX]) или между седьмым и восьмым (положение [TEX]7′[/TEX]).

Будем считать, что [TEX]\omega _<1>=const[/TEX].

Необходимо определить скорости и ускорения точек звеньев.

Решение задачи может быть выполнено:

Для звена [TEX]AB[/TEX] (рисунок 4.5), что выполняет вращательное движение, имеем [TEX]V_=\omega _<1>l_ <1>[/TEX].

Для текущей точки [TEX]i[/TEX] и [TEX]V_=\omega _<1>l_ [/TEX], [TEX]0\leq l_\leq l_ <1>[/TEX].

Ускорение этой точки – [TEX]a_=c_i^n=V_i^2/l_=\omega _i^2l_ [/TEX].

Поскольку [TEX]\omega _<1>=const[/TEX], то [TEX]ε_<1>=\frac<\text\omega _ <1>><\textt>=0 [/TEX] и [TEX]a_i^\tau =ε_<1>l_=0[/TEX].

Для звена [TEX]BC[/TEX] (рисунок 4.6 а), находящегося в плоскопаралельном движении, линейные скорости любой его точки легко определить, если использовать понятие мгновенного центра скоростей.

Из рисунка 4.6 а следует, что угловая скорость шатуна [TEX]\omega _<2>=V_/P_B [/TEX], причем [TEX]V[/TEX] известно из предыдущего рисунка, поскольку точка [TEX]B[/TEX] одновременно принадлежит и шатуну и кривошипу.

Тогда скорость точки [TEX]C[/TEX] и [TEX]\overline>=\overline<\omega _<2>> P_C [/TEX], а скорость любой точки [TEX]K[/TEX] звена [TEX]BC[/TEX] и [TEX]\overline>=\overline<\omega _<2>>P_K [/TEX] (рисунок 4.6 б).

Следовательно, для определения скоростей точек звена необходимо знать скорость одной точки и направление скорости второй.

Однако использование мгновенных центров скоростей звеньев сложного механизма громоздко, поэтому в дальнейшем рассматриваемую задачу будем решать методом планов скоростей (ускорений).

Этот метод используют для определения модуля и направления скоростей и ускорений исследуемых точек и звеньев механизма. Он рассматривался в курсе теоретической механики. Сущность метода заключается в следующем.

Для построения плана скоростей (ускорений) любой звена [TEX]BC[/TEX] будем использовать две теоремы теоретической механики:

Следовательно, движение звена [TEX]BC[/TEX] в подвижной системе координат [TEX]x_ <1>y_ <1>z_ <1>[/TEX] является вращательным, причем в качестве центра вращения можно брать любую точку (желательно точку [TEX]B[/TEX], скорость которой известна).

Представляя любое движение звеньев, в частности и плоское, как сложное, состоящее из двух движений: переносного и относительного, записываются соответствующие векторные уравнения скоростей и ускорений точек, которые исследуются.

Важно отметить, что, имея планы скоростей и ускорений, можно легко определить угловые скорости [TEX]\omega [/TEX] и угловые ускорения [TEX]ε[/TEX] звеньев.

Для каждой двуповодковой структурной группы Ассура можно составить два векторных уравнения, связывающие скорость (ускорение) исследуемой точки с известными скоростями (ускорениями) двух других точек. Эти уравнения решаются совместно графически путем построения планов скоростей и ускорений, то есть картины мгновенных скоростей и ускорений отдельных точек звеньев механизма для его конкретного положения. Отсюда следует, что решение задачи следует начинать с построения планов положений механизма.

4.4.2 Построение плана скоростей

Построим план скоростей для одного положения, любого механизма, например кривошипно-коромыслового (рисунок 4.8 б).

Из кинематической схемы механизма видно, что при вращении кривошипа [TEX]AB[/TEX] коромысло (балансир) [TEX]CD[/TEX] может осуществлять или вращательное или возвратно-вращательное движение (в зависимости от соотношения длин звеньев).

Из полюса [TEX]P_ [/TEX] откладываем отрезок [TEX]pb[/TEX] в соответствии с выбранным масштабным коэффициентом [TEX]\mu _ [/TEX]. Направление отрезка [TEX]pb[/TEX] совпадает с направлением линейной скорости точки [TEX]B[/TEX] звена 1 на плане механизма.

Точка [TEX]C[/TEX] принадлежит звену 2 и звену 3 одновременно и совершает вращательные движения относительно точек [TEX]B[/TEX] и [TEX]D[/TEX]. В относительном движении скорость [TEX]V_ [/TEX] перпендикулярна звену 2 (т.е. известна линия действия). Аналогично скорость [TEX]V_ [/TEX] перпендикулярна звену 3 (известна линия действия).

Для определения величины и направления скорости точки [TEX]C[/TEX] состовляют два векторных уравнения в следующей форме:

[TEX]\begin\overrightarrow > = \overrightarrow>+\overrightarrow>\perp CB \\\overrightarrow>=\overrightarrow>+\overrightarrow>\perp CD\end [/TEX](4.5)

На основе записанных уравнений строим план скоростей. К вектору [TEX]pb[/TEX] проводим линию действия скорости [TEX]V_ [/TEX] перпендикулярно звену [TEX]BC[/TEX]. Поскольку скорость точки [TEX]D[/TEX] [TEX]V_=0[/TEX], то линию действия скорости [TEX]V_ [/TEX] проводим через полюс плана скоростей. На пересечении линий действия скоростей [TEX]V_ [/TEX] и [TEX]V_ [/TEX] получим точку [TEX]C[/TEX], которая определит направление скорости точки [TEX]C[/TEX]. Кроме того, с помощью построенного плана скоростей определяются величины относительных и абсолютных скоростей через соответствующие отрезки:

Угловые скорости звеньев 2 и 3 определяются по уравнению:

Для схемы, приведенной на рисунке 4.9, определение линейных и угловых скоростей соответствует вышеприведенной методике. Для определения скорости точки [TEX]E[/TEX] рассмотрим ее движение относительно точки [TEX]B[/TEX] и [TEX]C[/TEX]. Для этого допишем векторные уравнения:

[TEX]\overrightarrow >=\overrightarrow>+\overrightarrow>\perp BE[/TEX],

[TEX]\overrightarrow >=\overrightarrow >+\overrightarrow >\perp EC[/TEX].(4.7)

Решая графически эти уравнения, получим соответствующий план скоростей (смотри рисунок 4.9 б).

4.4.3 Основные свойства плана скоростей

На основании результатов кинематического исследования, полученных выше, можно сформулировать следующие свойства плана скоростей:

4.4.4 Построение плана ускорений

Сущность метода заключается в том, что векторные уравнения для ускорений точек звеньев решаются графическим путем.

Определение линейных ускорений точек и угловых ускорений звеньев выполняется на основании векторных уравнений с помощью построенного плана ускорений.

Проведем анализ движения звеньев механизма (рисунок 4.10 а). Звено 1 совершает вращательное движение вокруг точки [TEX]A[/TEX], звено 2 совершает плоскопаралельное движение (поступательное и вращательное), звено 3 совершает вращательное движение вокруг точки [TEX]D[/TEX]. В общем случае для звена, совершающего вращательное движение, ускорение точки [TEX]a_ [/TEX] имеет две составляющие: нормальную и тангенциальную. Нормальная составляющая направлена к центру вращения, тангенциальное направлена перпендикулярно нормальной. Для схемы механизма, приведена на рисунке 4.10 а, ускорение точки [TEX]B[/TEX] находится по формуле:

В свою очередь, величина ускорения:

​Тангенциальное ускорение определяется по формуле:

Если принять, что звено 1 вращимся равномерно, то [TEX]ε_<1>=0[/TEX], тогда полное ускорение точки [TEX]B[/TEX] в отношении [TEX]A[/TEX] будет равно нормальной составляющей:

Ускорения других точек звеньев определяются по векторным уравнением с помощью построенного плана ускорений. Точка [TEX]C[/TEX] принадлежит звеньям 2 и 3. Тогда полное ускорение точки [TEX]C[/TEX] определяется следующим образом:

Нормальная составляющая [TEX]a_^n [/TEX] звена 2 направлена от точки [TEX]C[/TEX] вдоль звена к точке [TEX]B[/TEX]. Ускорение [TEX]a_^n [/TEX] для звена 3 направлено вдоль звена к точке [TEX]D[/TEX].

Значение этих ускорений находятся по формуле:

Тангенциальные (касательные) составляющие определяются с помощью плана ускорений. Для этого из точки [TEX]p[/TEX] – полюса плана ускорений (рисунок 4.10 б) откладываем отрезок [TEX]pb[/TEX], соответствующий направлению ускорения точки [TEX]B[/TEX]. Определим масштабный коэффициент плана ускорений, [TEX]м\cdot с^<-2>/мм[/TEX].

Согласно уравнению 4.12 к концу вектора [TEX]pb[/TEX] добавляем вектор ускорения [TEX]a_^n [/TEX] в виде отрезка [TEX]bn_ <2>[/TEX], длина которого, мм, определится из условия выбранного масштабного коэффициента [TEX]\mu _ [/TEX].

Из построенного плана определяются направления и значения неизвестных ускорений, [TEX]мс^<-2>/мм[/TEX],

Поскольку известны нормальные и тангенциальные составляющие, то полные ускорения, [TEX]мс^<-2>/мм[/TEX], определяются следующим образом:

Ускорение центра масс звена, положение которого известно, определяется по теореме подобия.

С помощью плана ускорений определяются угловые ускорения, [TEX]рад/мм[/TEX], звеньев 2 и 3 из следующих выражений:

4.4.5 ​Основные свойства плана ускорений

4.5 Графический метод кинематического исследования

4.5.1 Графическое дифференцирование

При кинематическом исследовании механизмов скорости и ускорения точек и звеньев удобно выражать в виде функции угла поворота [TEX]φ[/TEX] начального звена, как показано на рисунке 4.11.

Исследование движения механизма может быть проведено с помощью диаграмм перемещений, скоростей и ускорений. Эти диаграммы строятся после кинематического анализа механизма для ряда достаточно близких положений механизма, соответствующих одному циклу (одному обороту начального звена [TEX]AB[/TEX]).

Определим одно из крайних положений ползуна и принимаем его за нулевое. Крайнее левое положение точки [TEX]C[/TEX] (рисунок 4.11 а) имеет место, когда шатун [TEX]BC[/TEX] наложится на кривошип [TEX]AB[/TEX] и совпадает с линией [TEX]AC[/TEX].

Строим 12 положений механизма, разделив заблаговременно круг с радиусом [TEX]AB[/TEX] на 12 равных частей (через каждые [TEX]30^ <\circ >[/TEX]). Перемещение ползуна [TEX]C[/TEX] 0-1, 0-2, 0-3 и так далее соответствуют положениям кривошипа 0, 1, 2, 3 и так далее. Диаграмма перемещений строится следующим образом. Проводим оси координат [TEX]S[/TEX] и [TEX]t[/TEX] или [TEX]S[/TEX] и [TEX]φ[/TEX]. Если кривошип вращается равномерно, то его угол поворота [TEX]φ[/TEX] пропорционален времени [TEX]t[/TEX]. На оси [TEX]φ[/TEX] откладываем 12 одинаковых отрезков 0-1, 1-2, 2-3 и так далее, соответствующие углу поворота кривошипа. Через точки 1, 2, 3. проводим ординаты и откладываем на них отрезки 1-1′, 2-2′, 3-3′ и так далее, которые равны соответствующим перемещением точки [TEX]S_ <1>[/TEX], [TEX]S_ <2>[/TEX], [TEX]S_ <3>[/TEX] и так далее. Соединяя точки 1-1′, 2′, 3′ и так далее, плавной кривой, получим диаграмму перемещений [TEX]S=S(φ)[/TEX]. Масштаб перемещений на диаграмме [TEX]\mu _ [/TEX], равен масштабу планов механизма, поскольку перемещения точки [TEX]C[/TEX] ползуна перенесены на диаграмму без изменений. Масштаб, 1/мм, по оси абсцисс равен:

где [TEX]|0-12|[/TEX] – отрезок, мм, изображающий полный оборот кривошипа [TEX](2\pi )[/TEX], которой выражен в миллиметрах.

Построение диаграммы [TEX]\frac<\texts><\textφ> [/TEX] проводим графическим дифференцированием методом хорд или методом касательных. Рассмотрим построение диаграммы [TEX]\frac<\texts><\textφ>-\frac<\texts><\textφ>(φ)[/TEX] методом хорд. Разделяем кривую [TEX]S=S(φ)[/TEX] на ряд участков 0-1, 1-2, 2-3, и так далее и заменяем кривые хордами (рисунок 4.11 б). Заменяем неравномерное движение ползуна на каждом участке равномерным. На оси [TEX]φ[/TEX] диаграммы [TEX]\frac<\texts><\textφ> [/TEX] влево от начала координат на произвольном расстоянии [TEX]H_ <1>[/TEX] выбираем точку [TEX]P_ <1>[/TEX] (рисунок 4.11). С этой точки проводим лучи P-1″, P-2″, P-3″, P-4″, параллельные соответствующим хордам 0-1′, 1′-2′, 2′-3′, и так далее. Эти лучи отсекают на оси [TEX]\frac<\texts><\textφ> [/TEX] отрезки 0-1″, 0-2″, 0-3″, и так далее, пропорциональные средним значениям скоростей или средним значением аналогов скоростей [TEX]\frac<\texts><\textφ> [/TEX] на соответствующих участках. Откладывая равные этим отрезкам координаты [TEX]y[/TEX], на соответствующих участках, получим ступенчатую линию 1″‘1″‘2″‘2″‘3″‘3″‘. Действительный график скорости или аналога скорости получим, если проведем плавную кривую через выступы ступенчатого графика (рисунок 4.11).

Масштабный коэффициент аналога скоростей определяется по формуле [TEX]\mu _<\frac<\texts><\textφ>>=\frac <\mu _> <\mu _<φ>H_<1>> [/TEX]. Определение ускорения точки [TEX]C[/TEX] или аналога ускорения [TEX]\fracs> > [/TEX] проводят аналогично определению скорости или аналога скорости, графически дифференцируя зависимость[TEX]\frac<\texts><\textφ> [/TEX] методом хорд (рисунок 4.11 г).

4.5.2 Графическое интегрирование

Пусть будет задан график аналога ускорения звена [TEX]\fracs> > [/TEX] (рисунок 4.12 а). Ось абсцисс разбиваем на несколько равных участков 0-1, 1-2, 2-3, 3-4 и так далее. На каждом участке проводим горизонтальные отрезки таким образом, чтобы площади треугольников слева и с права от кривой на интервале 0-1 оси абсцисс были равными. С некоторыми погрешностями эту задачу можно упростить. Берем середину интервала на оси абсцисс, проводим вертикальную линию (она на графике приведена пунктиром) до пересечения с кривой. Через эту точку проводят горизонтальную линию до пересечения с осью ординат и обозначают точкой 1″. Аналогичную операцию выполняют на интервале 1-2 оси абсцисс. На оси ординат находят точки 2″, 3″, 4″ и так далее. Выбираем слева от оси [TEX]\fracs> > [/TEX] произвольный отрезок [TEX]H[/TEX] и точку [TEX] [/TEX]. Соединив эту точку с точками 1″, 2″, 3″ и так далее, которые найденны на оси ординат, получаем лучи P-1″, P-2″, P-3″ и так далее.

Под заданной диаграммой проводим координатные оси [TEX]\frac [/TEX] и [TEX]φ[/TEX] (рисунок 4.12 б). Разбиваем ось абсцисс на участки так, как это сделано на графике [TEX]\fracs>>= \fracs>>(φ)[/TEX]. Далее на участке 0-1 проводим из начала координат отрезок 0-1′, параллельный лучу P-1″, из точки 1′ на участке 1-2 проводим отрезок 1′-2′, параллельный лучу P-3″ и так далее. Полученная ломаная линия представляет собой примерно график аналога скорости [TEX]\frac(φ)[/TEX] в масштабе. Для получения графика перемещений необходимо графически проинтегрировать полученный график, так, как это было выполнено для получения графика [TEX]\frac(φ)[/TEX]. Метод графического интегрирования противоположный методe графического дифференцирования.

Published by: Сергей Сергеевич Некрасов

RSS Feed

Источник