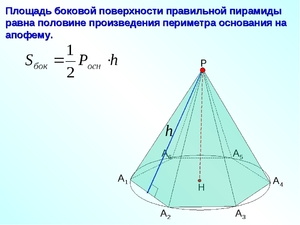
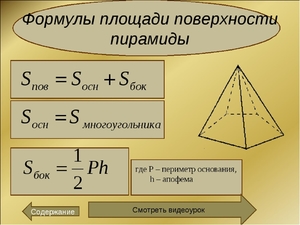
Что такое площадь боковой поверхности пирамиды

Формула площади боковой поверхности пирамиды произвольного типа и правильной: пример задачи

Каждый человек слышал о великих египетских каменных сооружениях, главным из которых является пирамида Хеопса. В курсе стереометрии рассматривают характеристики различных пирамид. Одним из важных параметров фигуры является площадь боковой поверхности. По какой формуле боковой поверхности площадь пирамиды следует рассчитывать, расскажет данная статья.

Что собой представляет пирамида в геометрии?

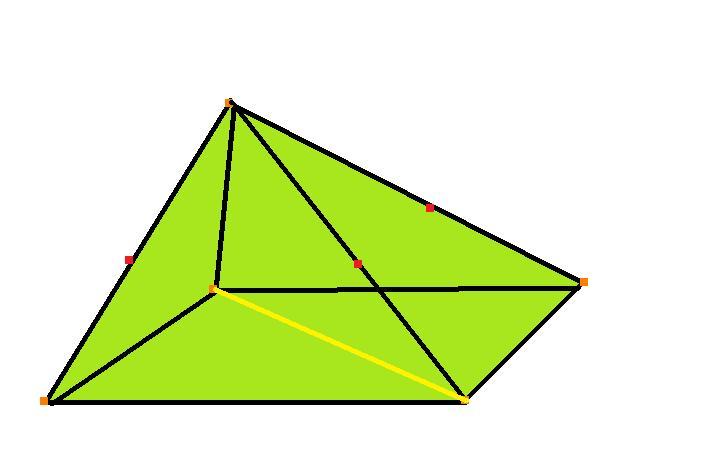
Прежде чем говорить о пирамиде и формуле площади боковой поверхности, дадим определение самой фигуры. Под ней полагают объемный многогранник, состоящий из одного n-угольного основания и n треугольников. Все треугольники имеют одну общую с основанием сторону, а также пересекаются в точке, которая называется вершиной. Ниже показана произвольная четырехугольная пирамида:

Вам будет интересно: Генералы чеченской войны: пофамильный список, краткая биография и фото

Любая пирамида состоит из:

Причем все названные элементы бывают двух типов: те, которые относятся к основанию, и те, которые принадлежат боковой поверхности.

Параметры боковой поверхности для фигуры произвольного типа

Как находить площадь (формула представлена ниже) поверхности боковой грани рассматриваемой фигуры? Ответить на этот вопрос несложно, если знать, что боковая поверхность образована n треугольниками. Это означает, что достаточно для каждого из них вычислить площадь, а затем сложить полученные значения и результатом будет искомый показатель. Тем не менее, сделать это не всегда просто для пирамиды произвольного типа. Приведем пример. Ниже рисунок демонстрирует три пирамиды, которые называются четырехугольными наклонными.

С первого взгляда видно, что все боковые треугольники являются разными. Это означает, что для определения их площадей необходимо знать все стороны основания и высоту каждого треугольника. Она называется «апофемой». Если апофему i-го треугольника обозначить символом hi, а длину соответствующей стороны основания назвать ai, тогда получим для общего типа пирамиды формулу боковой поверхности площади:

Таким образом, для вычисления величины S фигуры произвольного типа необходимо знать 2*n ее параметров.

Правильные пирамиды и их боковая поверхность

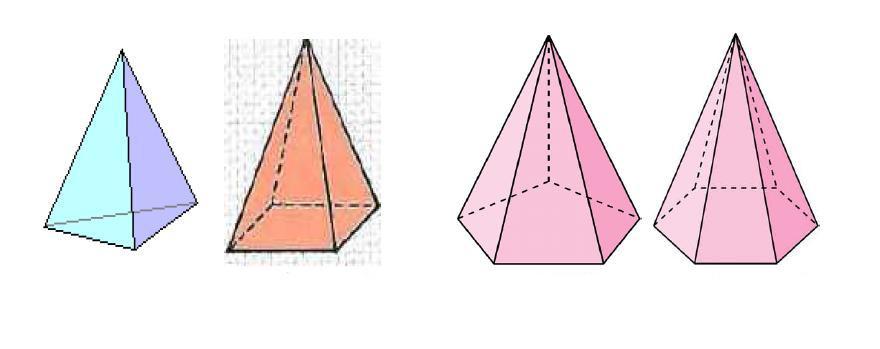
Приведенная в предыдущем пункте формула площади поверхности пирамиды общего типа принимает конкретный вид для правильных фигур. Правильной называется та пирамида, которая содержит в основании равностороннюю и равноугольную фигуру, а ее высота попадает точно в центр основания. На рисунке ниже показан набор правильных пирамид, изготовленных из бумаги:

Важно не путать величину h1 в формуле с высотой h пирамиды. Апофема h1 и высота h связаны единым равенством через длину основания для любой правильной пирамиды.

Задача на вычисление боковой поверхности треугольной пирамиды

Известно, что треугольная правильная пирамида имеет высоту 43 см и длину основания 12 см. Чему равна площадь ее боковой поверхности?

Рассмотрев прямоугольный треугольник внутри этой пирамиды, который образован сторонами h1, h и 1/3 высоты основания, получаем:

h1 = √(h2 + a2/12) = √(432+122/12) = 43,14 см.

Теперь осталось применить записанную выше формулу для S, учитывая при этом, что n=3. Получаем:

S = 1/2*n*a*h1 = 1/2*3*12*43,14 = 776,52 см2.

Записанная формула определения апофемы через высоту справедлива только для треугольной правильной пирамиды.

Источник

Нахождение площади правильной пирамиды: формулы

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.

Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.

Формула площади правильной пирамиды

1. Общая формула

Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.

Боковой гранью правильной пирамиды является равнобедренный треугольник.

Площадь треугольника вычисляется по формулам:

1. Через длину основания (a) и высоту (h):

2. Через основание (a) и боковую сторону (b):

Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.

2. Площадь правильной треугольной пирамиды

Основание: равносторонний треугольник.

Источник

Площадь боковой поверхности разных пирамид

Перед изучением вопросов о данной геометрической фигуре и её свойствах, следует разобраться в некоторых терминах. Когда человек слышит о пирамиде, ему представляются большущие постройки в Египте. Так выглядят самые простые из них. Но они бывают разных видов и форм, а значит и формула вычисления для геометрических фигур будет разной.

Виды фигуры

Пирамида – геометрическая фигура, обозначающая и представляющая собой несколько граней. По сути – это тот же многогранник, в основании которого лежит многоугольник, а по бокам расположены треугольники, соединяющиеся в одной точке – вершине. Фигура бывает двух основных видов:

В первом случае, в основании лежит правильный многоугольник. Тут все боковые поверхности равны между собой и сама фигура порадует глаз перфекциониста.

Термины и обозначения

Формулы площади

Находить площадь боковой поверхности пирамиды любого типа можно несколькими способами. Если фигура не симметричная и представляет собой многоугольник с разными сторонами, то в данном случае легче вычислить общую площадь поверхности через совокупность всех поверхностей. Иными словами – надо посчитать площадь каждой грани и сложить их вместе.

В зависимости от того, какие параметры известны, могут потребоваться формулы вычисления квадрата, трапеции, произвольного четырёхугольника и т.д. Сами формулы в разных случаях тоже будут иметь отличия.

В случае с правильной фигурой находить площадь намного проще. Достаточно знать всего несколько ключевых параметров. В большинстве случаев требуются вычисления именно для таких фигур. Поэтому далее будут приведены соответствующие формулы. В противном случае пришлось бы расписать всё на несколько страниц, что только запутает и собьёт с толку.

Основная формула для вычисления площади боковой поверхности правильной пирамиды будет иметь следующий вид:

S=½ Pa ( P – периметр основания, а – апофема)

Рассмотрим один из примеров. Многогранник имеет основание с отрезками A1, А2, А3, А4, А5, и все они равны 10 см. Апофема пусть будет равна 5 см. Для начала надо найти периметр. Так как все пять граней основания одинаковые, можно находить так: Р=5*10=50 см. Далее применяем основную формулу: S =½*50*5=125 см в квадрате.

Площадь боковой поверхности правильной треугольной пирамиды вычислить легче всего. Формула имеет следующий вид:

S =½* ab *3, где а – апофема, b – грань основания. Множитель тройки здесь означает количество граней основания, а первая часть – площадь боковой поверхности. Рассмотрим пример. Дана фигура с апофемой 5 см и гранью основания 8 см. Вычисляем: S =1/2*5*8*3=60 см в квадрате.

Тут для начала следует найти периметры оснований: р_01 =3*4=12 см; р_02=6*4=24 см. Осталось подставить значения в основную формулу и получим: S =1/2*(12+24)*4=0,5*36*4=72 см в квадрате.

Таким образом, можно найти площадь боковой поверхности правильной пирамиды любой сложности. Следует быть внимательным и не путать эти вычисления с полной площадью всего многогранника. А если это всё же понадобится сделать – достаточно вычислить площадь самого большого основания многогранника и прибавить её к площади боковой поверхности многогранника.

Видео

Закрепить информацию о том, как найти площадь боковой поверхности разных пирамид, вам поможет это видео.

Источник

Как найти площадь боковой поверхности пирамиды: формулы, пример задачи

В школьном курсе стереометрии изучают свойства разных пространственных фигур. Одной из них является пирамида. Данная статья посвящена вопросу о том, как найти у пирамиды площадь боковой поверхности. Также раскрывается вопрос определения этой площади для усеченной пирамиды.

Что такое пирамида?

Многие, услышав слово «пирамида», сразу представляют грандиозные сооружения Древнего Египта. Действительно, гробницы Хеопса и Хефрена являются правильными четырехугольными пирамидами. Тем не менее пирамидой также является тетраэдр, фигуры с пяти-, шести-, n-угольным основанием.

Вам будет интересно: Passive Voice: упражнения с ответами, таблица

Точка, с которой соединены все вершины углов основания, не лежит в его плоскости. Она называется вершиной пирамиды. Если из нее провести к основанию перпендикуляр, то мы получим высоту. Фигура, в которой высота пересекает основание в геометрическом центре, получила название прямой. Иногда прямая пирамида имеет правильное основание, например квадрат, равносторонний треугольник и так далее. В этом случае она называется правильной.

При вычислении у пирамиды площади боковой поверхности удобно работать с правильными фигурами.

Площадь поверхности боковой фигуры

Как найти у пирамиды площадь боковой поверхности? Можно понять это, если ввести соответствующее определение и рассмотреть развертку на плоскости для этой фигуры.

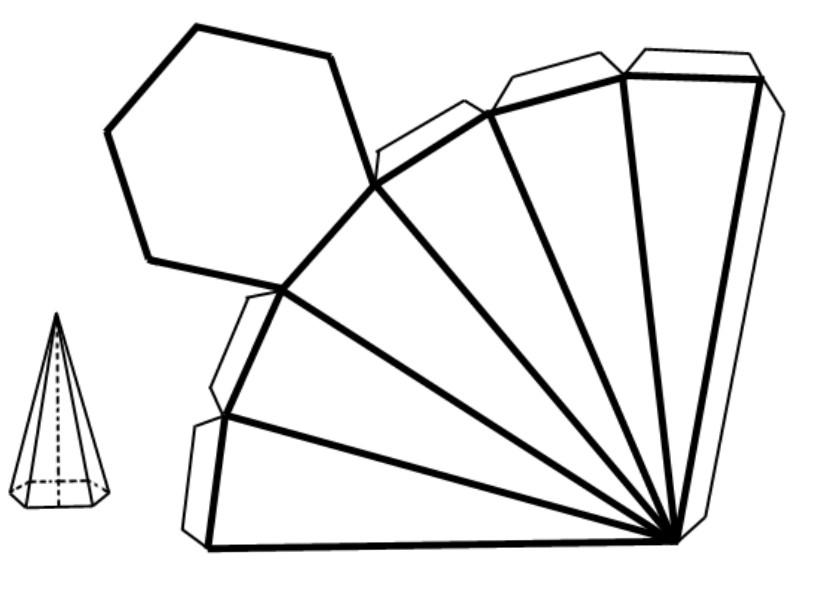
Если вдоль бокового ребра разрезать поверхность и развернуть ее на плоскости, то получится развертка пирамиды. Для примера ниже показана развертка шестиугольной пирамиды.

Видно, что боковая поверхность образована шестью одинаковыми треугольниками.

Теперь не трудно догадаться, как у пирамиды найти площадь боковой поверхности. Для этого следует сложить площади всех треугольников. В случае n-угольной правильной пирамиды, сторона основания которой равна a, для рассматриваемой поверхности можно записать формулу:

Усеченная пирамида и ее поверхность

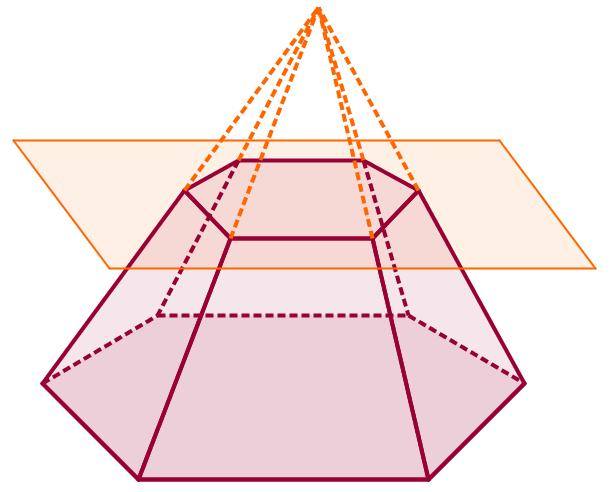
Как можно догадаться из названия, усеченную пирамиду можно получить из обычной фигуры. Для этого нужно отсечь плоскостью, параллельной основанию, вершину. Ниже рисунок демонстрирует этот процесс для шестиугольной фигуры.

Ее боковая поверхность представляет собой сумму площадей одинаковых равнобедренных трапеций. Формула для площади боковой поверхности усеченной пирамиды (правильной) имеет вид:

Расчет боковой поверхности для треугольной пирамиды

Покажем, как найти площадь боковой поверхности пирамиды. Допустим, у нас правильная треугольная, разберемся на примере конкретной задачи. Известно, что сторона основания, представляющего собой равносторонний треугольник, равна 10 см. Высота фигуры равна 15 см.

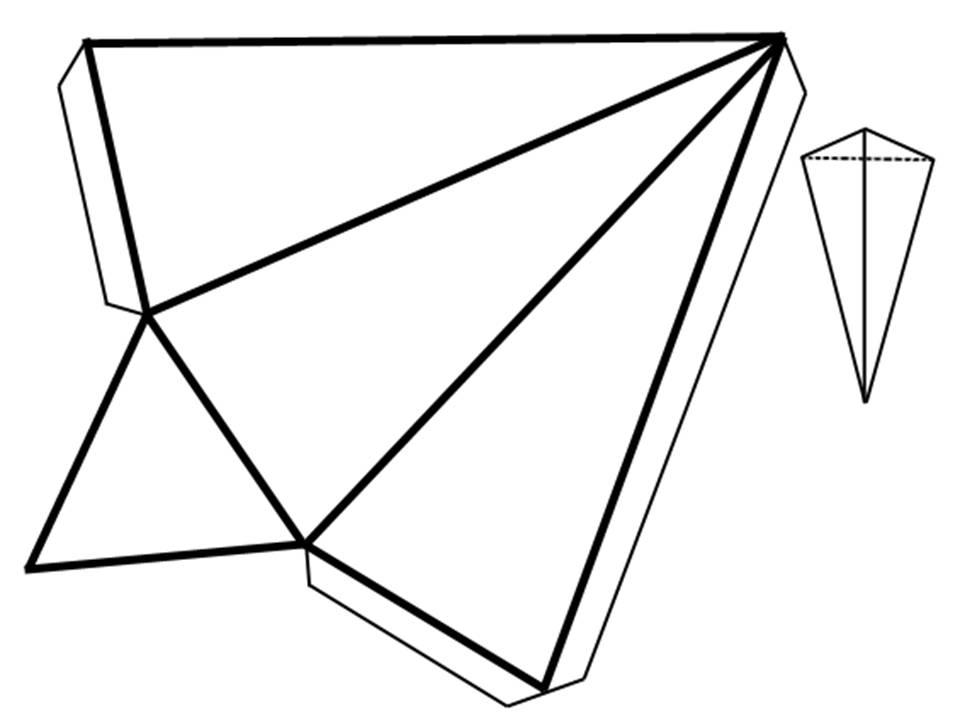
Развертка этой пирамиды показана на рисунке. Чтобы воспользоваться формулой для Sb, необходимо сначала найти апофему hb. Рассматривая прямоугольный треугольник внутри пирамиды, построенный на сторонах hb и h, равенство можно записать следующее:

Подставляем данные и получаем, что hb≈15,275 см.

Теперь можно воспользоваться формулой для Sb:

Sb = n*a*hb/2 = 3*10*15,275/2 = 229,125 см2

Заметим, что основание треугольной пирамиды, как и ее боковая грань, образовано треугольником. Тем не менее этот треугольник при вычислении площади Sb не учитывается.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Перечень вопросов, рассматриваемых в теме:

Пирамида – многогранник, составленный из n-угольника и n треугольников

Основание пирамиды – грань пирамиды, являющаяся n-угольником

Вершина пирамиды – общая точка всех треугольников, лежащих в боковых гранях.

Боковая грань – грань пирамиды, являющаяся треугольником

Боковые ребра – общие отрезки боковых граней

Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание

Апофема – высота боковой грани правильной пирамиды

Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а отрезок, соединяющий вершину и центр основания пирамиды, является высотой

Усеченная пирамида – многогранник, образованный двумя n-угольниками, расположенными в параллельных плоскостях (нижнее и верхнее основание) и n-четырехугольников (боковые грани).

Площадь полной поверхности пирамиды – сумма площадей всех граней пирамиды

Площадь боковой поверхности пирамиды – сумма площадей боковых граней пирамиды

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. и профильным изучением математики общеобразоват. Учреждений.. – М.: Дрофа, 2009. – 368 с.: ил. (117 с. – 121 с.)

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255 с. (65 с. – 68 с.)

Открытые электронные ресурсы:

Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/

Теоретический материал для самостоятельного изучения

Рассмотрим многоугольник A₁A₂. A_n и точку Р, не лежащую в плоскости этого многоугольника (рис.1). Соединив точку Р с вершинами многоугольника, получим n треугольников: PA₁A₂, PA₂A₃,…, PA_nA₁.

Многогранник, составленный из n-угольника A₁A₂. A_n и n треугольников, называется пирамидой. Многоугольник A₁A₂. A_n называется основанием, а треугольники PA₁A₂, PA₂A₃,…, PA_nA₁ – боковые грани пирамиды, отрезки PA₁, PA₂,…, PA_n – боковые ребра пирамиды, точка Р – вершина пирамиды. Пирамиду с основанием A₁A₂. A_n и вершиной Р называют n-угольной пирамидой и обозначают PA₁A₂. A_n.

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 3) или быть одним из боковых ребер (рис. 4).

Рисунок 3 – высота вне пирамиды

Будем называть пирамиду правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности (рис.5).

Рисунок 5 – Правильная пирамида

Правильная пирамида обладает несколькими хорошими свойствами. Давайте выясним, какими.

Рассмотрим правильную пирамиду PA₁A₂. A_n (рис. 5).

Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А₁О, А₂О. А_nО.

Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.

Таким образом, верны следующие утверждения:

Введем еще одно определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рисунке 5 PE – одна из апофем.

Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.

Возьмем произвольную пирамиду PA₁A₂. A_n и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В₁,В₂. В_n (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A₁A₂. A_n и В₁В₂. В_n (нижнее и верхнее основания соответственно), расположенные в параллельных плоскостях и n четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂, … A₁A_nB_nB₁ (боковые грани), называется усеченной пирамидой.

Рисунок 6 – Усеченная пирамида

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды. На рисунке 7 отрезки HH₁ и В1O –высоты усеченной пирамиды.

Рисунок 7 – Высота усеченной пирамиды

Площадь поверхности пирамиды

Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.

Для пирамиды, верно равенство S_полн= S_бок+S_осн.

Докажем теорему для площади боковой поверхности правильной пирамиды.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Для площади боковой поверхности усеченной пирамиды верна следующая теорема

Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Примеры и разбор решения заданий тренировочного модуля

Задание 1. В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?

Поскольку в пирамиде все боковые грани равны, то и площади их будут равны. Знаем, что площадь боковой грани на 15 меньше площади основания, значит она равна 27. В пятиугольной пирамиде боковых граней 5. Таким образом площадь полной поверхности равна 27*5+42 = 177.

Задание 2. В правильной пирамиде высота боковой грани равна 10, а в основании лежит квадрат со стороной 4. Чему равна площадь боковой поверхности?

Боковая грань пирамиды – это треугольник. Все боковые грани этой пирамиды равны между собой, так как пирамида правильная. Вычислим площадь треугольника: ½*4*10=20. В основании пирамиды лежит квадрат, значит боковых граней будет 4. Таким образом, площадь боковой поверхности равна 4* 20=80.

Источник