Что такое площадь фигуры 3 класс
Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
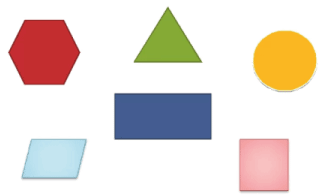
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
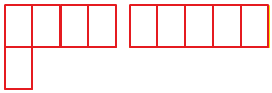
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
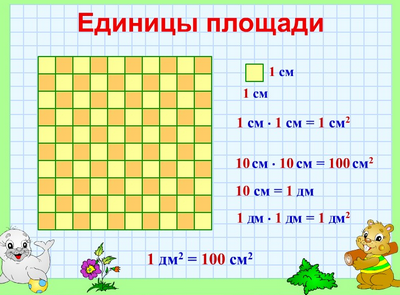
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
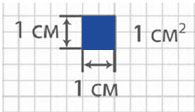
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
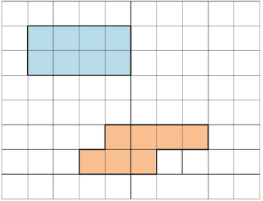
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
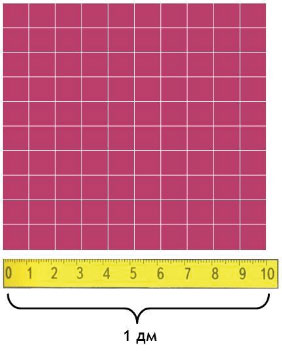
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
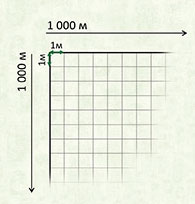
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
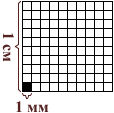
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
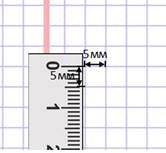
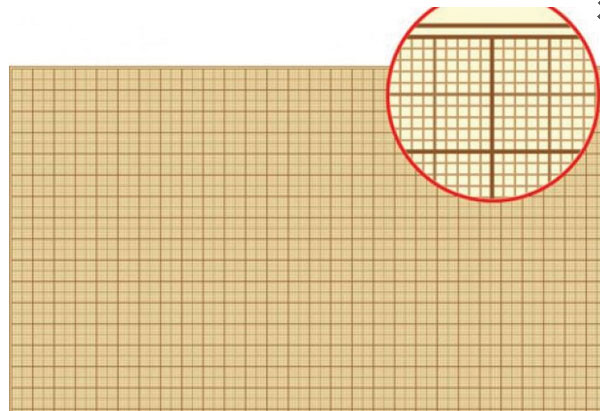
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Слово «ар» при числах сокращённо записывают так:
Гектар
Слово «гектар» при числах сокращённо записывают так:
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Поделись с друзьями в социальных сетях:
Урок математики в 3-м классе по теме: «Площадь. Единицы площади»
1. Дать представление о площади фигур, познакомить с различными способами сравнения фигур: “на глаз”, путём наложения одной фигуры на другую, с использованием различных единиц измерения площадей.
2. Закрепить знание свойств геометрических фигур.
3. Закрепить умение точно производить измерения и чертить квадрат и прямоугольник.
4. Закрепить знание изученных таблиц умножения и соответствующих случаев деления.
5. Развивать логическое мышление и пространственное воображение.
6. Воспитывать аккуратность при выполнении работы.
Оборудование. Для учащихся: геометрические фигуры, линейка, простой карандаш, цветные карандаши, рабочая тетрадь, листы с заданиями.
Для учителя: геометрические фигуры, карточка со словом “Площадь “, задания № 2 и №3 в увеличенном виде.
Начинаем наш урок.
Надеюсь, он пойдёт вам впрок.
Постарайтесь всё понять,
Ответы полные давать.
II. Запись в тетради числа и слов “Классная работа”.
III. Устный счёт и чистописание.
а) Найдите в каждом ряду числа, которые не являются результатом табличного умножения.
Запишите числа 17, 41, 11, 7, 71. Обратите внимание на образцы написания цифр.
Докажите, что оставшиеся числа являются результатом табличного умножения.
б) Из данных чисел выбери пары, произведения и частные которых равны 6.
1 4 6 2 54 12 3 36 7 8 24 18 42 48 9
в) Сторона квадрата 2 см. Чему равен периметр? Найди правильное решение.
Дайте общее название фигурам.
IV. Сообщение темы урока.
Знание таблиц умножения и соответствующих случаев деления, свойств геометрических фигур понадобятся нам при изучении темы: Площадь. Единицы площади.
Сегодня мы выясним, что такое площадь фигуры и как можно сравнить площади фигур.
На доску вывешивается табличка: Площадь
V. Работа по теме урока.
1. Словарная работа.
Назовите орфограммы в слове “ Площадь”.
2. Работа с геометрическим материалом.
а) Возьмите зелёный и белый квадраты. Покажите квадрат, который больше.
Про такие фигуры говорят, что площадь зелёного квадрата больше площади белого квадрата.
Как ещё можно сравнить площади этих фигур?
Можно наложить одну на другую.
Наложите и сравните площади квадратов.
Белый квадрат полностью вместился в зелёном, значит площадь зелёного квадрата больше площади белого квадрата.
б) Возьмите жёлтый и красный круги. Сравните площади и покажите круг, площадь которого меньше.
Площади кругов равны, так как при наложении круги полностью совпали.
Что же такое площадь фигуры? Как вы думаете?
Если правильного ответа не будет, учитель сообщает:
Площадь-это место, которое занимает фигура на плоскости.
Как мы сравнивали площади фигур?
“На глаз” и наложением друг на друга.
Встаньте дружно из-за парт
И скорее стройтесь в ряд!
Повернитесь вправо, влево,
Наконец, присядьте смело!
Поработаем ногами,
Раз, два, три!
Поработаем руками!
Раз, два, три!
Улыбнёмся: день хороший,
И похлопаем в ладоши.
3. Продолжение работы с геометрическим материалом.
а) Возьмите фиолетовый прямоугольник и белый квадрат.
Как удобнее сравнивать площади прямоугольника и квадрата “на глаз” или наложением?
Дети пытаются сравнить площади фигур “на глаз” и наложением.
“На глаз” или наложением сравнить площади прямоугольника и квадрата нельзя, фигуры разные по форме и ни одна полностью не вмещается в другой.
Как же сравнить площади этих фигур?
Если правильного ответа не будет, учитель сам предлагает начертить прямоугольник и квадрат в тетради.
а) Назовите общие свойства прямоугольника и квадрата.
б). Вычерчивание прямоугольника и квадрата в тетради.
Измерьте сторону квадрата.
Начертите квадрат. Укажите на чертеже длину стороны квадрата.
Измерьте длину и ширинку прямоугольника.
Начертите прямоугольник. Укажите длины сторон прямоугольника.
Как же сравнить площади этих фигур?
1. Если правильного ответа не будет, обратить внимание детей на то, что, начертив фигуры в тетради, мы разбили их на одинаковые фигуры меньшего размера – клетки тетради.
Можно посчитать клетки.
Сравните площади квадрата и прямоугольника.
Площадь квадрата больше площади прямоугольника.
Большую площадь имеет та фигура, которая содержит большее число клеток.
2. Но площадь фигур можно измерить и другими мерками. Можно разбить фигуру на одинаковые треугольники или большие квадраты.
Демонстрация прямоугольника разбитого на одинаковые треугольники.
3. Разобьём квадрат и прямоугольник на квадраты со стороной 1см. Подсчитайте, сколько квадратов со стороной 1см поместилось в квадрате? В прямоугольнике? Запишите числа и сравните их.
Сравните площади фигур.
Площадь квадрата больше площади прямоугольника.
Результат сравнения площадей не зависит от выбора единиц измерения.
4. Как удобнее подсчитать квадраты, на которые разбит прямоугольник?
3 ряда по 5 квадратов, 5 • 3 = 15
5 столбцов по 3 квадрата, 3 • 5 = 15
5. Подведём итог наших наблюдений.
Что же такое площадь фигуры?
Как можно сравнить площади фигур?
Как же долго мы сидели,
Наши руки онемели,
Наши ноги затекли,
Ими топнем: раз, два, три!
1. Как легче узнать, площадь, какой фигуры больше?
Учебник “Математика” 3 класс. Авторы: М. И. Моро, М. А. Бантова и др. 2002 год.
Страница 69, задание на смекалку.
2. Раздели на три фигуры одинаковые по площади, и раскрась разными карандашами.
Построй фигуру равную по площади данной, но другой формы.
3. Задание на развитие пространственного воображения.
Раскрась фигуру. Существует два варианта: а) прямоугольник сверху, а квадрат снизу, б) прямоугольник снизу, а квадрат сверху. Выберите любой вариант.
Площадь фигуры 3 класс
Описание презентации по отдельным слайдам:
Описание слайда:
ПЛОЩАДЬ.
ЕДИНИЦЫ ПЛОЩАДИ.
Работу выполнила:
Проскурина Ольга Геннадьевна,
учитель начальных классов
МБОУ «Школа N18»
г. Нижнего Новгорода
Описание слайда:
Организационный момент
На уроке наши глаза внимательно
Смотрят и все … (видят).
Уши внимательно слушают
И всё …(слышат).
Голова хорошо … (думает0.
Описание слайда:
26 октября.
Классная работа..
Описание слайда:
5 ∙ 2 = 10 14 : 2 = 7
9 ∙ 1 = 9 16 : 8 = 2
4 ∙ 5 = 20 25 : 5 = 5
Найди число
Какие числа закрыты
Описание слайда:
Сколько будет, если взять 3 раза по 4?
Сколько будет: 6 троек?
Сколько раз по 5 входит в число 10?
3 умножить на 4.
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Главная площадь нашей страны
Описание слайда:
Владимир Даль
это величина, которая указывает, сколько места занимает фигура на плоскости.
Описание слайда:
Описание слайда:
Способы измерения площади…
?
Описание слайда:
Описание слайда:
РАБОТА С
ГЕОМЕТРИЧЕСКИМ
МАТЕРИАЛОМ
КАК МОЖНО СРАВНИТЬ ЭТИ ФИГУРЫ?
Они имеют РАВНЫЕ
ПЛОЩАДИ
Описание слайда:
СРАВНИТЕ ФИГУРЫ
Что можно сказать про площадь треугольника?
ПЛОЩАДЬ
треугольника меньше ПЛОЩАДИ
квадрата
Описание слайда:
СРАВНИТЕ ФИГУРЫ
Можно ли на «глаз» или наложением определить, площадь какой фигуры больше?
20
18
Площадь больше
Площадь меньше
Описание слайда:
СПРАВКА
При разных мерках получается разный результат измерения.
Поэтому сравнивать, складывать и вычитать величины можно только тогда, когда они выражены одинаковыми мерками.
Описание слайда:
Описание слайда:
Описание слайда:
Работа по учебнику
Описание слайда:
НАЧЕРТИ
ПРЯМОУГОЛЬНИК СО СТОРОНАМИ
3 СМ И 5 СМ
ПОСЧИТАЙ СКОЛЬКО КЛЕТОЧЕК В НЕМ ПОМЕСТИЛОСЬ.
Описание слайда:
Описание слайда:
3 + 3 + 3 + 3 = 12
11 + 11 + 11 + 11 = 44
8 + 8 + 8 + 8 = 32
Описание слайда:
В качестве общепринятой единицы измерения площадей (мерок) используют
квадрат со стороной 1 см.
Это измерение называют:
квадратный сантиметр – 1 см².
Описание слайда:
Какие единицы измерения площади вы знаете?
Что значит квадратный сантиметр?
1 см 2
Найдите площади данных фигур.
2.
1.
3.
Описание слайда:
Это прямоугольник со сторонами 6 см и 4 см.
Разделим его на квадратные сантиметры
Ширина прямоугольника
Длина прямоугольника
Сколько полос с квадратами получилось?
Сколько квадратов в каждой полосе?
Как узнать, сколько всего квадратов?
Что такое 6?
Что такое 4?
Сделайте вывод, как найти площадь прямоугольника?
4
6
S = a · b
a
b
а-длина, b-ширина
Описание слайда:
Описание слайда:
Площадь прямоугольника
1.Чтобы найти площадь прямоугольника, измеряют его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел.
2.Чтобы найти площадь прямоугольника, надо его длину умножить на ширину.
Описание слайда:
Найдите площадь прямоугольника
4 см
6 см
S=a•b
S = 6 • 4 = 24 см²
Описание слайда:
Электронная физминутка для глаз «Крошка Енот»
Описание слайда:
Описание слайда:
Работа по учебнику
Описание слайда:
Описание слайда:
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Деление с остатком 3 класс
Памятки по математике 3 класс
Рабочая программа внеурочной деятельности по математике в 5 классе «Математическая шкатулка»
Конспект урока по математике для 2 класса на тему «Сложение и вычитание в пределах 100. Закрепление».
Урок на тему «Координаты»
Урок по теме «Деление обыкновенных дробей» 6 класс
Самостоятельная работа на тему «Элементарная теория делимости» (5 класс)
Презентация к уроку математики в малокомплектной школе 1,3 класс
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5429166 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»
Время чтения: 1 минута
Чем заняться с детьми в новогодние праздники в Москве
Время чтения: 4 минуты
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Как найти площадь прямоугольника 3 класс
Названия геометрических фигур происходят от количества их сторон. Например, треугольник, четырехугольник, пятиугольник. Но есть фигуры, которые названы по другим признакам, например, прямоугольник, квадрат, ромб, трапеция. Все эти фигуры — четырехугольники, но отличаются друг от друга величиной углов и сторон.
Квадрат — прямоугольник, у которого все углы по 90 градусов и стороны равные.
Такие отличия есть и у других фигур, например, треугольники подразделяются на прямоугольные, равносторонние, равнобедренные и разносторонние. Свойства фигуры зависят как от количества сторон, так и от других характеристик — величины углов и сторон. Только измерив все параметры, можно точно описать фигуру и определить, какими формулами и правилами пользоваться при вычислениях.
Под этим термином понимают часть плоскости, ограниченной несколькими замкнутыми (соединенными) линиями. В результате соединения линий образуется отрезки, которые называются сторонами фигуры и точки соприкосновения, которые носят название вершин. У треугольника три стороны и три вершины, у четырехугольника — четыре стороны и четыре вершины.
В геометрии есть фигуры, которые выпадают из этого ряда. Это точка, прямая линия, отрезок, луч. Отличаются они от остальных фигур, тем, что не занимают никакой площади, это просто части линии.
Что такое площадь
Теперь рассмотрим еще одно понятие геометрии — площадь. Это часть плоскости, которая находится внутри многоугольника. Другими словами, все, что находится между сторонами фигуры и является ее площадью. Геометрия — часть математики, то есть, наука точная, которая стремится все измерить и описать цифрами. Не стала исключением и площадь. Часть плоскости, которая находится внутри фигуры, разбили на маленькие части с равными сторонами, идущими под прямым углом друг к другу. Такая фигура называется квадрат.
Квадрат — геометрическая фигура из четырех равных сторон и четырех прямых углов.
Расчет площади прямоугольника
Разберем простую задачу — как высчитать площадь прямоугольника? Можно решить ее двумя способами. Самый простой, но самый длинный и трудоемкий — нарисовать прямоугольник и с помощью карандаша и линейки разбить его на маленькие квадратики. Затем посчитать количество квадратиков и узнать, сколько их поместилось внутри.
Такой способ простой и доступный, если длина сторон прямоугольника — целое количество сантиметров или метров. А вот при их нецелом количестве, например стороны три с половиной и четыре с половиной сантиметра (3,5 см и 4,5 см), посчитать сложнее. Еще сложнее, если стороны, например 3см и 2 мм и 4 см и 7 мм. Рисовать придется миллиметровые квадратики, что довольно сложно и долго.
Ученые древности, идя таким путем заметили интересную особенность, если посчитать квадраты внутри фигуры и сравнить их с результатом умножения длин сторон прямоугольника, то они окажутся одинаковыми. Проверив это на многих прямоугольниках и квадратах составили правило:
Площадь прямоугольника равна длине умноженной на ширину.
В учебниках можно найти и другую формулировку — площадь прямоугольника равна произведению соседних сторон, или еще иначе — площадь прямоугольника равна произведению основания на высоту. Суть этих утверждений одна и та же. Выражается она в формуле:
S=AB ∙BC.
Использование этой формулы — самый простой способ, как вычислить площадь прямоугольника с разными сторонами. Подходит он и для решения задачи вычисления квадрата (прямоугольника с равными сторонами). Для квадрата формула может выглядеть несколько иначе.
S=АВ 2
Периметр
Еще одна важная характеристика прямоугольника — периметр. Это сумма длин всех сторон. Периметр легко найти, измерив все стороны и сложив результаты. Но, как и в случае с площадью, лучше воспользоваться формулой. Сначала найдем периметр квадрата:
Р = АВ+ВС+СD+AD.
Но у квадрата все стороны одинаковые, значит, выражение можно записать иначе:
Р= АВ+АВ=АВ=АВ = 4 ∙ АВ, или 4АВ.
Для прямоугольника с разными сторонами периметр находится по такой же формуле:
Р = АВ+ВС+СD+AD.
Но здесь равны не все стороны, а только противоположные:
АВ= СD и ВС= AD
Перепишем начальную формулу по-другому:
Р= (АВ +СD) и (ВС + AD). Из равенства сторон получим Р=2АВ+2ВС + 2(АВ+ВС). Словами это будет звучать так:
Периметр прямоугольника равен сумме соседних сторон умноженной на два.
Как видно из приведенных утверждений, площадь и периметр прямоугольника можно вычислить двумя способами — непосредственным измерением и вычислением. Второй способ намного удобнее, особенно, если приходится находить площади и периметры реальных участков, например, площадки под строительство, дачного участка, комнаты.
Смотрите также другие геометрические фигуры: