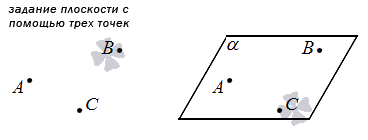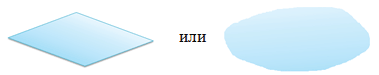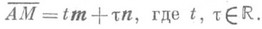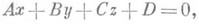Что такое плоскость геометрия
Плоскость

Всего получено оценок: 107.
Всего получено оценок: 107.
Плоскость – это основная единица планиметрии. Для правильного восприятия сложных фигур, таких как, пирамида, конус или призма, необходимо понимать и, главное, представлять себе, что такое плоскость.
Определение плоскости
Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.
Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.
Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.
Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.
Способы задания плоскостей
Плоскость может быть задана тремя точками, нележащими на одной прямой. Из этого утверждения следуют еще два варианта задания плоскостей. При этом специального знака плоскостей не существует.
Плоскость можно задать двумя пересекающимися прямыми, тогда одной точкой будет служить точка пересечения прямых, а двумя другими произвольные точки на одной и второй прямой.
Еще один вид это задание прямой и точкой, нележащей на этой прямой. По аналогии со вторым вариантам: одна точка уже есть и не лежит на прямой, а две других это произвольные точки имеющейся линии.
Взаимное расположение прямой и плоскости
Прямая в пространстве может быть параллельной плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.
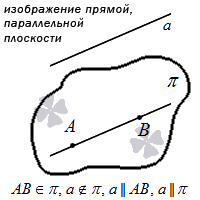
Прямая параллельная плоскости, если она не имеет общих точек с ней. Признак параллельности прямой и плоскости крайне прост: прямая параллельна плоскости, если параллельна любой прямой лежащей в этой плоскости.
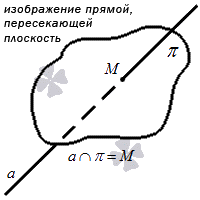
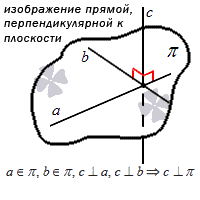
Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, необходимо провести прямую в плоскости через точку пересечения. Тогда угол между этими прямыми и будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Признак перпендикулярности прямой и плоскости звучит так: прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоскости и пересекает плоскость в месте пересечения этих прямых.
Прямая в пространстве может лежать в плоскости, если две любые точки этой прямой принадлежат этой плоскости.
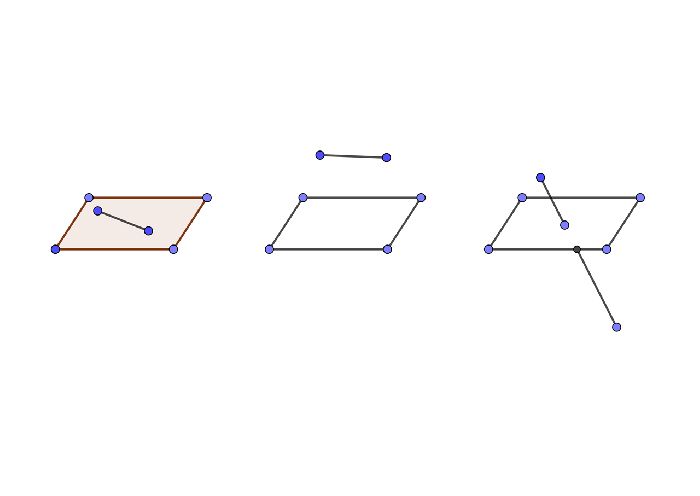
Взаимное расположение плоскостей
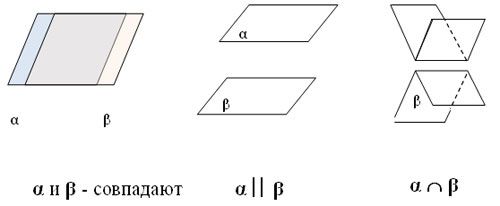
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.
Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.
Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.
Что мы узнали?
Мы дали определение и привели примеры плоскости. Выделили варианты пересечения прямой и плоскости и пересечения плоскостей. Привели несколько признаков, относящихся с плоскостям и разобрали все случаи существования плоскостей в пространстве.
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
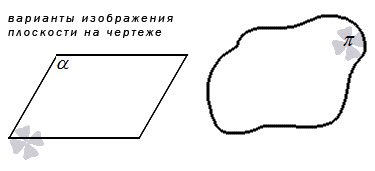
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
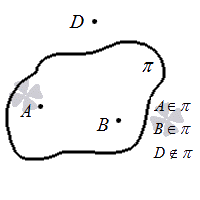
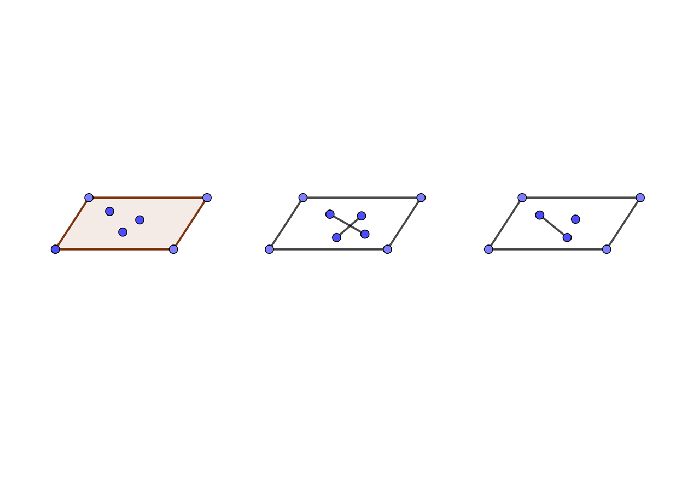
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
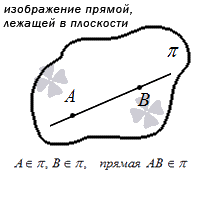
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Графически этот вариант расположения выглядит так:
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
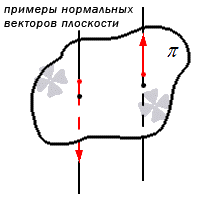
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
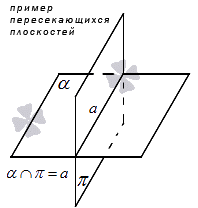
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
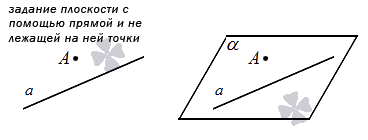
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
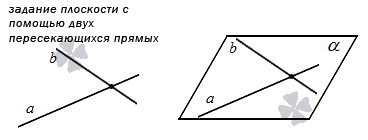
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
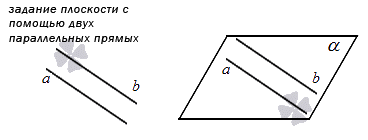
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
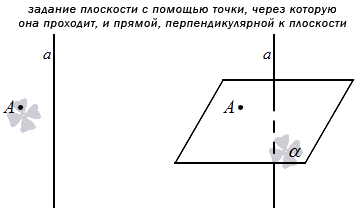
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
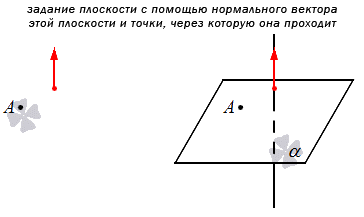
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.
Плоскость
Понятие плоскости
поверхность школьной доски:
Эти поверхности ограничены, у них есть края. Но представление о плоскости мы имеем с их помощью.
Только плоскость простирается безгранично (в любом направлении, заданном на этой плоскости).
Понятие плоскость принадлежит к числу основных понятий геометрии.
Обозначение плоскости
Конечно, нарисовать плоскость, у которой нет краев, невозможно. Поэтому, при изображении плоскости, рисуют только ее часть:
Обозначается плоскость строчными буквами греческого алфавита – α (альфа), β (бета), γ (гамма) и т.д.:
Буквы пишут либо рядом с плоскостью, либо на плоскости.
Определение плоскости
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки. ( то есть, любая прямая, соединяющая две ее точки, целиком принадлежит ей).
Поделись с друзьями в социальных сетях:
Плоскость в пространстве – необходимые сведения, способы задания плоскости, плоскости в пространстве
Определение плоскости
Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.
Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.
Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.
Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.
Обозначение плоскости
Конечно, нарисовать плоскость, у которой нет краев, невозможно. Поэтому, при изображении плоскости, рисуют только ее часть:
Обозначается плоскость строчными буквами греческого алфавита – α (альфа), β (бета), γ (гамма) и т.д.:
Буквы пишут либо рядом с плоскостью, либо на плоскости.
Взаимное расположение прямой и плоскости
Прямая в пространстве может быть параллельной плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.
Прямая параллельная плоскости, если она не имеет общих точек с ней. Признак параллельности прямой и плоскости крайне прост: прямая параллельна плоскости, если параллельна любой прямой лежащей в этой плоскости.
Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, необходимо провести прямую в плоскости через точку пересечения. Тогда угол между этими прямыми и будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Признак перпендикулярности прямой и плоскости звучит так: прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоскости и пересекает плоскость в месте пересечения этих прямых.
Прямая в пространстве может лежать в плоскости, если две любые точки этой прямой принадлежат этой плоскости.
Рис. 2. Взаимное расположение прямой и плоскости.
Параллельные плоскости
Теперь рассмотрим подробнее каждый из названных выше случаев. Предположим, что в общей форме заданы следующие две плоскости:
A1*x + B1*y + C1*z + D1 = 0;A2*x + B2*y + C2*z + D2 = 0.
Как понять, являются ли они параллельными? Сделать это очень просто. Достаточно вспомнить о нормальных векторах. Если две плоскости параллельны между собой, значит, их нормали также параллельны. Выпишем координаты нормальных векторов к указанным плоскостям. Имеем:
Достаточным условием параллельности n1¯ и n2¯ является возможность задания одного из них через другой. Математически это записывается так:
Где k — некоторое (в том числе отрицательное) число. Если одну нормаль невозможно выразить путем умножения координат другой на число, то такие плоскости не будут параллельными.
Частным случаем параллельности плоскостей является их полное совпадение друг с другом. Тогда должны выполняться такие условия:
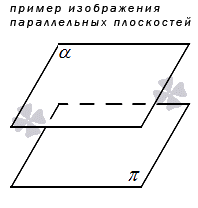
Пример параллельных плоскостей в пространстве приведен ниже.
Пересекающиеся плоскости и угол между ними
Поскольку существует всего два варианта взаимного расположения плоскостей, то достаточно проверить, являются ли они параллельными или нет. В случае их пересечения часто возникает необходимость в определении соответствующего угла. Согласно определению, углом между рассматриваемыми геометрическими объектами является угол между их нормалями.
Таким образом, изучая вопрос взаимного расположения плоскостей и угла между плоскостями, достаточно рассчитать скалярное произведение векторов n1¯ и n2¯. Соответствующая формула примет вид:
Угол между плоскостями θ всегда является острым, поскольку в числителе стоит модуль скалярного произведения.
Следует отметить частный случай, когда две плоскости пересекаются под углом 90o. Тогда достаточно вычислить скалярное произведение нормальных векторов. Оно будет равным нулю.
Взаимное расположение плоскостей
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.
Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.
Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.
Рис. 3. Расположение плоскостей.
Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Задана прямоугольная система координат Охуz в трехмерном пространстве. Координатные векторы i→, j→, k→ считаются нормальными векторами плоскостей Oyz, Oxz и Oxy. Это суждение верно, так как i→, j→, k→ ненулевые и расположены на координатных прямых Ox, Oy и Oz. Эти прямые перпендикулярны координатным плоскостям Oyz, Oxz и Oxy.
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат Охуz. Для определения нормального вектора n→=(A, B, C) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид Ax+By+Cz+D=0. То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Найти координаты нормального вектора, принадлежащего плоскости 2x-3y+7z-11=0.
Определить координаты направляющих векторов заданной плоскости x+2z-7=0.
По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x+2z-7=0 к виду 1·x+0·y+2z-7=0. Отсюда получим, что координаты нормального вектора данной плоскости равны (1, 0, 2). Тогда множество векторов будет иметь такую форму записи (t, 0, 2·t), t∈R, t≠0.
Ответ: (t, 0, 2·t), t∈R, t≠0.
При помощи уравнения плоскости в отрезках, имеющего вид xa+yb+zc=1, и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1a, 1b, 1c.
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
ПЛОСКОСТЬ
П. наз. метрической, если кроме отношения инцидентности определено расстояние между любой парой точек. Так, в Гильберта системе аксиом евклидовой геометрии расстояние вводится на базе аксиом конгруэнтности и непрерывности, и П. в этом случае наз. непрерывной (см. [1]). В случае невыполнения для П. аксиом непрерывности П. наз. дискретной (см., напр., Неархимедова геометрия), а П., состоящая из конечного числа точек, а следовательно, и прямых, наз. конечной (см. [7]).
Одним из путей изучения П. является введение в ней координат и тернарной операции с последующим ее изучением (см., напр., [7]), [8]).
В системе аксиом Вейля пространства Е 3 П. является производным понятием от понятий «вектор» и «точка». Под П., проходящей через точку 
В прямоугольной системе координат ( х, у, z).пространства Е 3 П. задается линейным уравнением
коэффициенты А, В, С определяют координаты нормального вектора этой П. В m-мерном пространстве re-мерные П. описываются системами линейных уравнений (см. [5]).
Взаимное расположение П. в различных m-мерных пространствах определяется соответствующими аксиомами инцидентности так же, как и свойства инцидентности плоскостей и прямых.
Лит.:[1] Гильберт Д., Основания геометрии, пер. с нем., М.- Л., 1948: [2] Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978; [3] Об основаниях геометрии, М., 1956; [4] Бахман Ф., Построение геометрии на основе понятия симметрии, пер. с нем., М., 1969; [5] Донеддю А., Евклидова планиметрия, пер. с франц., М., 1978; [6] Розенфельд Б. А., Многомерные пространства, М., 1966; [7] Dеmbоwski P., Finite geometries, В., 1968; [8] Pikеrt G., Projektive Ebenen, В., 1955. В. В. Афанасьев, Л. А. Сидоров.