Что такое плоскость общего положения

Плоскость общего положения

Плоскость общего положения образуется при движении прямой a по направляющим прямым m и n, когда они пересекаются или параллельны.

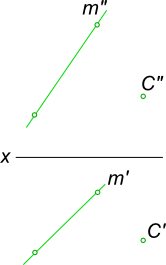
Поэтому, чтобы задать плоскость общего положения на эпюре Монжа достаточно указать: проекции трех различных точек, не принадлежащих одной прямой;

прямой и не принадлежащей ей точки;

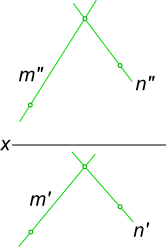
двух прямых, пересекающихся в собственной точке.

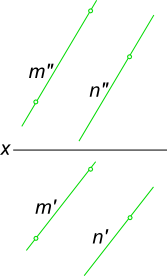
двух прямых, пересекающихся в несобственной точке.

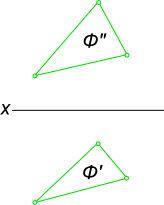
Плоскость может быть задана также проекциями отсека плоской фигуры Ф.

Данное утверждение может быть выражено иначе: три точки в пространстве не определяют положение плоскости проходящей через эти точки, только в том случае, если они принадлежат одной прямой.

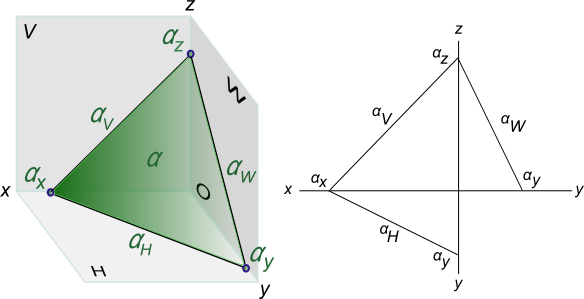
В некоторых случаях бывает целесообразным задавать плоскость общего положения прямыми, по которым эта плоскость пересекает плоскости проекции.

Такой вариант задания плоскости называют заданием плоскости следами.

Точки a_x, a_y, a_z в которых пересекаются (сходятся) два следа, называют точками схода следов.

Сопоставляя между собой пространственный чертеж и его плоскостную модель, мы видим, что задание плоскости следами обладает преимуществом перед другими вариантами ее задания: во-первых, сохраняется наглядность изображения, что позволяет легко представить положение плоскости в пространстве; во-вторых, при задании плоскости следами требуется указать только две прямые (в системе плоскостей проекций H и V) вместо четырех (параллельные прямые) или шести (треугольник).

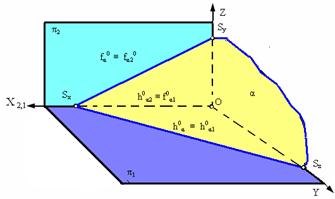
Показанная на рисунке плоскость общего положения α занимает общее (произвольное) положение по отношению к плоскостям проекций. Потому, что на эпюре Монжа следы плоскости общего положения составляют с координатными осями также произвольные углы.

Плоскость общего положения может занимать частное положение: Проецирующая плоскость; Плоскость уровня в результате применения методов преобразования ортогональных проекций: Метод преобразования.

Источник

Научная электронная библиотека

2.6. Общее и частные положения плоскости в пространстве

Плоскость общего положения

На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.

Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекций.

Плоскости, перпендикулярные плоскостям проекций
(проецирующие плоскости)

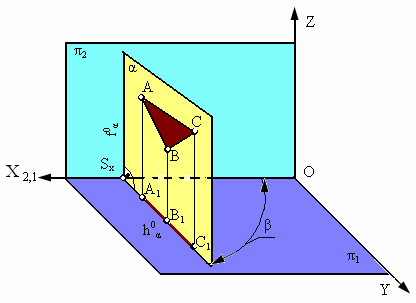
Плоскость α, перпендикулярная горизонтальной плоскости проекции π₁, называется горизонтально проецирующей (рис. 2.13).

Основным свойством горизонтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π₁ в прямую линию (горизонтальный след плоскости h 0 _α).

Угол b, который составляет горизонтальный след плоскости h 0 _a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций p₂. Фронтальный след такой плоскости перпендикулярен оси Х (f 0 _a ┴ X).

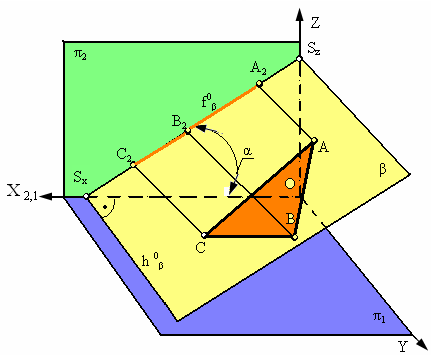
Плоскость b перпендикулярная фронтальной плоскости проекций π₂ называется фронтально проецирующей (рис. 2.14).

Рис. 2.12. Способы задания
плоскости:

Рис. 2.13. Горизонтально-проецирующая плоскость

Рис. 2.14. Фронтально-проецирующая плоскость

Основным свойством фронтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π₂ в прямую линию (фронтальный след плоскости f 0 _β). Угол a, который составляет фронтальный след плоскости f 0 _β с координатной осью Х, равен углу наклона плоскости b к плоскости проекций π₁. Горизонтальный след такой плоскости перпендикулярен оси Х.

Плоскости, параллельные плоскостям проекций

1. Горизонтальная плоскость γ || π₁.

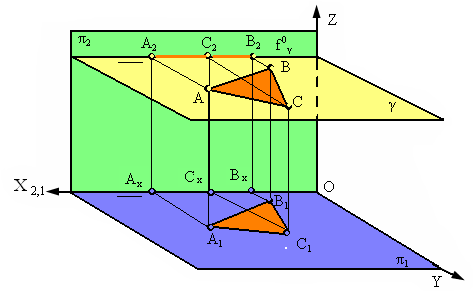
Плоскость γ, параллельная плоскости π₁, называется горизонтальной (рис. 2.15).

Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (Δ А₁В₁С₁ = ΔАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f_0g | | Х).

2. Фронтальная плоскость δ | | π₂.

Плоскость δ, параллельная плоскости π₂, называется фронтальной.

Рис. 2.15. Плоскость, параллельная горизонтальной плоскости проекций

Любая фигура, расположенная в такой плоскости, проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.

Горизонтальный след фронтальной плоскости параллелен оси Х.

Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.

Источник

Что такое плоскость общего положения

В зависимости от положения относительно плоскостей проекций различают плоскости общего положения и плоскости частного положения.

Плоскость общего положения – плоскость, наклоненная под произвольными углами к плоскостям проекций (рис.1).

Плоскости частного положения можно разделить на две группы – проецирующие плоскости и плоскости уровня. Плоскости частного положения чаще всего задаются следами.

Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня. Все объекты, лежащие в плоскости уровня, проецируются на параллельную плоскость проекций в натуральную величину.

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (рис.2).

Треугольник ABC, лежащий в горизонтальной плоскости уровня, проецируется на П1 в натуральную величину.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (рис. 3).

Треугольник ABC, лежащий во фронтальной плоскости уровня, проецируется на П2 в натуральную величину.

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (рис. 4).

Треугольник ABC, лежащий в профильной плоскости уровня, проецируется на плоскость П3 в натуральную величину.

Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими.

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций П1 (рис.5).

Горизонтально-проецирующая плоскость задается горизонтальным следом плоскости ∑1

Углы наклона горизонтально-проецирующей плоскости к П2 и П3 проецируются на горизонтальную плоскость проекций в натуральную величину.

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций П2, задается фронтальным следом плоскости ∆2 (рис.6).

Проекции всех линий и точек, лежащих во фронтально-проецирующей плоскости, совпадают с фронтальным следом этой плоскости. Углы наклона фронтально-проецирующей плоскости к П1 и П3 проецируются на фронтальную плоскость проекций в натуральную величину.

Источник

Плоскости частного и общего положения

Плоскость и ее задание на чертеже

Лекция №2. Плоскость. Позиционные и метрические задачи на плоскости

Плоскость является простейшей поверхностью, которую можно представить как веер линий, полученных при движении прямой (образующей), закрепленной в некоторой точке, по другой прямой (направляющей). В дальнейшем мы увидим, что и образующая, и направляющая могут быть не прямыми линиями.

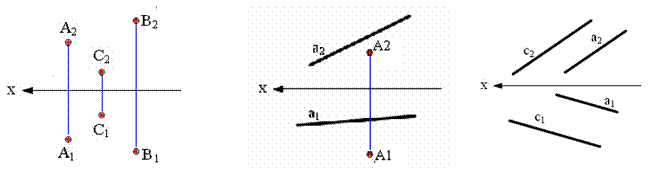
Положение плоскости в пространстве может быть однозначно определено одним из хорошо известных в геометрии элементов (прямой и точкой). В соответствии с этим плоскость может быть задана одним из шести способов:

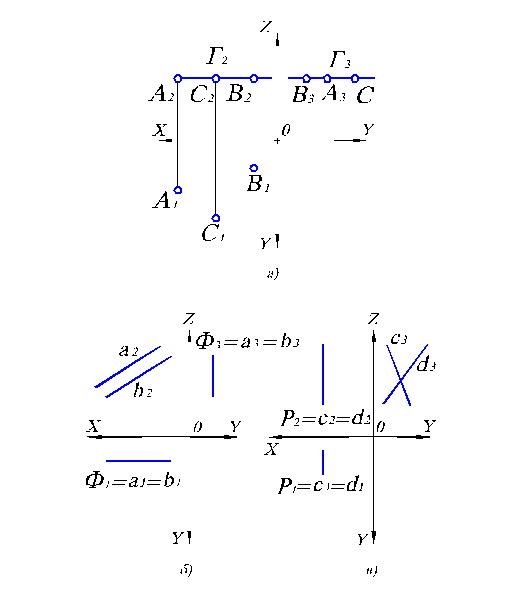
а) тремя точками, не лежащими на одной прямой;

б) прямой и точкой, не лежащей на этой прямой;

в) двумя параллельными прямыми;

г) двумя пересекающимися прямыми;

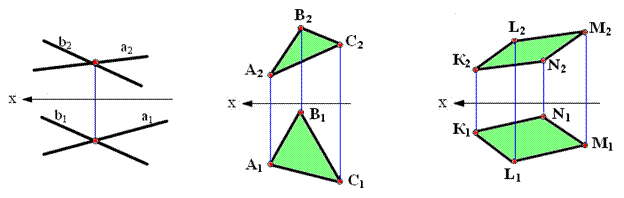
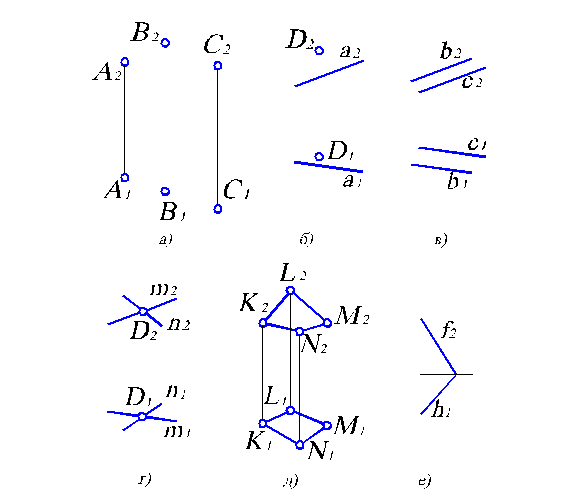
Тогда на чертеже (рис. 2.1) проекции плоскости выглядят, как проекции соответствующих геометрических объектов — точек и прямых, — которыми они заданы.

Рис. 2.1. Безосный двухкартинный комплексный чертеж геометрических объектов, задающих плоскость.

Плоскостью частного положения называется плоскость, занимающая частное положение в пространстве, т.е. параллельная или перпендикулярная одной из плоскостей проекций.

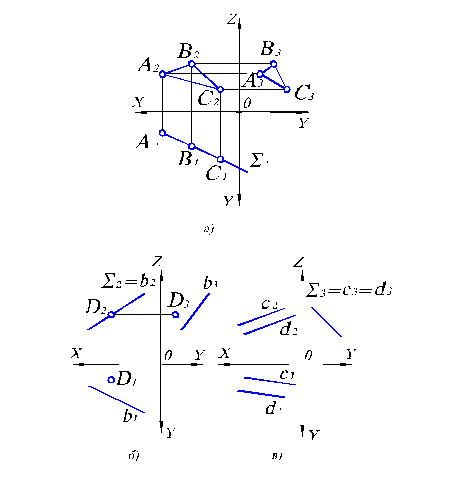
Плоскостью уровня называется плоскость, параллельная одной из плоскостей проекций, а следовательно, перпендикулярная двум другим. Тогда проекциями плоскости уровня будут прямые, параллельные соответствующим осям (рис. 2.2), вне зависимости от того, чем задана плоскость. От способа задания плоскости зависит лишь ее проекция на ту плоскость проекций, которой заданная плоскость параллельна.

Рис. 2.2. Плоскости уровня на комплексном чертеже.

Плоскость, параллельная П₂, называется фронтальной плоскостью уровня ( Ф ). Зададим ее параллельными прямыми (рис. 2.2, б). Причем, очевидно, расстояние от Ф₁ до ОХ равно расстоянию от Ф₃ до ОZ.

Плоскость, параллельная П₃, называется профильной плоскостью уровня ( Р ). Считаем ее заданной пересекающимися прямыми (рис. 2.2, в).

Проецирующей называется плоскость, перпендикулярная одной из плоскостей проекций. Исходя из определения, такая плоскость вырождается в прямую при проецировании на ту плоскость проекций, к которой она перпендикулярна.

Рис. 2.3. Проецирующие плоскости на комплексном чертеже.

Плоскость общего положения

Плоскостью общего положения называется плоскость, не перпендикулярная и не параллельная ни одной из плоскостей проекций, а значит, расположенная под произвольным углом к каждой из них.

У такой плоскости все проекции будут невырожденные. Например, если плоскость общего положения задана плоской фигурой (треугольником), то все три проекции ее будут треугольниками (рис. 2.4).

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

2.6. Частные положения плоскостей в пространстве

Плоскость общего положения

Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций – произвольные, но отличные от 0° и 90°) называется плоскостью общего положения (рис. 2.16.а).

На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.

Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекции.

Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости).

1. Горизонтально-проецирующая плоскость aπ₁.

.

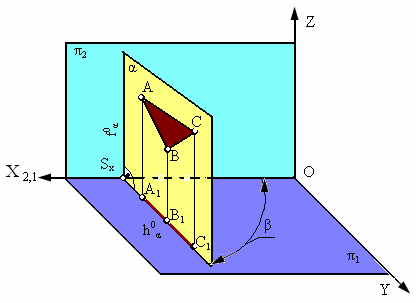
Рис. 2.13. Горизонтально-проецирующая плоскость

Плоскость α, перпендикулярная горизонтальной плоскости проекции π₁, называется горизонтально-проецирующей (рис. 2.13).

Основным свойством горизонтально-проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π₁ в прямую линию (горизонтальный след плоскости h_0a).

Угол β, который составляет горизонтальный след плоскости h_0a c координатной осью Х, равен углу наклона плоскости a к плоскости проекций π₂. Фронтальный след такой плоскости перпендикулярен оси Х (f_0a X).

2. Фронтально-проецирующая плоскость β π₂. Плоскость b перпендикулярная фронтальной плоскости проекций π₂ называется фронтально проецирующей (рис. 2.14).

.

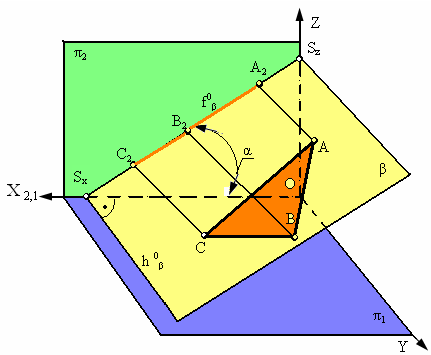
Рис. 2.14. Фронтально-проецирующая плоскость

Основным свойством фронтально-проецирующей плоскости является то, что любая фигура. Расположенная в этой плоскости, проецируется на π₂ в прямую линию (фронтальный след плоскости f_0b). Угол α, который составляет фронтальный след плоскости f_0b с координатной осью Х, равен углу наклона плоскости β к плоскости проекций π₁. Горизонтальный след такой плоскости перпендикулярен оси Х.

Плоскости, параллельные плоскостям проекций (плоскости уровня)

1. Горизонтальная плоскость γ π₁.

Плоскость γ, параллельная плоскости π₁, называется горизонтальной (рис. 2.15).

.

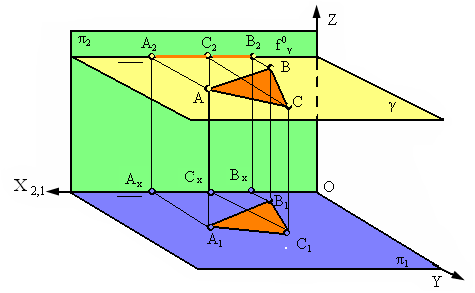
Рис. 2.15. Плоскость, параллельная горизонтальной плоскости проекций

Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость проекций в натуральную величину (Δ А₁В₁С₁= ΔАВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f_0γХ).

2. Фронтальная плоскость δ π₂.

Плоскость δ, параллельная плоскости π₂, называется фронтальной.

Любая фигура расположенная в такой плоскости. Проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.

Горизонтальный след фронтальной плоскости параллелен оси Х.

Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.

Источник