Что такое плоскость прямая луч отрезок
Математика. 5 класс
Конспект урока
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.
Плоскость. Прямая. Луч
Урок 4. Математика 5 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Плоскость. Прямая. Луч»
На этом уроке мы познакомимся с понятиями «отрезок», «прямая», «луч» и «плоскость». Рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
На прошлом уроке мы разобрались, как строить отрезок. Мы уже знаем, что отрезок – это прямая линия, ограниченная двумя точками.
Давайте начертим отрезок MN. Если продлить этот отрезок неограниченно за точку N, то мы получим новую фигуру, которая называется луч. У нас получился луч MN.
Точку М называют началом луча.
Если бы мы продлевали отрезок MN неограниченно за точку М, то у нас бы получился луч NМ, у которого точка N – начало луча.
Заметьте: обозначается луч большими заглавными буквами латинского алфавита, первой буквой записывают его начало, а затем букву, обозначающую какую-либо другую точку луча.
Обратите внимание, что луч имеет начало, но не имеет конца, т. е. он бесконечен в одну сторону.
Для того чтобы представить луч в окружающей среде, достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт – это начальная точка, а след, оставленный на небе, – это прямая линия, которая бесконечна.
Либо солнечный луч, где начальная точка – это солнце, а конечной точки нет.
Если отрезок MN неограниченно продлевать в обе стороны – как за точку М, так и за точку N, то у нас получится фигура, которая называется прямой.
На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!
Заметьте, что прямая не имеет ни начала, ни конца.
Любая точка прямой разделяет её на 2 луча.
В нашем случае точка О разделяет прямую MN на луч ОМ и луч ОN. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.
Представление о прямой можно получить, если сложить лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго натянуть верёвку.
В математике прямая представляется идеально ровной и бесконечной в обе стороны.
Прямую можно обозначить двумя вариантами.
1-й вариант: двумя заглавными буквами латинского алфавита, например MN. В таком случае говорят: «Прямая MN».
2-й вариант: прямую обозначают одной малой буквой, например m, и говорят: «Прямая m».
Давайте попробуем провести ещё одну прямую через эти же две точки.
У нас это не получится. Через любые две точки можно провести только одну прямую!
Точки, отрезки, лучи и прямые располагаются в плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.
Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях. Мы рисуем фигуры на «кусках» плоскости, например в тетрадном листе или на школьной доске.
Теперь давайте рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
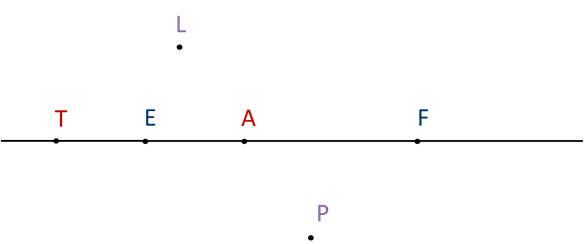
На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на отрезке EF, а точки L, P, T не лежат на этом отрезке. Посмотрите, как это записывается.
Точки А, E, F лежат на луче EF, а точки А, E, F, Т лежат на луче FЕ. Посмотрите запись этих утверждений.
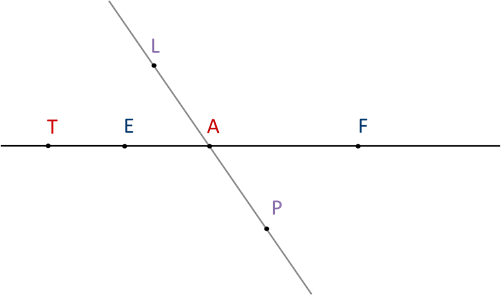
Точки А, E, F, Т лежат на прямой EF, а точки А, P, L – на прямой PL.
Обозначается это так:
Точка А лежит между точками Е и F. Точка L не лежит между точками Е и F, она находится вне отрезка EF. Точка Е лежит между точками А и Т, а точка А – между точками P и L.
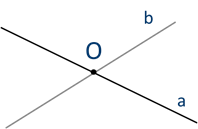
На следующем рисунке изображены прямая a и прямая b.
Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются в точке О. Точка О делит каждую прямую на две части. Точка О – точка пересечения прямых.
Посмотрите на взаимное расположение прямых m и n:
Они не имеют общих точек. Если прямые не имеют общих точек, то говорят, что они параллельны.
· Луч имеет начало, но не имеет конца.
Итак, на уроке мы с вами разобрались в отличиях понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в плоскости.
Урок 4 Бесплатно Плоскость. Прямая. Луч
В этом уроке мы продолжим разговор про геометрию, начатый в прошлых уроках.
Мы рассмотрим такие понятия, как плоскость, прямая, луч, поговорим еще раз про отрезки. Также обсудим, как все эти объекты могут располагаться друг относительно друга. Начнем же.
Плоскость
Важно отметить, что в начале разбора приходится некоторые понятия принимать как нечто, что не требует определения, к таким понятиям относятся понятия прямой и точки.
Немецкий учений Гильберт как-то сказал на эту тему, что “точкой можно назвать хоть стул”, тем самым говоря, что вся наша модель строится на некоторых условностях.
С этим пониманием приступим к первой теме урока.
Для начала нам нужно понять, что такое поверхность.
Есть много строгих математических формулировок, но они уместны скорее в высших учебных заведениях, пока будет достаточно обиходного понятия поверхности.
Будем понимать под поверхностью непрерывное множество точек, границу, отделяющую геометрическое тело от внешнего пространства.
Представьте себе поверхность рабочего стола, футбольного мяча или любого другого предмета.
Также известно, что некоторые поверхности, например, рабочего стола, плоские.
Плоская в данном случае обозначает, что если через любые две точки, принадлежащие этой плоскости, провести прямую, то она будет лежать в этой плоскости.
В самом деле, если нарисовать две точки на поверхности стола и соединить их прямой, то эта прямая будет лежать в плоскости стола.
Если же отметить две точки на шаре, то (тут нужен некоторый мысленный эксперимент) прямая, соединяющая их, будет проходить внутри шара, а не по его поверхности. Таким образом, поверхность шара не плоская, не является плоскостью.
Обычно на рисунках плоскость обозначается конечной, в крайнем случае лист бумаги или экран компьютера конечен.
Но это лишь обозначения, сама плоскость бесконечна.
Поверхности и плоскости принято обозначать двумя способами: с помощью трех латинских букв, соответствующих трем точкам плоскости, или одной греческой.
Выше изображена четырехугольная пирамида. В ней можно насчитать 5 плоскостей:
Согласись, две точки слишком мало, чтобы обозначить плоскость: на данном рисунке, например, есть две плоскости, проходящие через точки A и E, а четыре точки уже несут избыточную информацию, поэтому плоскости обозначают тремя точками.
Иногда плоскость обозначают одной строчной греческой буквой, например, так:
Точка может принадлежать плоскости (лежать в ней) или не принадлежать плоскости.
Пройти тест и получить оценку можно после входа или регистрации
Прямая
Проведем отрезок, назовем его AB.
А теперь продолжим его по линейке за концы в обе стороны:
Так мы получим прямую. Прямая, как и плоскость, бесконечна.
Если плоскость простирается во все стороны, то прямая в конкретные два направления.
Как и в случае с плоскостью, невозможно изобразить нечто бесконечное в тетрадях или на мониторах, так как эти объекты имеют границы, поэтому любое изображение будет лишь обозначать прямую.
Для обозначения прямой используются две заглавные латинские буквы, так выше приведенную прямую можно назвать “прямая АВ” или “прямая ВА”.
Также иногда прямые обозначают строчными латинскими буквами:
Вот, например, прямая а.
Через любые две точки проходит единственная прямая.
То есть ситуация, при которой между двумя точками нет ни одной прямой или, напротив, более одной, невозможна.
Так на рисунке выше точки А и В принадлежат прямой АВ.
Рассмотрим другой рисунок:
В данном случае точки С и D не принадлежат прямой АВ.
Мы можем представить себе прямую, нарисованную на плоском листе бумаги.
Так и в математике прямые могут принадлежать плоскостям.
Можно изобразить это так:
На рисунке прямая а, принадлежит плоскости \(\mathbf<\alpha>\)
Обычно такие рисунки сопровождают текстовым описанием для того, чтобы их понимали однозначно.
Также мы можем видеть прямые и на других рисунках.
Мы знаем, что через любые две точки проходит прямая.
Так что смотря на рисунок выше мы можем говорить про прямые AE, ED, DC, AC, AB, EB, DB, CB
Точно также можно видеть прямые не только на объемных рисунках, но и на плоских.
Так на этом рисунке можно говорить про прямые AB, BC и AC
Также отношение “принадлежит” обладает в данном случае таким свойством: если точка принадлежит прямой, а прямая принадлежит плоскости, то верно, что эта точка принадлежит плоскости.
Посмотрим на рисунок:
Если нам известно, что точка А принадлежит прямой а и прямая а принадлежит плоскости \(\mathbf<\alpha>\), то очевидно, что и сама точка А принадлежит прямой \(\mathbf<\alpha>\)
Про прямые надо знать такое определение:
Если две прямые имеют общую точку, то говорят, что они пересекаются в этой точке.
В данном случае это точка О.
Пройти тест и получить оценку можно после входа или регистрации
Любая точка на прямой делит ее на две части.
Каждую из этих частей называют лучом.
Сама такая точка будет называться началом луча.
Точка М является началом обоих лучей.
Лучи МА и МВ называются дополнительными друг другу. Это такие лучи, на которые точка разбивает прямую.
Давая лучам название, первой буквой пишут вершину луча, вторая определяет направление.
Это может быть как точка на соответствующей прямой, так и просто буква, подписанная возле соответствующей части прямой, как на рисунке выше.
Как и в случае с прямой, точки могут лежать и не лежать на луче.
Посмотрим, как лежат точки относительно луча MB.
Точки Р и К не лежат на прямой АВ, значит и на луче, как на части прямой, лежат не могут.
Точка С не лежит на луче МВ, так как находится с другой стороны от точки М, луч уходит в сторону В.
Научимся видеть лучи еще в некоторых ситуациях.
Например, сколько лучей образуются при пересечении прямых?
Обозначим прямые как АВ и CD, точку пересечения назовем точкой О.
Имеем одну точку, которая может стать началом луча, от нее отходят четыре половины прямых.
А полупрямая это и есть луч. Значит, при пересечении двух прямых от точки их пересечения будет отходить 4 луча.
Посмотрим еще раз на картинку с треугольником АВС.
В случае с лучом принципиально, где у него начало, а где продолжение (конца не бывает).
Тогда у нас есть 3 точки-кандидата на начало луча. От каждой точки отходит по два отрезка, но чтобы обозначить луч нам нужна любая точка с продолжения, так что получается, что от каждой вершины отходят по 2 луча и всего на рисунке можно увидеть 6 лучей, если не ставить дополнительных точек.
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Геометрия, про которую мы сегодня говорили, называется Евклидовой.
Как уже было сказано, часть понятий является фундаментальными. В данном случае первоначальные понятия Евклидовой геометрии предложил, как следует из названия, Евклид, живший в Древней Греции.
Если быть более точным, жил он в Александрии и являлся первым математиком Александрийской школы.
О самом Евклиде, к сожалению, известно крайне мало информации.
Самая его известная книга “Начала” содержала в себе факты о геометрии, а также об арифметике.
Иногда книга издавалась с комментариями. Из одного из таких изданий с комментариями от Прокла мы знаем что-то про Евклида, хотя Прокл жил примерно на 800 лет позже Евклида.
Также существуют скульптуры и портреты, посвященные Евклиду, но есть сомнения в их достоверности.
По сути единственное, что известно более-менее точно, так это то, что ученые занимались вопросами геометрии еще в те времена.
Сохранились и другие работы Евклида, например, ему приписывают “Деление канона” (трактат о теории музыки), но им уделяется меньше внимания.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Плоскость, прямая линия, луч
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Обозначение прямой
Например, на рисунке 1 обозначены такие прямые:
Рис. 1 Обозначение прямой линии
Рис. 2 Обозначение прямой с несколькими точками
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
Рис. 5 Пересечение прямых
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
Луч имеет второе название – полупрямая.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 22