Что такое плоскость уровня

Что такое плоскость уровня

Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня. Как и проецирующие плоскости, плоскости уровня задаются следами. Все объекты, лежащие в плоскости уровня, проецируются на параллельную плоскость проекций в натуральную величину.

Горизонтальная плоскость уровня ν ∥ П₁ – плоскость, параллельная горизонтальной плоскости проекций (рис. 41).

Треугольник ABC, лежащий в горизонтальной плоскости уровня, проецируется на П₁ в натуральную величину (рис. 42).

Фронтальная плоскость уровня μ ∥ П₂ – плоскость, параллельная фронтальной плоскости проекций (рис. 43).

На рис. 44 показана окружность l с центром в точке О и диаметром AB, лежащая во фронтальной плоскости уровня μ(μ₁). Эта окружность проецируется на П₂ без искажения.

Профильная плоскость уровня ω∥ П₃ – плоскость, параллельная профильной плоскости проекций (рис. 45).

Отрезок [AB], лежащий в профильной плоскости уровня ω(ω₁), проецируется на плоскость П₃ в натуральную величину (рис. 46).

Источник

Что такое плоскость уровня

В зависимости от положения относительно плоскостей проекций различают плоскости общего положения и плоскости частного положения.

Плоскость общего положения – плоскость, наклоненная под произвольными углами к плоскостям проекций (рис.1).

Плоскости частного положения можно разделить на две группы – проецирующие плоскости и плоскости уровня. Плоскости частного положения чаще всего задаются следами.

Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня. Все объекты, лежащие в плоскости уровня, проецируются на параллельную плоскость проекций в натуральную величину.

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (рис.2).

Треугольник ABC, лежащий в горизонтальной плоскости уровня, проецируется на П1 в натуральную величину.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (рис. 3).

Треугольник ABC, лежащий во фронтальной плоскости уровня, проецируется на П2 в натуральную величину.

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (рис. 4).

Треугольник ABC, лежащий в профильной плоскости уровня, проецируется на плоскость П3 в натуральную величину.

Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими.

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций П1 (рис.5).

Горизонтально-проецирующая плоскость задается горизонтальным следом плоскости ∑1

Углы наклона горизонтально-проецирующей плоскости к П2 и П3 проецируются на горизонтальную плоскость проекций в натуральную величину.

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций П2, задается фронтальным следом плоскости ∆2 (рис.6).

Проекции всех линий и точек, лежащих во фронтально-проецирующей плоскости, совпадают с фронтальным следом этой плоскости. Углы наклона фронтально-проецирующей плоскости к П1 и П3 проецируются на фронтальную плоскость проекций в натуральную величину.

Источник

Статьи о радиотехнике, технологиях, чертежах, 3D-моделировании

Публикации для людей, интересующихся наукой и техникой

ПЛОСКОСТЬ – является простейшей поверхностью, которую можно представить, например, как веер линий, полученных при движении прямой, закрепленный в некоторой (.), по другой прямой

В отличие от линии, плоскость не может быть задана на чертеже своими проекциями. Плоскость в пространстве безгранична, бесконечна, а потому проекции её (.) займут всё поле чертежа. Положение плоскости в пространстве определяется положением задающихся ее элементов, входящих в определитель плоскости, т.е. плоскость задается проекциями геометрических объектов, располагающихся на ее поверхности. Графически плоскость может быть задана одним из шести способов:

От любого из этих способов можно легко перейти к любому другому.

СЛЕДЫ ПЛОСКОСТИ (сп) – пл, по которой данная плоскость пересекается с горизонтальной, фронтальной или профильной пп. В зависимости от того, какую пп данная плоскость пересекает, различают: фронтальный, горизонтальный и профильный следы плоскости. Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие – разноименные проекции – оказываются лежащими на осях координат. Проекции следов, совпадающие с осями координат, обозначать не принято. Любые два следа плоскости, как две пересекающиеся прямые, вполне определяют положение плоскости в пространстве. Третий след плоскости всегда можно построить по двум данным. След плоскости как линия в системе пп является линией нулевого уровня, т.к. принадлежит поверхности какой-либо плоскости проекций.

ТОЧКИ СХОДА СЛЕДОВ (тсс) – точки пересечения следов заданной плоскости с координатными осями X, Y и Z. Обозначаются, например, для плоскости α соответственно αx, αy, αz.

ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ (поп) – это плоскость, занимающая произвольное положение относительно плоскостей проекций, т.е. она не ⟂ и не ∥ ни одной основной плоскости проекций. Ни одна из ортогональных проекций геометрических объектов, задающих плоскость общего положения, не сливается в пл. Метрические характеристики такой плоскости на чертеже искажаются и не могут быть определены непосредственно с чертежа плоскости. Различают: восходящие и нисходящие плоскости общего положения.

ВОСХОДЯЩАЯ ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ (впоп) – плоскость произвольного положения, которая, удаляясь от наблюдателя, идет вверх (на подъем). Метрические характеристики данной плоскости на чертеже напрямую не определяются. Угол наклона такой плоскости можно получить с использованием линии ската.

НИСХОДЯЩАЯ ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ (нпоп) – плоскость произвольного положения, которая, удаляясь от наблюдателя, идет вниз (на спуск). Метрические характеристики данной плоскости на чертеже напрямую не определяются. Угол наклона такой плоскости можно получить с использованием линии ската.

ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ (пчп) – это плоскости, ⟂ либо ∥ пп. Различают: проецирующие плоскости и плоскости уровня. На ортогональном чертеже любой плоскости частного положения хотя бы одна проекция всегда вырождается в пл.

ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (пп) – это плоскость, ⟂ к одной из пп и при этом не ⟂ и не ∥ двум другим. В зависимости от того к какой плоскости проекций ⟂ проецирующая плоскость, различают: горизонтально проецирующую, фронтально проецирующую и профильно проецирующую плоскости.

ГОРИЗОНТАЛЬНО ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (гпп) – плоскость, ⟂ горизонтальной плоскости проекций П₁ и при этом не ⟂ и не ∥ фронтальной П₂ и профильной П₃ плоскостям проекций. Гпп представляет собой прямую линию, которая одновременно является гcп. Любой геометрический объект, расположенный в этой плоскости, проецируется на горизонтальной плоскости проекций П₁ в эту прямую. Угол, который составляет гсп с координатной осью Х, равен углу наклона этой плоскости к фронтальной плоскости проекций П₂, а с координатной осью Y– к профильной плоскости проекций П₃. Фронтальный след гпп ⟂ оси координат X.

ФРОНТАЛЬНО ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (фпп) – плоскость, ⟂ фронтальной плоскости проекций П₂ и при этом не ⟂ и не ∥ горизонтальной П₁ и профильной П₃ плоскостям проекций. Фпп представляет собой прямую линию, которая одновременно является фсп. Любой геометрической объект, лежащий в этой плоскости, на чертеже совмещен с ее фронтальным следом. Угол, который составляет фсп с координатной осью Х, равен наклону данной плоскости к горизонтальной плоскости проекций П₁, а с координатной осью Z – к профильной плоскости проекций П₃. Горизонтальный след фронтально проецирующей плоскости перпендикулярен оси координат Х.

ПРОФИЛЬНО ПРОЕЦИРУЮЩАЯ ПЛОСКОСТЬ (ппп) – плоскость, ⟂ профильной плоскости проекций П₃ и при этом не ⟂ и не ∥ горизонтальной П₁ и фронтальной П₂ плоскостям проекций. Ппп представляет собой прямую линию, которая одновременно является профильным следом плоскости. Любой геометрический объект, лежащий в этой плоскости, на чертеже совмещен с ее профильным следом. Угол, который составляет псп с координатной осью Y, равен наклону данной плоскости к горизонтальной плоскости проекций П₁, а с координатной осью Z – к фронтальной плоскости проекций П₂. Горизонтальный след такой плоскости перпендикулярен оси Y. В зависимости от удаления от наблюдателя различают: восходящую профильно проецирующую и нисходящую ппп.

ПЛОСКОСТЬ УРОВНЯ (пу) – это плоскость ∥ одной из плоскостей проекций, а значит ⟂ одновременно к двум другим плоскостям проекций. В зависимости от того какой плоскости проекций параллельна данная плоскость, различают: горизонтальную, фронтальную и профильную плоскости уровня. Любой геометрический объект, расположенный в плоскости уровня, в зависимости от параллельности проецирует на одну из плоскостей проекций в натуральную величину.

ГОРИЗОНТАЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ (гпу) – плоскость, ∥ гпп П₁ и при этом ⟂ фронтальной П₂ и профильной П₃ плоскостям проекций. Фронтальная и профильная проекции такой плоскости – прямые линии, совпадающие с одноименными следами этой плоскости, и ∥ осям координат X и Y соответственно. Любой геометрический объект, расположенный в гпу, проецируется без искажения на гпп П₁.

ФРОНТАЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ (фпу) – плоскость, ∥ фронтальной плоскости проекций П₂ и при этом ⟂ горизонтальной П₁ и профильной П₃ плоскостям проекций. Горизонтальная и профильная проекции такой плоскости – прямые линии, совпадающие с одноименными следами этой плоскости и ∥ осям координат Х и Z соответственно. Любой геометрический объект, расположенный во фпу, проецируется без искажения на фронтальную плоскость проекций П₂.

ПРОФИЛЬНАЯ ПЛОСКОСТЬ УРОВНЯ (ппу) – плоскость, ∥ профильной плоскости проекций П₃ и при этом ⟂ горизонтальной П₁ и фронтальной П₂ плоскостям проекций. Горизонтальная и фронтальная проекции такой плоскости – прямые линии, совпадающие с одноименными следами этой плоскости и ∥ осям координат Y и Z соответственно. Любой геометрический объект, расположенный в ппу, проецируется без искажения на ппп П₃.

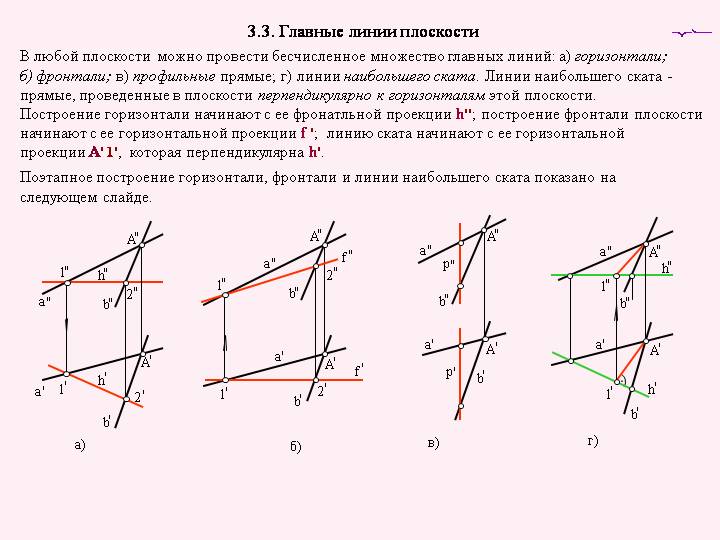
ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ (глп) – это пл, расположенные в данной плоскости, выделяемые среди множества других линий, как занимающие особое положение. Это линии уровня плоскости: горизонталь h, фронталь f и ппп p, а также линии наибольшего наклона плоскости к плоскостям проекций П₁, П₂ и П₃.

ГОРИЗОНТАЛЬ ПЛОСКОСТИ (гп) – пл, принадлежащая этой плоскости и ∥ гпп П₁, т.е. это горизонтальная прямая линия уровня, лежащая на поверхности какой-либо плоскости. Фронтальная и профильная проекции горизонтали плоскости ∥ осям координат X и Y соответственно Все горизонтали плоскости ∥ друг другу и горизонтальному следу своей плоскости. Обозначается на чертеже буквой – h.

ФРОНТАЛЬ ПЛОСКОСТИ (фп) – пл, принадлежащая этой плоскости и ∥ фпп П₂, т.е. это фронтальная прямая линия уровня, лежащая на поверхности какой-либо плоскости. Горизонтальная и профильная проекции фронтали плоскости ∥ осям координат X и Z соответственно. Все фронтали плоскости параллельны друг другу и фронтальному следу своей плоскости. Обозначается на чертеже буквой – f.

ПРОФИЛЬНАЯ ПРЯМАЯ ЛИНИЯ ПЛОСКОСТИ (пплп) – пл, принадлежащая этой плоскости и параллельная профильной плоскости проекций П₃, т.е. это профильная прямая линия уровня, лежащая на поверхности какой-либо плоскости. Фронтальная и горизонтальная проекции профильной прямой плоскости параллельны осям координат Z и Y соответственно. Все профильные прямые линии плоскости параллельны друг другу и профильному следу своей плоскости. Обозначается на чертеже буквой – p.

ЛИНИИ НУЛЕВОГО УРОВНЯ ПЛОСКОСТИ (лнуп) – это пл, принадлежащие одновременно данной плоскости и какой-либо плоскости проекций, т.е. являются одновременно и главными линиями плоскости, и следами этой плоскости. Горизонтальный след плоскости – это горизонталь плоскости нулевого уровня, фронтальный след плоскости – фронталь плоскости нулевого уровня и профильный след плоскости – профильная прямая плоскости нулевого уровня. Обозначаются на чертеже – h_оά, f_оά, ρ_оά соответственно.

ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ (лннп) к плоскостям проекций П₁, П₂ и П₃ – пл, лежащие в ней и ⟂ или к горизонталям плоскости, или к ее фронталям, или к ее профильным прямым.

ЛИНИЯ СКАТА ПЛОСКОСТИ (лсп) – линия наибольшего наклона плоскости к гпп П₁, т.е. пл, проведенная по поверхности плоскости ⟂ любой горизонтали этой плоскости. Согласно теореме о проекции прямого угла, прямой угол между горизонталью плоскости и линией ската плоскости проецируется на гпп П₁ без искажения. Лсп и ее горизонтальная проекция образуют линейный угол, которым измеряется двугранный, составленный данной плоскостью и пп П₁.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ К ФРОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ П₂ (лннпкфпп) – пл, проведенная по поверхности какой-либо плоскости ⟂ любой фронтали этой плоскости. Согласно теореме о проекции прямого угла, прямой угол между лннпкфпп П₂ и фронталью этой плоскости проецируется на фронтальную плоскость проекций П₂ без искажения.

ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ К ПРОФИЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ П₃ (лннпкппп) – пл, проведенная по поверхности плоскости перпендикулярно профильной прямой линии уровня этой плоскости. Согласно теореме о проекции прямого угла, прямой угол между лннпкппп П₃ и профильной прямой линией этой плоскости проецируется на профильную плоскость проекций П₃ без искажения.

Если у вас остались вопросы или предложения по данной статье, направляйте ваш материал к нам на контакты.

Источник

Плоскости уровня

Характеристика	Наглядное изображение	Эпюр
Фронтальнаяплоскость – это плоскость, параллельная плоскости p2. Эта плоскость пересекает плоскость p1 параллельно оси ОХ, а плоскость p3 – по линии, параллельной оси OZ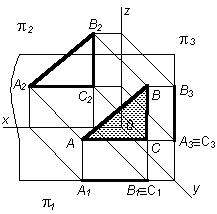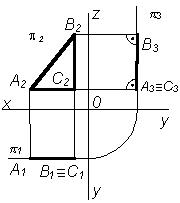
Горизонтальная плоскость – это плоскость, параллельная плоскости проекции p1. Эта плоскость пересекает плоскость p2 параллельно оси ОХ, а плоскость p3 – параллельно оси ОУ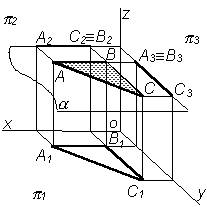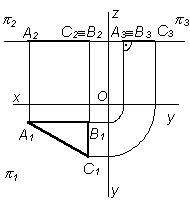
Профильная плоскость – это плоскость, параллельная плоскости p3. Эта плоскость пересекает плоскости проекций p1 и p2 по линиям, параллельным оси Z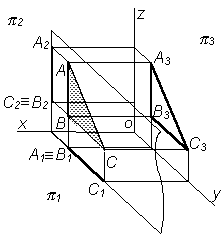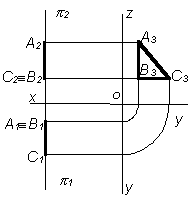

11. Назовите главные линии плоскости Изобразите их

12. поясните, какое взаимное положение могут занимать плоскость и пряма, две плоскости. Назовите признаки взаимного положения. Рассмотрите пример построения на комплексном чертеже.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости. Чтобы построить такую прямую, необходимо в плоскости задать любую прямую и параллельно ей провести требуемую.

Рис. 1.53 Рис. 1.54 Рис.1.55

Из всех возможных положений прямой, пересекающей плоскость, отметим случай, когда прямая перпендикулярна плоскости. Рассмотрим свойства проекций такой прямой.

Прямая перпендикулярна плоскости(частный случай пересечения прямой с плоскостью) если она перпендикулярна какой-либо прямой, лежащей в плоскости. Для построения проекций перпендикуляра к плоскости, находящейся в общем положении, этого недостаточно без преобразования проекций. Поэтому вводят дополнительное условие: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся главным линиям (для построения проекций используется условие проецирования прямого угла). В этом случае: горизонтальная и фронтальная проекции перпендикуляра перпендикулярны соответственно горизонтальной проекции горизонтали и фронтальной проекции фронтали данной плоскости общего положения (рис. 1.54). При задании плоскости следами проекции перпендикуляра перпендикулярны соответственно фронтальная – фронтальному следу, горизонтальная – горизонтальному следу плоскости (рис. 1.55).

Пересечение прямой с проецирующей плоскостью.Рассмотрим прямую, пересекающую плоскость, когда плоскость находится в частном положении.

Плоскость, перпендикулярная плоскости проекций (проецирующая плоскость), проецируется на нее в виде прямой линии. На этой прямой (проекции плоскости) должна находиться соответствующая проекция точки, в которой некоторая прямая пересекает эту плоскость (рис.1.56).

На рисунке 1.56 фронтальная проекция точки К пересечения прямой АВ с треугольником СDE определяется в пересечении их фронтальных проекций, т.к. треугольник СDE проецируется на фронтальную плоскость в виде прямой линии. Находим горизонтальную проекцию точки пересечения прямой с плоскостью ( она лежит на горизонтальной проекции прямой). Способом конкурирующих точек, определяем видимость прямой АВ относительно плоскости треугольника СDE на горизонтальной плоскости проекций.

На рисунке 1.59 изображена горизонтально-проецирующая плоскость P и прямая общего положения АВ. Т.к. плоскость Р перпендикулярна горизонтальной плоскости проекций, то все, что в ней находится, на горизонтальную плоскость проекций проецируется на ее след, в том числе и точка ее пересечения с прямой АВ. Следовательно, на комплексном чертеже имеем горизонтальную проекцию точки пересечения прямой с плоскостью Р. По принадлежности точки прямой, находим фронтальную проекцию точки пересечения прямой АВ с плоскость Р. Определяем видимость прямой на фронтальной плоскости проекций.

На рисунке 1.58 дан комплексный чертеж построения проекций точки пересечения прямой АВ с плоскостью горизонтального уровня G.Фронтальный след плоскости G является ее фронтальной проекцией. Фронтальная проекция точки пересечения плоскости G с прямой АВ определятся в пересечении фронтальной проекции прямой и фронтального следа плоскости. Имея фронтальную проекцию точки пересечения, находим горизонтальную проекцию точки пересечения прямой АВ с плоскостью G.

Пересечение двух плоскостей.Прямая линия пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плоскостям, или одной точкой, принадлежащей двум плоскостям, и известным направлением линии. В обоих случаях задача заключается в нахождении точки, общей для двух плоскостей.

Пересечение проецирующих плоскостей.Две плоскости могут быть параллельны между собой или пересекаться. Рассмотрим случаи взаимного пересечения плоскостей.

Прямая линия, получаемая при взаимном пересечении двух плоскостей, вполне определяется двумя точками, из которых каждая принадлежит обеим плоскостям, следовательно, необходимо и достаточно найти эти две точки, принадлежащей линии пересечения двух заданных плоскостей.

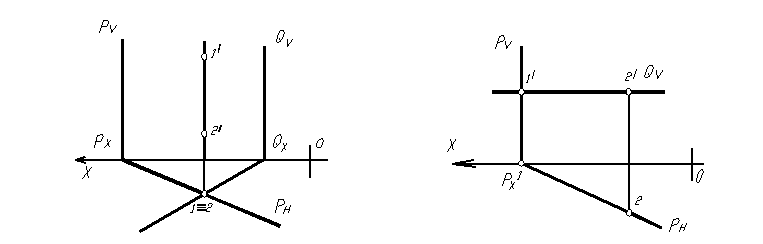
Следовательно, в общем случае для построения линии пересечения двух плоскостей необходимо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям. Эти точки и определяют линию пересечения плоскостей. Для нахождения каждой из этих двух точек обычно приходится выполнять специальные построения. Но если хотя бы одна из пересекающихся плоскостей перпендикулярна (или параллельна) к какой-либо плоскости проекций, то построение проекции линии их пересечения упрощается.

Рассмотрим частные случаи расположения одной (или обеих) из пересекающихся плоскостей.

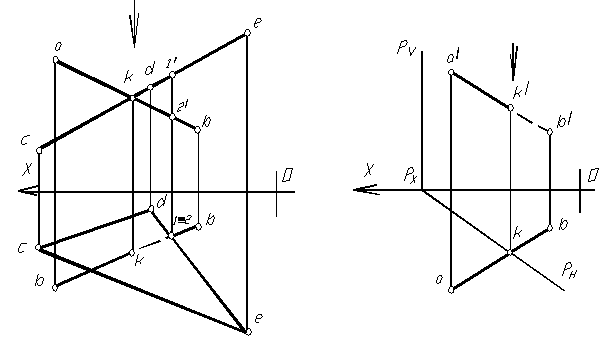
На комплексном чертеже (рис.1.60) изображены горизонтально-проецирующие плоскости P и Q. Тогда горизонтальная проекция их линии пересечения вырождается в точку, а фронтальная проекция – в прямую, перпендикулярную оси оx.

В случае задания плоскостей следами легко установить, что эти плоскости пересекаются: если хотя бы одна пара одноименных следов пересекается, то плоскости пересекаются между собой.

Изложенное относится к плоскостям, заданных пересекающимися следами. Если же обе плоскости имеют на горизонтальной и фронтальной плоскостях следы, параллельные друг другу, то эти плоскости могут быть параллельны либо пересекаться. О взаимном положении таких плоскостей можно судить, построив третью проекцию (третий след). Если следы обеих плоскостей на третьей проекции так же параллельны, то плоскости параллельны между собой. Если следы на третьей плоскости пересекаются, то заданные в пространстве плоскости пересекаются.

На комплексном чертеже (рис.1.62) изображены фронтально-проецирующие плоскости, заданные треугольником АВС и DEF. Проекция линии пересечения на фронтальной плоскости проекций – точка, т.е. так как треугольники перпендикулярны фронтальной плоскости проекций, то и их линия пересечения так же перпендикулярна фронтальной плоскости проекций. Следовательно горизонтальная проекции линии пересечения треугольников (12) перпендикулярна оси оx. Видимость элементов треугольников на горизонтальной плоскости проекции определяется с помощью конкурирующих точек (3,4).

На комплексном чертеже (рис. 1.63) заданы две плоскости: одна из которых треугольником АВС общего положения, другая – треугольником DEF перпендикулярна фронтальной плоскости проекций, т.е. находящийся в частном положении (фронтально-проецирующий). Фронтальная проекция линии пересечения треугольников (1 / 2 / ) находится исходя из общих точек, одновременно принадлежащих обоим треугольникам (все, что находится во фронтально- проецирующем треугольнике DEF на фронтальной проекции выльется в линию – проекцию его на фронтальную плоскость, в том числе и линия его пересечения с треугольником АВС. По принадлежности точек пересечения сторонам треугольника АВС, находим горизонтальную проекцию линии пересечения треугольников. Способом конкурирующих точек определяем видимость элементов треугольников на горизонтальной плоскости проекций.

Рис. 1.63 Рис. 1.64

горизонтальным следом. Фронтальную проекцию линии пересечения данных плоскостей находим из условия принадлежности точек элемента (сторонам) плоскости общего положения.

В случае задания плоскостей общего положения не следами, то для получения линии пересечения плоскостей последовательно находится точка встречи стороны одного треугольника с плоскостью другого треугольника. Если плоскости общего положения заданы не треугольниками, то линию ппересечения таких плоскостей можно найти путем введения поочередно двух вспомогательных секущих плоскостей – проецирующих (для задания плоскостей треугольниками) или уровня для всех других случаев.

Пересечение прямой общего положения с плоскость общего положения.Ранее были рассмотрены случаи пересечения плоскостей, когда одна из них являлась проецирующей. На основе этого мы можем найти точку пересечения прямой общего положения с плоскостью общего положения, путем введения дополнительной проецирующей плоскости-посредника.

Прежде чем рассматривать пересечение плоскостей общего положения, рассмотрим пересечение прямой общего положения с плоскостью общего положения.

Для нахождения точки встречи прямой общего положения с плоскостью общего положения необходимо:

1) прямую заключить во вспомогательную проецирующую плоскость,

2) найти линию пересечения заданной и вспомогательных плоскостей,

определить общую точку, принадлежащую одновременно двум плоскостям (это их линия пересечения) и прямой.

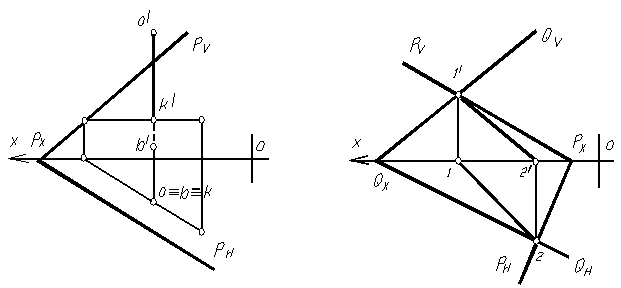
Рис. 1.67 Рис. 1.68

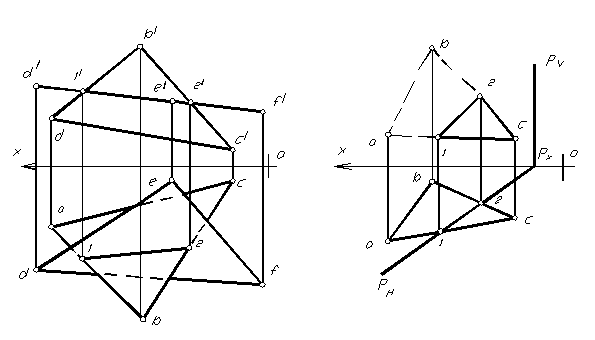
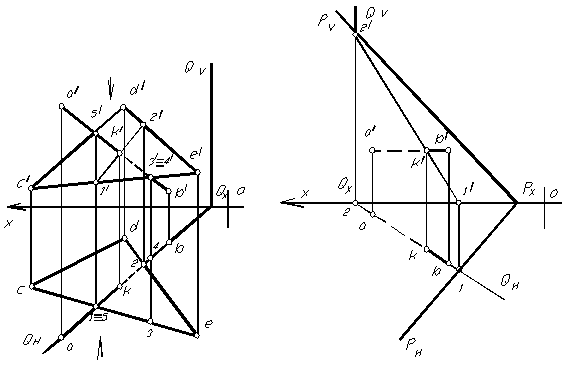
На рисунке 1.66 показан пример нахождения точки встречи прямой АВ, являющейся горизонталью (прямая параллельна горизонтальной плоскости проекций) и плоскости Р, общего положения, заданной следами. Для нахождения точки их пересечения, прямая АВ заключается в горизонтально- проецирующую плоскость Q. Далее поступают, как и в выше изложенном примере.

Для нахождения точки встречи горизонтально-проецирующей прямой АВ с плоскостью общего положения (рис. 1.67 ), через точку встречи прямой с плоскостью (ее горизонтальная проекция совпадает с горизонтальной проекцией самой прямой) проводим горизонталь (т.е. привязываем точку пересечения прямой с плоскостью в плоскость Р). Найдя фронтальную проекцию проведенной горизонтали в плоскости Р, отмечаем фронтальную проекцию точки встречи прямой АВ с плоскостью Р.

Для нахождения линии пересечения плоскостей общего положения, заданных следами достаточно отметить две общие точки, одновременно принадлежащие обеим плоскостям. Такими точками являются точки пересечения их следов (рис.1.68).

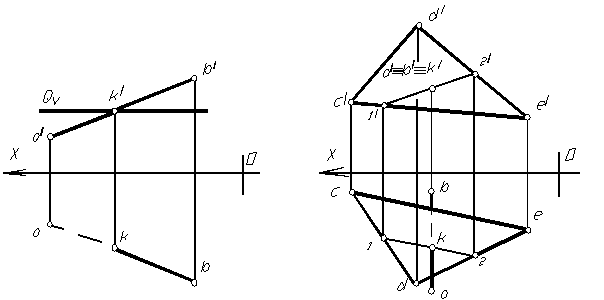
Для нахождения линии пересечения плоскостей общего положения, заданных двумя треугольниками (рис. 1.69), последовательно находим точку

встречи стороны одного треугольника с плоскостью другого треугольника. Взяв любые две стороны из любого треугольника, заключив их в проецирующие плоскости посредники, находятся две точки, одновременно принадлежащие обоим треугольникам – линия их пересечения.

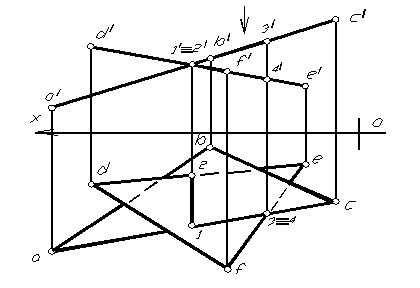
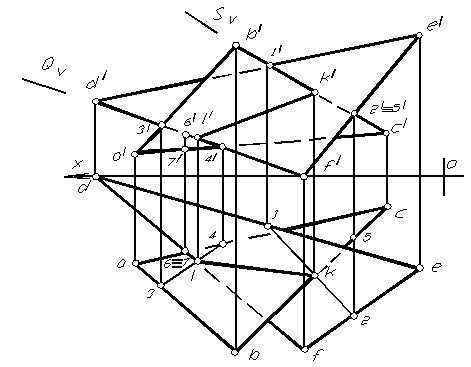
На рисунке 1.69 дан комплексный чертеж треугольников ABC и DEF общего положения. Для нахождения линии пересечения данных плоскостей:

1. Заключаем сторону ВС треугольника АВС во фронтально- проецирующую плоскость S (выбор плоскостей совершенно произвольный).

3. Отмечаем горизонтальную проекцию точки встречи (общая точка двух треугольников) К из пересечения 12 и ВС и находим ее фронтальную проекцию на фронтальной проекции прямой ВС.

4. Проводим вторую вспомогательную проецирующую плоскость Q через сторону DF треугольника DEF.

5. Находим линию пересечения плоскости Q и треугольника АВС – 3 4.

6. Отмечаем горизонтальную проекцию точки L, являющейся точкой встречи стороны DF c плоскостью треугольника АВС и находим ее фронтальную проекцию.

7. Соединяем одноименные проекции точек К и L. К L – линя пересечения плоскостей общего положения, заданных треугольниками АВС и DEF.

8. Способом конкурирующих точек определяем видимость элементов треугольников на плоскостях проекций.

Параллельные плоскости.Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

На рисунке 1.70 построена плоскость, проходящая через точку К параллельная плоскости, заданной пересекающимися прямыми АВ и АС.

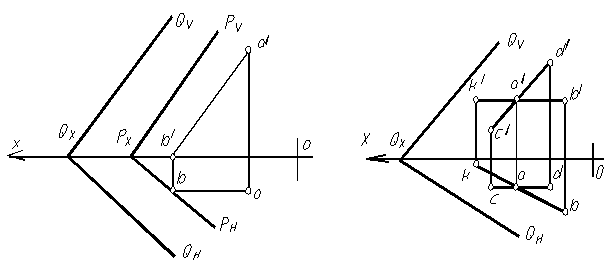Так как выше изложенное действительно и для главных линий параллельных плоскостей, то можно сказать, что плоскости параллельны, если параллельны их одноименные следы (рис. 1.71).

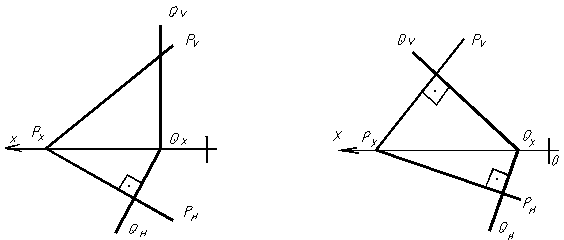Взаимно-перпендикулярные плоскости.Если одна плоскость содержит

хотя бы одну прямую, перпендикулярную другой плоскости, то такие

плоскости перпендикулярны. На рисунке 1.73показаны взаимно перпендикулярные плоскости. На рисунке 1.74 показано построение плоскости, перпендикулярной заданной через точку А, используя условие перпендикулярности прямой (в данном случае главных линий) плоскости.

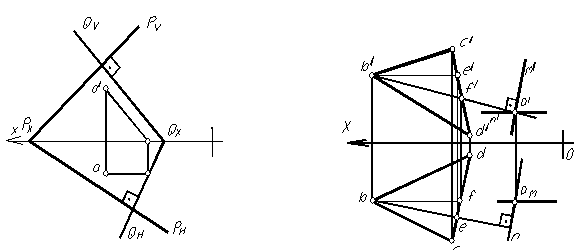Во втором случае в плоскости треугольника проведены горизонталь ВЕ и фронталь BF и через заданную точку А задаем плоскость пересекающимися прямыми (главными линиями), перпендикулярную плоскости треугольника. Для этого проводим через точку А горизонталь и фронталь. Горизонтальную проекцию горизонтали искомой плоскости (N ) проводим перпендикулярно горизонтальной проекции горизонтали треугольника, фронтальную проекцию фронтали новой плоскости (M) – перпендикулярно фронтальной проекции фронтали треугольника.

Источник