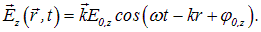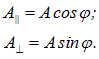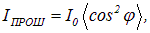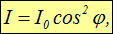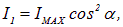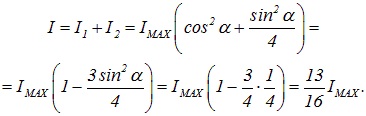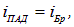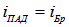Что такое плоскости поляризации и колебаний

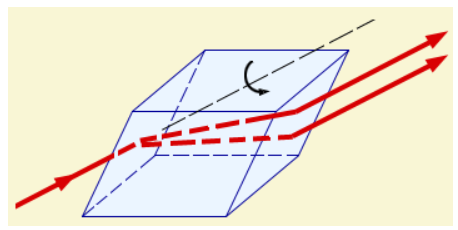
Плоскость поляризации

Смотреть что такое «Плоскость поляризации» в других словарях:

ПЛОСКОСТЬ ПОЛЯРИЗАЦИИ — плоскость, проходящая через направление колебаний электрич. вектора линейно поляризованной световой волны (см. ПОЛЯРИЗАЦИЯ СВЕТА) и направление распространения этой волны. Физический энциклопедический словарь. М.: Советская энциклопедия. Главный… … Физическая энциклопедия

плоскость поляризации — Плоскость, проходящая через направление распространения линейно поляризованного оптического излучения и направление его электрического вектора. [ГОСТ 23778 79] Тематики оптика, оптические приборы и измерения EN plane of polarization DE… … Справочник технического переводчика

плоскость поляризации — 3.4 плоскость поляризации: Плоскость, проходящая через электрический вектор и направление распространения электромагнитной волны. Источник: ГОСТ Р 8.710 2010: Государственная система обеспечения единства измерений. Поляриметры и сахари … Словарь-справочник терминов нормативно-технической документации

плоскость поляризации — poliarizacijos plokštuma statusas T sritis Standartizacija ir metrologija apibrėžtis Plokštuma, išvesta per plokščiai poliarizuotos elektromagnetinės bangos sklidimo kryptį ir elektrinio vektoriaus virpėjimo kryptį. atitikmenys: angl. plane of… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

плоскость поляризации — poliarizacijos plokštuma statusas T sritis Standartizacija ir metrologija apibrėžtis Plokštuma, statmena tiesiai poliarizuotos šviesos elektrinio lauko stiprio vektoriaus virpesių krypčiai. atitikmenys: angl. plane of polarization; polarization… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

плоскость поляризации — poliarizacijos plokštuma statusas T sritis chemija apibrėžtis Plokštuma, statmena tiesiškai poliarizuotos šviesos elektrinio lauko stiprio vektoriaus virpesių krypčiai. atitikmenys: angl. polarization plane rus. плоскость поляризации … Chemijos terminų aiškinamasis žodynas

плоскость поляризации — poliarizacijos plokštuma statusas T sritis fizika atitikmenys: angl. plane of polarization vok. Polarisationsebene, f rus. плоскость поляризации, f pranc. plan de polarisation, m … Fizikos terminų žodynas

ПЛОСКОСТЬ ПОЛЯРИЗАЦИИ — плоскость, проходящая через направление распространения и направление колебаний электрич. вектора в линейно поляризов. электромагнитной волне (см. Поляризация волн, Поляризация света). Прежде эту плоскость наз. плоскостью колебаний, а под П. п.… … Большой энциклопедический политехнический словарь

плоскость поляризации радиоволны — плоскость поляризации Плоскость, в которой лежат вектор напряженности электрического поля и направление распространения радиоволны. [ГОСТ 24375 80] Тематики радиосвязь Обобщающие термины распространение радиоволн Синонимы плоскость поляризации … Справочник технического переводчика

Плоскость поляризации радиоволны — 36. Плоскость поляризации радиоволны Плоскость поляризации Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Источник

Поляризация света

Начало XIX века для физики ознаменовалось развитием волновой теории света, которым занимались ученые Т. Юнг и О. Френель. В то время природа световых волн оставалась неизвестной. Изначально предполагалось, что свет является распространяющимися в некоторой гипотетической среде – эфире продольными волнами. Однако в процессе изучения явлений дифракции и интерференции вопрос о том, продольные или поперечные световые волны, стал второстепенен. На тот момент казалось невозможным, что свет – это поперечные волны, по той причине, что по аналогии с механическими волнами пришлось бы признать эфир твердым телом, ведь поперечные механические волны не обладают возможностью распространяться в газообразной или же жидкой среде.

Несмотря ни на что, постепенно копились свидетельствующие в пользу поперечности световых волн экспериментально полученные факты.

Поляризация света

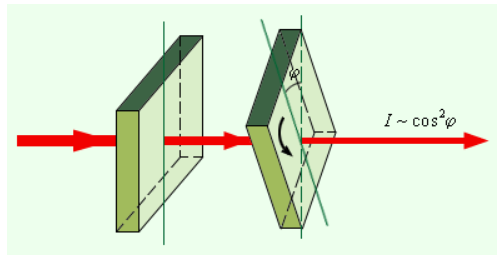
Как же получить поляризованный свет?

Интенсивность прошедшего света оказалась прямо пропорциональной cos 2 φ :

Двойное лучепреломление точно также, как и закон Малюса не может быть объяснено с точки зрения теории продольных волн. Для продольных волн направление распространения луча представляет собой ось симметрии. В них любые направления в плоскости, нормальной, то есть перпендикулярной, лучу, равноправны.

Выходит, что асимметрия относительно направления распространения луча – это решающий признак, отличающий поперечную и продольную волны. Первым высказал догадку о поперечности световых волн Т. Юнг в 1816 году. Независимо от Юнга Френель тоже выдвинул концепцию поперечности световых волн, и даже смог обосновать ее с помощью большого количества опытов. Им была создана теория двойного лучепреломления света в кристаллах.

Пропала необходимость во введении особой среды распространения волн – эфира, который приходилось рассматривать как твердое тело. Благодаря этому электромагнитная теория света приобрела должную стройность.

В каждом из процессов взаимодействия света с веществом электрический вектор E → играет основную роль. По данной причине его называют световым вектором.

Виды поляризации света

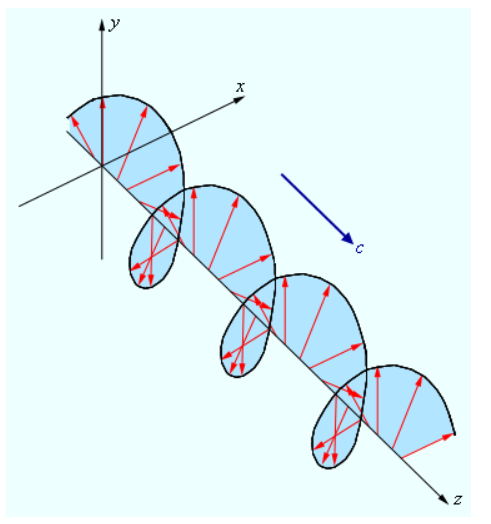
Если при распространении электромагнитной волны световой вектор сохраняет свою ориентацию, то подобная волна носит название линейно поляризованной или плоско поляризованной. Отметим, что термин поляризации волн ввел Малюс применительно к поперечным механическим волнам.

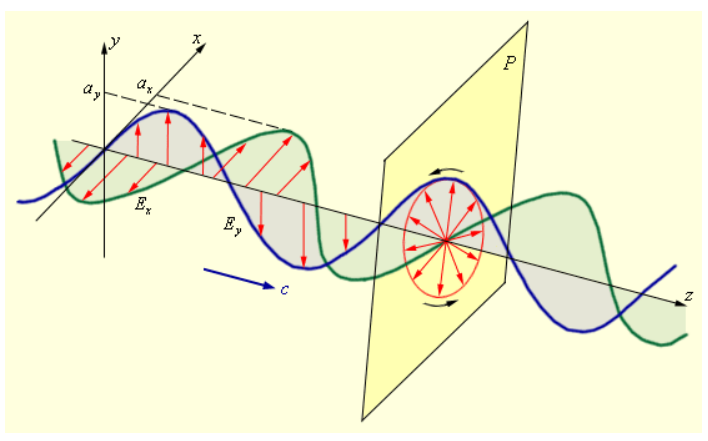
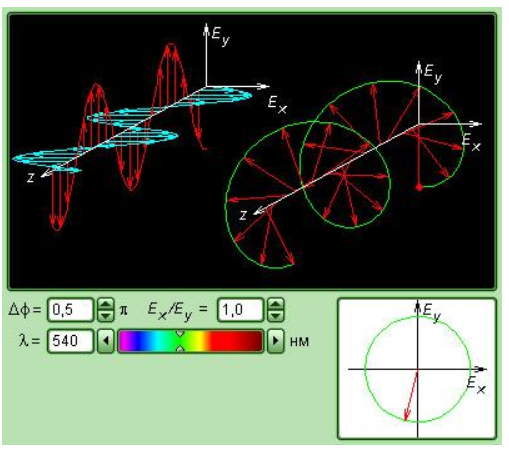
В нормальной (то есть перпендикулярной) направлению распространения волны эллиптически поляризованной волне в каждой плоскости P конец результирующего вектора E → за период светового колебания обходит некоторый эллипс, носящий название эллипса поляризации.

Его размер и форма характеризуются амплитудами a x и a y линейно поляризованных волн и фазовым сдвигом Δ φ между ними.

Линейно поляризованный свет производится лазерными источниками. В случае отражения или рассеяния свет может стать поляризованным. В частности, голубой свет от неба частично или полностью поляризован. Однако, свет, который испускают обычные источники, такие как, например, солнечный свет и излучение ламп накаливания, является неполяризованным. Свет, исходящий от подобных источников, в любой момент состоит из вкладов огромного числа независимо излучающих атомов, обладающими различной ориентацией светового вектора в волнах, которые они излучают. По этой причине в результирующей волне вектор E → хаотично меняет свою ориентацию во времени, из-за чего в среднем все направления колебаний получаются равноправными.

Неполяризованный свет также называют естественным светом.

Кристаллы, в которых происходит двойное лучепреломление, называются анизотропными.

У значительной части кристаллов поглощение света кардинально зависимо от направления электрического вектора в световой волне. Такое явление носит название дихроизма.

В частности, данным свойством обладают использованные в знакомых нам опытах Малюса пластины турмалина. При некоторой толщине пластинка турмалина практически полностью поглощает одну из взаимно перпендикулярно поляризованных волн (как, к примеру, E x ) и частично пропускает вторую волну (то есть E y ).

Направление колебаний электрического вектора в прошедшей волне является разрешенным направлением пластины.

Пластинка турмалина может применяться как для создания поляризационного света, то есть в качестве поляризатора, так и для анализа характера поляризации света, как анализатор.

В наше время часто применяются искусственные дихроичные пленки, называющиеся поляроидами.

Поляроиды пропускают практически всю волну разрешенной поляризации и не пропускают поляризованную в нормальном направлении волну. Исходя из всего вышесказанного, можно заявить, что поляроиды – это идеальные поляризационные фильтры.

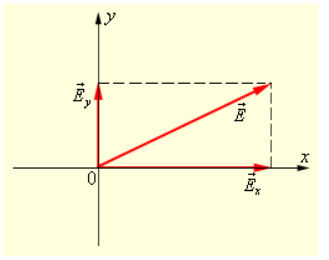
Выходит, что в электромагнитной теории света закон Малюса находит естественное объяснение, чья основа заключается в разложении вектора E → на его составляющие.

Источник

6.1. Поляризация света

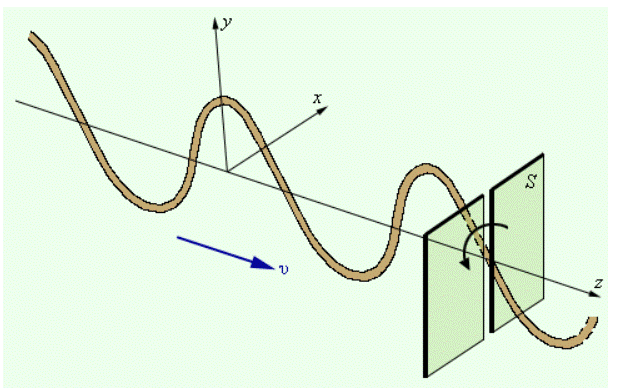
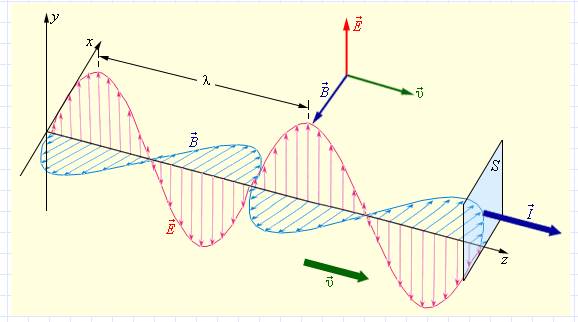
Следствием теории Максвелла является поперечность электромагнитных (световых) волн распространяющихся в вакууме или изотропной среде: векторы напряженности электрического и магнитного полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости v распространения волны (то есть перпендикулярно световому лучу). Явление поляризации света служит надежным обоснованием поперечности световой волны. При рассмотрении поляризации обычно все рассуждения связывают с плоскостью колебаний вектора напряженности электрического поля Е — светового вектора, так как химическое, физиологическое и другие виды воздействия света на вещество обусловлены главным образом электрическими колебаниями. Однако при этом следует помнить об обязательном существовании перпендикулярного ему вектора напряженности магнитного поля Н.

Поляризация электромагнитной волны. Записывая решение для электрического поля плоской электромагнитной волны в виде

мы предполагали, что направление вектора амплитуды колебаний не зависит от времени. В этом случае вектор электрического поля всегда и во всех точках волны направлен вдоль одной и той же прямой — колеблется в одной плоскости неизменной ориентации в пространстве.

Плоскость, в которой происходят колебания светового вектора, то есть плоскость, содержащая вектор 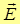и направление распространения волны, называется плоскостью колебаний. Если эта плоскость не меняет во времени своей ориентации, то волна называется — линейно (плоско) поляризованной.

Выбирая ось х вдоль направления распространения волны, а ось у — вдоль векторной амплитуды 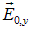, записываем (6.1) в виде

Однако существует и вторая линейно поляризованная волна, имеющая ту же частоту и распространяющаяся в том же направлении:

Электрические колебания в этой волне направлены вдоль оси z, так что волны (6.2) и (6.3) линейно независимы. Обе они являются решением одного и того же волнового уравнения, так что их суперпозиция также является решением того же уравнения. Сложив эти волны, мы найдем общее выражение для монохроматической волны с данной частотой w, распространяющейся вдоль оси х. Математически эта процедура ничем не отличается от сложения взаимно ортогональных колебаний. Если зафиксировать какую-то точку х и следить за изменением вектора электрического поля в ней, то конец вектора будет описывать эллиптическую, в общем случае, траекторию в плоскости, параллельной y0z. Вращение вектора происходит с частотой волны . В этом случае говорят, что свет имеет эллиптическую поляризацию. Если разность фаз кратна , то эллиптическая поляризация вырождается в линейную. При равенстве амплитуд Е_0,у и Е_0,г эллипс превращается в окружность. Тогда говорят о круговой поляризации волны. В соответствии с двумя возможными направлениями вращения вектора возможны право- и левополяризованные волны. Любую электромагнитную волну можно представить как линейную комбинацию двух линейно поляризованных волн или как линейную комбинацию двух волн с круговой поляризацией. Иными словами, электромагнитные волны имеют две внутренние степени свободы.

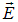
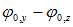
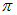
Естественный и поляризованный свет. В свете, испускаемом обычными источниками, имеются колебания, совершающиеся в различных направлениях, перпендикулярных к лучу. В таких световых волнах, исходящих из различных элементарных излучателей (атомов), векторы имеют различные ориентации, причем все эти ориентации равновероятны, что обусловлено большим числом атомных излучателей. Такой свет называется естественным, или неполяризованным.

Если под влиянием внешних воздействий на свет или внутренних особенностей источника света (лазер) появляется предпочтительное, наиболее вероятное направление колебаний, то такой свет называется частично поляризованным. Неполяризованный (естественный) свет может испускаться лишь огромным числом элементарных излучателей. Электромагнитная волна от отдельного элементарного излучателя (атома, молекулы) всегда поляризована. С помощью различных поляризаторов из пучка естественного света можно выделить часть, в которой колебания вектора 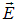будут происходить в одном определенном направлении в плоскости, перпендикулярной лучу, то есть выделенный свет будет линейно поляризованным.

На рисунках направление колебаний электрического поля линейно поляризованной волны изображается следующим образом. Если вектор Е колеблется в плоскости чертежа, то на направление вектора скорости волны 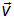наносится ряд вертикальных стрелочек (рис. 6.1-1), а если в плоскости, перпендикулярной чертежу, — ряд точек (рис. 6.1-2). Естественный (неполяризованный) свет условно обозначается чередующимися черточками, которым соответствует, например, компонента Е_y вектора напряженности электрического поля, и точками, соответствующими другой компоненте Е_z (рис. 6.1-3).

Рис. 6.1. Условные обозначения типа поляризации волны

Существуют приборы (поляризаторы), пропускающие только колебания, происходящие параллельно некоторой плоскости, называемой плоскостью поляризации прибора, и полностью задерживающие ортогональные колебания. Если пропустить через такой прибор пучок света, то на выходе он будет линейно поляризованным. При вращении прибора вокруг направления луча интенсивность выходящего света будет изменяться от I_MAX до I_MIN.

Степень поляризации света — это величина

Отметим, что формула (6.4) пригодна для расчета степени поляризации света лишь в том случае, когда частично поляризованный свет представляет собой смесь естественного света и света линейно поляризованного и не работает, например, в случае смеси естественного света и света поляризованного по кругу. В общем случае степень поляризации может быть рассчитана как отношение интенсивности поляризованной компоненты к суммарной интенсивности волны, то есть сумме интенсивностей поляризованной и естественной компонент смеси:

Нетрудно показать, что (6.4) есть частный случай последней формулы.

Если падающий пучок света линейно поляризован, то при положении прибора, когда его плоскость поляризации ортогональна плоскости колебаний волны, свет через прибор не пройдет, то есть . В соответствии с формулой (6.4) степень поляризации такого света . Для частично поляризованного света

и . Для естественного света, где волны разных поляризаций смешаны в равной степени и все направления эквивалентны, интенсивность выходящего света не изменяется при вращении поляризатора, так что и .

Закон Малюса. В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора Е, например природные кристаллы турмалина. Монокристалл турмалина поглощает колебания вектора Е в одном направлении настолько сильно, что сквозь пластинку толщиной порядка 1 мм проходит только линейно поляризованный луч. Кристаллы йодистого хинина еще сильнее поглощают одну из поляризаций: кристаллическая пленка толщиной в десятую долю миллиметра практически полностью отделяет один из линейно поляризованных лучей.

Пусть естественный свет распространяется перпендикулярно плоскости рисунка 6.2.

Рис. 6.2. Разложение вектора амплитуды колебаний А в волне, падающей на поляризатор

Вектор амплитуды колебаний электрического поля волны, совершающихся в плоскости, образующей с плоскостью поляризатора угол , можно разложить на два колебания с амплитудами

Первое колебание с амплитудой А_|| пройдет через прибор (поляризатор), второе — с амплитудой А — будет задержано (поглощено). Интенсивность прошедшей волны пропорциональна квадрату амплитуды

Падающая волна является смесью волн с различными углами . Усредняя по углам, получаем для интенсивности света на выходе из поляризатора:

где — интенсивность падающего на поляризатор света. В естественном свете все значения угла равновероятны:

так что интенсивность света, прошедшего через поляризатор, будет равна . При вращении поляризатора вокруг направления луча естественного света интенсивность прошедшего света остается неизменной, но изменяется лишь ориентация плоскости колебаний света, выходящего из прибора.

Рассмотрим теперь падение линейно поляризованного света с интенсивностью на тот же поляризатор (рис. 6.3).

Рис. 6.3. Прохождение линейно поляризованной волны через поляризатор

Сквозь прибор пройдет составляющая колебаний с амплитудой

где — угол между плоскостью колебаний вектора Е и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением

которое носит название закона Малюса.

Поляризационные приборы по своему целевому назначению делятся на поляризаторы и анализаторы. Поляризаторы служат для получения поляризованного света. С помощью анализатора можно убедиться, что падающий свет поляризован, и выяснить направление плоскости поляризации. Принципиальных различий в конструкционном отношении между поляризатором и анализатором не существует.

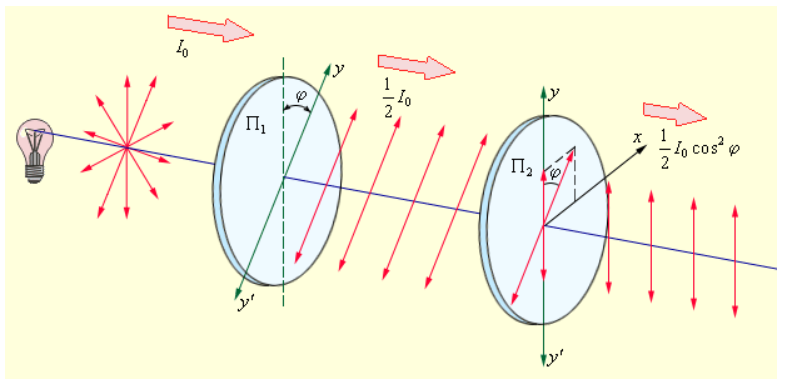
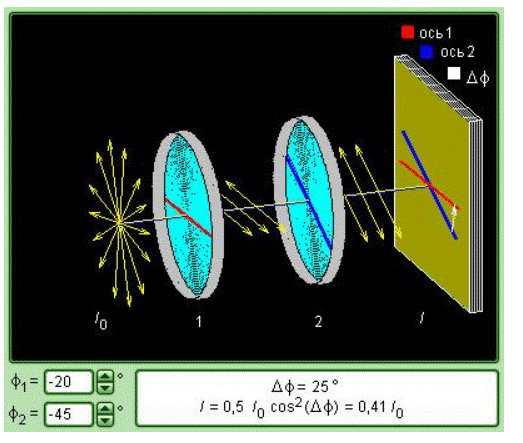
Поставим на пути естественного света два поляризатора, плоскости которых образуют угол (рис. 6.4).

Рис. 6.4. Пропускание естественного света через систему из двух поляризаторов

Из первого поляризатора выйдет линейно поляризованный свет, интенсивность которого , составит половину интенсивности падающего естественного света . Согласно закону Малюса из второго поляризатора (который играет роль анализатора) выйдет свет с интенсивностью

Таким образом, интенсивность света, прошедшего через два поляризатора, равна

Если угол (плоскости поляризации поляризатора и анализатора параллельны), то ; если (анализатор и поляризатор скрещены), то .

Пример 1. В частично поляризованном свете амплитуда колебаний, соответствующая максимальной интенсивности света при прохождении через поляризатор, в n = 2 раза больше амплитуды, соответствующей минимальной интенсивности. Определим степень поляризации света.

Поскольку интенсивность пропорциональна квадрату амплитуды, имеем

Отсюда степень поляризации света равна

Пример 2. На пути света со степенью поляризации Р = 0.6 поставили анализатор так, что интенсивность прошедшего света стала максимальной. Определим, во сколько раз уменьшится интенсивность, если анализатор повернуть на угол ?

В падающем луче по условию (см. предыдущий пример)

При повороте анализатора на угол будут пропущены колебания, параллельные плоскости поляризации прибора. Поэтому интенсивность пропущенных колебаний, прежде бывших параллельными плоскости поляризации, составит

a интенсивность прошедших колебаний, до поворота задерживавшихся анализатором, равна

Суммарная интенсивность прошедших колебаний равна сумме

Стало быть, интенсивность уменьшится при повороте анализатора в 16/13 = 1.23 раза.

Рис. 6.5. Поляризация света при отражении и преломлении

Степень поляризации зависит от угла падения лучей и от относительного показателя преломления сред. Исследуя это явление, английский физик Д. Брюстер установил, что при определенном значении угла падения

отраженный свет полностью поляризован в плоскости, перпендикулярной плоскости падения луча. Это соотношение известно как закон Брюстера. При

отражается только та компонента вектора напряженности электрического поля, которая параллельна поверхности диэлектрика (перпендикулярна плоскости падения). Соответственно, преломленный луч всегда частично поляризован, так как отражается лишь какая-то доля падающего света (не равная 50 %).

При падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны, отраженный свет полностью поляризован в плоскости, перпендикулярной плоскости падения луча, а преломленный луч частично поляризован с максимальной степенью поляризации.

находим с учетом закона преломления

откуда следует, что преломленный луч 0С перпендикулярен отраженному лучу 0В (рис. 6.6).

Рис.6.6. Ход лучей при падении света под углом Брюстера: отраженный луч ортогонален преломленному,
поэтому излучатели типа (см. текст ниже) не вносят вклад в поляризацию отраженного луча

Для того чтобы объяснить, почему отраженный при падении под углом Брюстера луч линейно поляризован в плоскости, перпендикулярной плоскости падения, учтем, что отраженный свет есть результат излучения вторичных волн колеблющимися под действием светового вектора волны электрическими зарядами (электронами) в среде II. Эти колебания происходят в направлении колебаний вектора Е.

Разложим колебания вектора Е в среде II на два взаимно перпендикулярных направления (см. рис. 6.6): колебания , происходящие в плоскости падения (показаны стрелками), и колебания , происходящие перпендикулярно плоскости падения (показаны точками). В случае падения под углом Брюстера

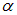
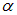
отраженный луч 0В перпендикулярен преломленному лучу 0С. Следовательно, 0В параллелен . Из электромагнитной теории Максвелла известно, что колеблющийся электрический заряд не излучает электромагнитных волн вдоль направления своего движения. Поэтому колеблющийся в диэлектрике излучатель типа вдоль направления 0В не излучает. Таким образом, по направлению отраженного луча 0В распространяется свет, посылаемый только излучателями типа , направления колебаний которых перпендикулярны плоскости падения.

Следует отметить, что на опыте закон Брюстера не выполняется вполне строго из-за дисперсии света.

Пример 3. Определим, на какой угловой высоте над горизонтом должно находиться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован.

Угол падения света связан с высотой Солнца над горизонтом соотношением

По условию угол падения равен углу Брюстера, так что

Показатели преломления воды п₂ = 1.33, воздуха — п₁ = 1. Отсюда находим

Пример 4. Угол Брюстера при падении света из воздуха на кристалл каменной соли равен . Определим скорость света V в этом кристалле.

Поскольку показатель преломления воздуха равен единице, показатель преломления каменной соли п совпадает с относительным показателем преломления этих двух сред. Имеем поэтому

Источник