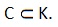Что такое подмножество 6 класс
Множества
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
Подмножество — это множество, все элементы которого, являются частью другого множества.
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :
Рассмотрим два множества:
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
При объединении равных множеств объединение будет равно любому из данных множеств:
6.1.6. Множество и его элементы
I. Множество представляет собой совокупность некоторых предметов или чисел, составленных по каким-либо общим свойствам или законам (множество букв на странице, множество правильных дробей со знаменателем 5, множество звезд на небе и т.д.).
Для записи множества используют фигурные скобки: « <»- множество открывается; «>» — множество закрывается. А само множество называют заглавными латинскими буквами: А, В, С и так далее.
Примеры.
1. Записать множество А, состоящее из всех гласных букв в слове «математика».
Решение. А=<а, е, и>. Вы видите: несмотря на то,что в слове «математика» имеется три буквы «а» — в записи множества повторений не допускается, и буква «а» записывается только один раз. Множество А состоит из трех элементов.
2. Записать множество всех правильных дробей со знаменателем 5.
Решение. Вспоминаем: правильной называют обыкновенную дробь, у которой числитель меньше знаменателя. Обозначим через В искомое множество. Тогда:
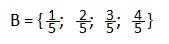
II. Множества состоят из элементов и бывают конечными или бесконечными. Множество, которое не содержит ни одного элемента, называют пустым множеством и обозначают Ø.
III. Множество В называют подмножеством множества А, если все элементы множества В являются элементами множества А.
3. Какое из двух данных множеств В и С является подмножеством множества К,
Решение. Все элементы множества С являются также элементами множества К, поэтому, множество С является подмножеством множества К. Записывают:
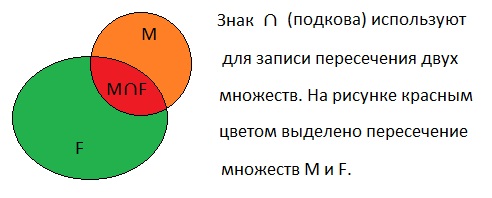
IV. Пересечением множеств А и В называется множество, элементы которого принадлежат и множеству А и множеству В.
4. Показать пересечение двух множеств М и F с помощью кругов Эйлера.
Решение.
V. Объединением множеств А и В называется множество, элементы которого принадлежат хотя бы одному из данных множеств А и В.
5. Показать с помощью кругов Эйлера объединение множеств Т и Р.
Множество и его элементы. Подмножества
Понятие множества
Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».
Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».
Приведём примеры множеств:
Множество людей в салоне самолёта
Множество деревьев в парке
Множество планет Солнечной системы
Множество электронов в атоме
Множество натуральных чисел
Множество «синих-синих презелёных красных шаров»
Конечное, бесконечное и пустое множества
Людей в салоне самолёта легко посчитать, это множество конечно.
С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.
Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.
Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.
Помидоры на грядке
Числа (натуральные, рациональные, действительные и т.д.)
Количество рациональных чисел на отрезке [0;1]
Полосатые летающие слоны
Все точки пересечения двух параллельных прямых на плоскости
Способы задания множеств
1) Перечисление – в списке задаются все элементы множества.
Множество всех континентов Земли:
Множество букв слова «математика»:
Множество натуральных чисел меньших 5:
2) Характеристическое свойство – указывается особенность элементов множества.
D =
3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)
Подмножества
Говорят, что B содержит A, или B покрывает A.
Пустое множество является подмножеством любого множества.
Множество людей является подмножеством приматов, живущих на Земле.
Множество квадратов является подмножеством прямоугольников.
Множество всех подмножеств данного множества A называют булеаном или степенью множества A.
Примеры
Пример 1. Запишите данное множество с помощью перечисления элементов:
Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:
Задано множество целых чисел, модуль которых не больше 3. Перечисляем:
Задано множество рациональных чисел, являющихся корнями уравнения
(x-1)(2x+5) = 0. Перечисляем:
Пример 2. Запишите данное множество с помощью характеристического свойства:
а) Множество всех натуральных чисел меньше 10
б) Множество всех действительных чисел, кроме 0
в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1
Пример 3. Изобразите на графике в координатной плоскости данное множество:
Задано конечное множество точек, которое можно представить перечислением:
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:
Словари
Под множеством понимается совокупность каких-либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов. Терминология и многие результаты этой теории широко используются в математике, например в математическом анализе, геометрии и теории вероятностей.
Сравнение множеств. Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие. Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств. Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их столицами, хотя можем оставаться в неведении относительно общего их числа. Мы могли бы утверждать: «Столиц штатов ровно столько, сколько штатов». Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В теории множеств аналогичные утверждения используются, даже когда множества содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из первого множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе, или, что первое множество имеет большую мощность. С понятием мощности связаны, казалось бы, удивительные результаты. Например, на первый взгляд положительных целых чисел в два раза больше, чем четных положительных чисел, так как четно каждое второе число. Но, согласно теории множеств, четных положительных чисел столько же, сколько всех положительных целых чисел. Действительно, можно образовать пары чисел 2 и 1, 4 и 2, 6 и 3 и, вообще каждому четному числу 2n поставить в соответствие целое число n. Именно это обстоятельство имел в виду Б. Рассел (1872-1970), сформулировав факт, названный им парадоксом Тристрама Шенди. Герой романа Стерна сетовал на то, что ему потребовался целый год, чтобы изложить события первого дня его жизни, еще один год понадобился, чтобы описать второй день, и что при таком темпе он никогда не завершит свое жизнеописание. Рассел возразил, заметив, что если бы Тристрам Шенди жил вечно, то смог бы закончить свое жизнеописание, так как события n-го дня Шенди мог бы описать за n-й год и, таким образом, в летописи его жизни ни один день не остался бы не запечатленным. Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней. Эти примеры показывают, что бесконечное множество можно поставить во взаимно однозначное соответствие со своим бесконечным подмножеством. Иногда это свойство принимают за определение бесконечного. Если можно установить взаимно однозначное соответствие между некоторым множеством и множеством положительных целых чисел, то говорят, что такое множество счетно. Для обозначения количества элементов в счетном множестве часто используют символ А0 (алеф-нуль). Так называемые «трансфинитные» числа, например А0, могут не подчиняться обычным законам арифметики. Например, так как существует А0 четных чисел, А0 нечетных и А0 целых чисел, то приходится признать, что А0 + А0 = А0. Идея сравнения множеств путем установления взаимно однозначного соответствия между ними используется в различных разделах математики. Число всех действительных чисел, как показал основатель научной теории множеств Г. Кантор (1845-1918), больше, чем А0 чисел. Следовательно, если можно показать, что множество действительных чисел, обладающих некоторым особым свойством, является всего лишь счетным множеством, то заведомо должны существовать действительные числа, этим свойством не обладающие. Например, так как множество алгебраических чисел счетно, должны существовать неалгебраические числа. Такие числа называются трансцендентными. Поразительная и далеко не очевидная теорема, высказанная в качестве гипотезы Кантором и доказанная Э. Шредером и Ф. Бернштейном около 1896, утверждает, что если можно установить взаимно однозначное соответствие между множеством A и подмножеством множества B, и между множеством B и подмножеством множества A, то существует взаимно однозначное соответствие между всем множеством A и всем множеством B.
Аксиома выбора. Неожиданные трудности в теории множеств могут возникнуть, казалось бы, в самых простых случаях. Если, например, задано семейство непересекающихся множеств, ни одно из которых не пусто, то интуитивно кажется очевидным, что мы можем построить новое множество, содержащее ровно по одному элементу из каждого множества, входящего в это семейство. Но если наше семейство содержит бесконечно много множеств, то для построения нового множества может потребоваться бесконечное число произвольных выборов, а законность такого процесса при тщательном анализе становится отнюдь не очевидной. Аксиома выбора, утверждающая, что такое множество существует, была впервые сформулирована в 1904 Э. Цермело (1871-1953). До сих пор не удалось показать, что аксиома выбора следует из остальных аксиом теории множеств. Но около 1938 К.Гедель (1906-1978) показал, что если теория множеств непротиворечива (т.е. не содержит внутренних противоречий) без аксиомы выбора, то она остается непротиворечивой и после присоединения к ней аксиомы выбора.
Куратовский К., Мостовский А. Теория множеств. М., 1970
Подмножество
Смотреть что такое «Подмножество» в других словарях:
подмножество — совокупность; множество Словарь русских синонимов. подмножество сущ., кол во синонимов: 1 • множество (88) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
ПОДМНОЖЕСТВО — нем. Teilgesamtheit. Множество, каждый элемент к рого является элементом другого множества. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Подмножество — [subset] см. Множество … Экономико-математический словарь
подмножество — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4609] Тематики защита информации EN subset … Справочник технического переводчика
Подмножество — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
подмножество — а; ср. Матем. Множество элементов, каждый из которых принадлежит другому, более крупному, большому множеству. * * * подмножество понятие теории множеств. Подмножество множества А множество В (обозначается ), каждый элемент которого принадлежит А … Энциклопедический словарь
подмножество — ▲ множество ↑ частичный подмножество множество, являющееся частью большего множества. под. (подсистема). подгруппа. | фракция. сочетание целое подмножество (матем). сочетать. ▼ вид ↓ выделять (из прочих) с … Идеографический словарь русского языка
ПОДМНОЖЕСТВО — понятие теории множеств. П. множества А множество В (обозначается В с Л), каждый элемент к рого принадлежит А. Напр., множество всех чётных чисел является П. множества всех целых чисел … Естествознание. Энциклопедический словарь
подмножество — подмн ожество, а … Русский орфографический словарь