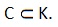Что такое подмножество в математике 6 класс виленкин
6.1.6. Множество и его элементы
I. Множество представляет собой совокупность некоторых предметов или чисел, составленных по каким-либо общим свойствам или законам (множество букв на странице, множество правильных дробей со знаменателем 5, множество звезд на небе и т.д.).
Для записи множества используют фигурные скобки: « <»- множество открывается; «>» — множество закрывается. А само множество называют заглавными латинскими буквами: А, В, С и так далее.
Примеры.
1. Записать множество А, состоящее из всех гласных букв в слове «математика».
Решение. А=<а, е, и>. Вы видите: несмотря на то,что в слове «математика» имеется три буквы «а» — в записи множества повторений не допускается, и буква «а» записывается только один раз. Множество А состоит из трех элементов.
2. Записать множество всех правильных дробей со знаменателем 5.
Решение. Вспоминаем: правильной называют обыкновенную дробь, у которой числитель меньше знаменателя. Обозначим через В искомое множество. Тогда:
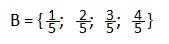
II. Множества состоят из элементов и бывают конечными или бесконечными. Множество, которое не содержит ни одного элемента, называют пустым множеством и обозначают Ø.
III. Множество В называют подмножеством множества А, если все элементы множества В являются элементами множества А.
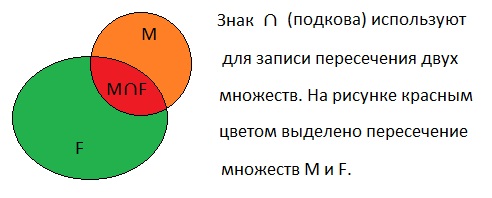
3. Какое из двух данных множеств В и С является подмножеством множества К,
Решение. Все элементы множества С являются также элементами множества К, поэтому, множество С является подмножеством множества К. Записывают:
IV. Пересечением множеств А и В называется множество, элементы которого принадлежат и множеству А и множеству В.
4. Показать пересечение двух множеств М и F с помощью кругов Эйлера.
Решение.
V. Объединением множеств А и В называется множество, элементы которого принадлежат хотя бы одному из данных множеств А и В.
5. Показать с помощью кругов Эйлера объединение множеств Т и Р.
Что такое подмножество в математике 6 класс виленкин
Ключевые слова конспекта: множества, операции над множествами, подмножество, пересечение множеств, объединение множеств, элемент множества, числовые множества, обозначение некоторых числовых множеств.
В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.
В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.
Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.
Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.
Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.
Конечное мнoжество может содержать миллиард элементов, 2 элемента, 1 элемент или даже не содержать ни одного элемента.
Пустое множeство — это мнoжество, не содержащее ни одного элемента. Для обозначения пустого мнoжества ввели специальный знак ∅.
Конечные множeства обычно записывают с помощью фигурных скобок. Например, множество вершин пятиугольника ABCDE можно записать так: , а множество двузначных чисел, кратных 15, так: . В таких случаях говорят, что множество задано перечислением его элементов.
Множeства принято обозначать большими буквами латинского алфавита. Например, рассмотренные выше множества вершин пятиугольника и двузначных чисел, кратных 15, можно обозначить соответственно буквами К и L и записать так: К = <А, В, С, D, Е>; L = <15, 30, 45, 60, 75, 90>.
Для основных числовых множеств введены специальные обозначения: множество натуральных чисел обозначают буквой N (от латинского слова natural — «естественный»), множество целых чисел — буквой Z (от немецкого слова zahl — «число»), множество рациональных чисел — буквой Q (от латинского слова quotient — «отношение»).
В тех случаях, когда задание множества перечислением элементов невозможно (как для бесконечного множества) или громоздко (как для конечного мнoжества с большим числом элементов), множество задают описанием, указав его характеристическое свойство, т. е. свойство, которым обладают все элементы этого множeства и не обладают никакие другие объекты.
Это конспект по математике на тему «Множества. Операции над множествами». Выберите дальнейшие действия:
Урок по математике на тему «Множества»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Тема урока: Множество
и его элементы. Подмножество.
ОБУЧЕНИЯ: формирование умений выделять множества, подмножества; формирование навыков находить на изображениях область пересечения и объединения множеств и называть элементы из этой области, решать задачи;
ВОСПИТАТЕЛЬНЫЕ: культуры умственного труда. Воспитание аккуратности при работе в тетради, самостоятельности, грамотной математической речи
РАЗВИВАЮЩИЕ: Развитие мышления учащихся (в ходе выполнения заданий актуализации и на протяжении всего урока). внимания учащихся (выполнение заданий на нахождение соответствия). Развитие памяти учащихся
ТИП УРОКА: изучение нового материала
1. организационный момент
1) 52 + 32 2)67 – 25 3) 51:10
3. Изучение нового материала
Множество возникает путем объединения
отдельных предметов в единое целое.
Оно есть множественность мыслимая как единое.
Множество представляет собой объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам.
множество компьютеров и т.д.
«Множество есть многое, мыслимое нами как единое»
(основатель теории множеств – Георг Кантор)
Предметы, составляющие данное множество, называются его элементами. Элементы множества букв в слове САМОПОЗНАНИЕ
Э
С

М = 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 множество цифр
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством множества А.
В подмножество множества А
Пустое множество, по определению, считают подмножеством всякого множества.
Если два множества состоят из одних и тех же элементов, то они называются равными.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов.
Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц ( 1646 — 1716 ). Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы. [
Перечислите множество фруктов
Перечислите множество овощей
Перечислите множество школьных предметов учеников 6 класса
Перед вами три круга изображающие круги Эйлера. В самом маленьком круге напишите, те знания и умения которые вы приобрели в дошкольном возрасте (множества А), во втором круге – чем пополнились ваши знания в начальной школе (множества В) и в самом большом круге чему вы научились в 5-6 классах (множество С). В каком отношении находятся эти множества? (ответ А подмножества множества В и в – подмножества множества С)
Множества
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
Подмножество — это множество, все элементы которого, являются частью другого множества.
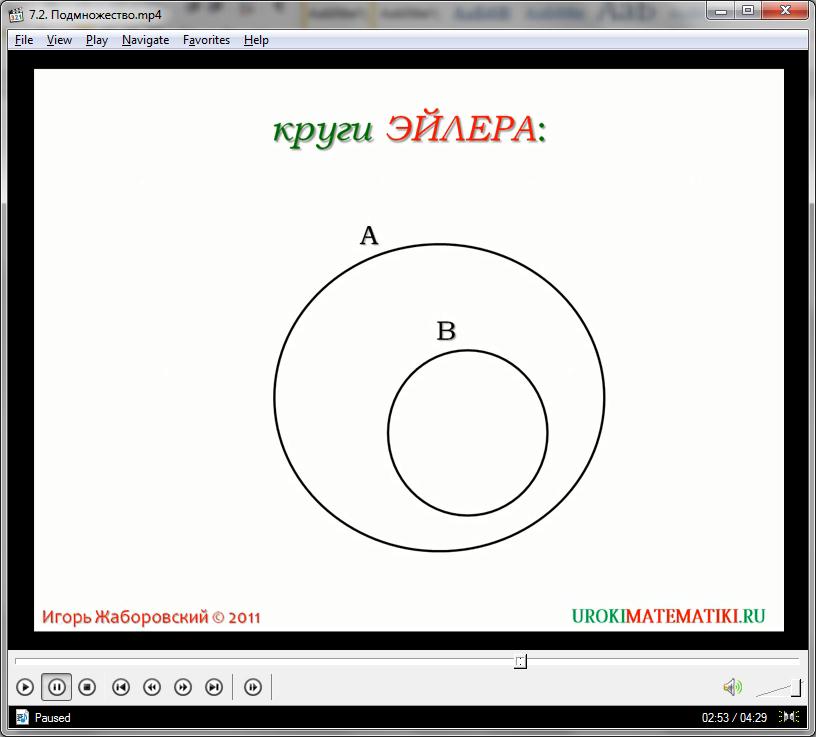
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :
Рассмотрим два множества:
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
При объединении равных множеств объединение будет равно любому из данных множеств:
Урок «Подмножество»
Краткое описание документа:
Как известно, множество является одним из важнейших элементов алгебры, а точнее – теории множеств. Это понятие не имеет строгого определения в силу своей аксиоматичности и фундаментальности, и передается на словах, как некий набор математических реальных чисел. Множества могут быть разными, включать большой спектр различных постоянных и переменных элементов, либо же вообще быть пустыми. Множество всех существующих определяемых чисел является бесконечным математическим множеством. А эфемерное множество, не содержащее никаких значимых объектов, именуется пустым.
В зависимости от свойств объектов, допускается выделение особых групп внутри множества. Например, рассмотрим бесконечное множество натуральных целых чисел, обозначенное как N. Выделим из него такие элементы, которые будут отвечать заданным свойствам – четность, и расположение в интервале от 1 до 11. Это числа 2, 4, 6, 8, 10. Эти пять элементов формируют особую группу, отвечающую общим свойствам, заданным в условии. При этом все члены группы принадлежат множеству натуральных чисел. Такие внутренние объединения именуются подмножествами.
Подмножество – это внутренняя группа элементов множества, все члены которой строго принадлежат данному множеству. Этот набор также принято обозначать большими латинскими группами – например, вышеуказанный пример из пяти элементов можно обозначить, как подмножество S. Стоит сразу отметить, что любое подмножество само по себе является независимым множеством. Приставка под- обозначает только факт принадлежности всех членов данной группы к более широкому набору элементов, относящихся к большому множеству. С другой стороны, такое объединяющее множество именуют надмножеством. Из нашего примера следует, что множество N натуральных чисел включает подмножество S чисел, отвечающих условиям четности, и расположения в интервале (1, 11). Иначе можно сказать, что множество S, состоящее из пяти натуральных чисел, относится к надмножеству N, содержащему все натуральные числа.
Взаимоотношения между различными группами элементов могут быть самыми разнообразными. То же множество натуральных чисел может включать практически бесконечное количество различных группировок – подмножеств. В фундаментальном определении теории множеств чисел существует два основных базиса: само множество, как набор элементов, и свойства, задающие этот набор, или описывающие его. Собственно говоря, эти свойства позволяют не только ограничить набор чисел во множестве, но и включить его в состав какого-либо надмножества либо же выделить из него подмножество.
В нашем видеоуроке мы также рассмотрим взаимосвязь между двумя различными независимыми множествами. Например, рассмотрим следующие множества произвольных чисел:
Все элементы множества D встречаются среди членов множеств и S и F. Можно сказать, что D является подмножеством множества S, и подмножеством множества F.
С другой стороны, все элементы множества S совпадают с элементами множества F. Соответственно, и наоборот. Можно обозначить, что S является подмножеством для F, а F, в свою очередь, является подмножеством для S. Но чаще всего говорят, что множества просто равны между собой.
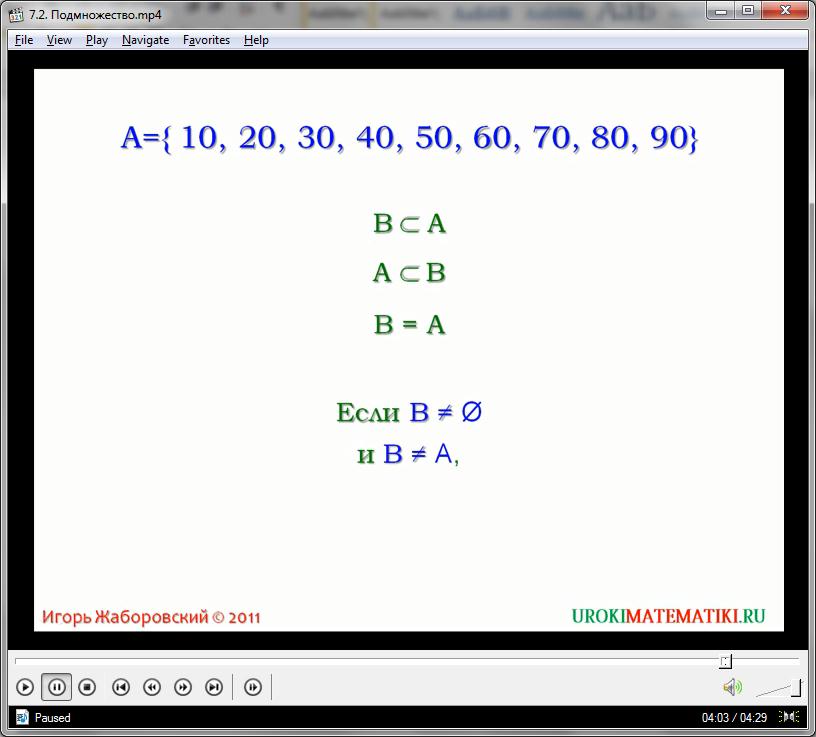
Если любое подмножество А не равно пустому множеству (т.е. содержит хотя бы один элемент), и при этом не равно другому множеству В, то считается, что подмножество А является собственным подмножеством для В. Пустое множество является собственным подмножеством для любого множества, кроме самого себя. С другой стороны, практически все реальные множества являются подмножествами бесконечного множества действительных чисел.
На геометрии подмножества отображаются двумя способами. Собственно геометрический представляет собой линейно-интервальный метод отображения наборов чисел на горизонтальной прямой. Чертится прямая (теоретически бесконечная – как отображение бесконечного надмножества чисел), на ней откладываются заданные числовые отрезки. Например, множество целых чисел от 2 до 10 образуют отрезок АС. Множество четных чисел, состоящих, например, из 2, 4, 6 являются подмножеством для АС, и задаются более коротким отрезком АВ, лежащим на той же прямой, на некотором участке АС.
Но более удобным изображением подмножества являются круги Эйлера. В данном случае, каждое множество представлено правильным кругом. Подмножества выделяются меньшими кругами, вложенными в большой круг. Если подмножество равно самому множеству, то круги совпадают между собой. Если группа элементов не соотносится с каким-либо множеством, то круг группы выходит за пределы этого множества.