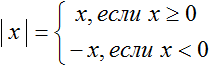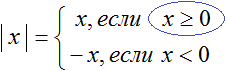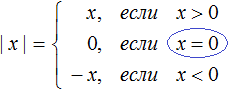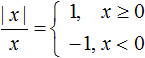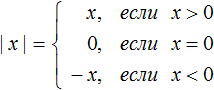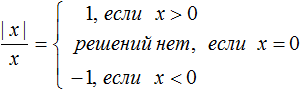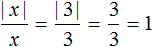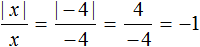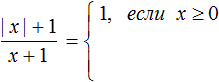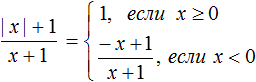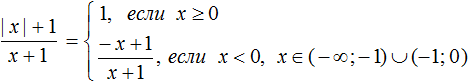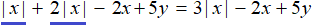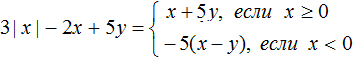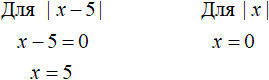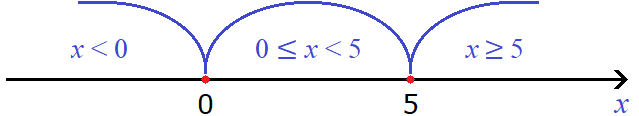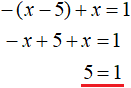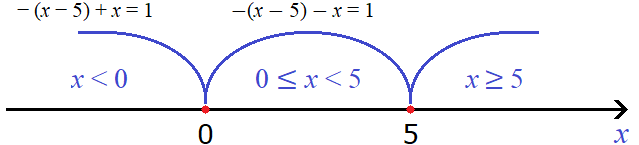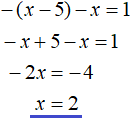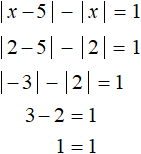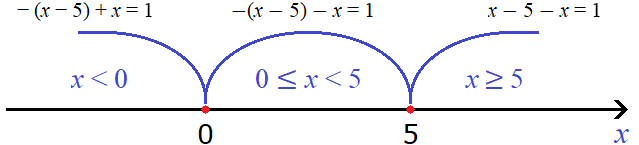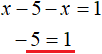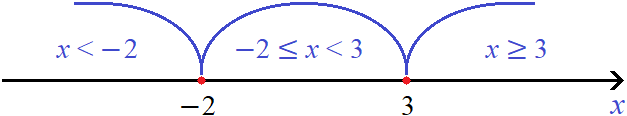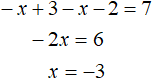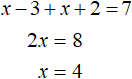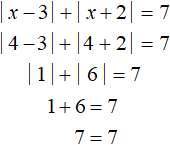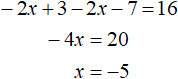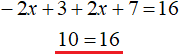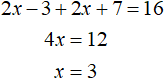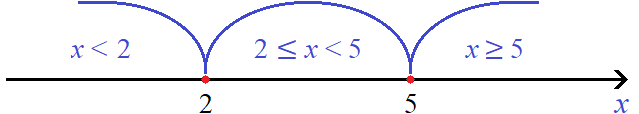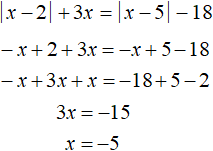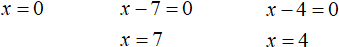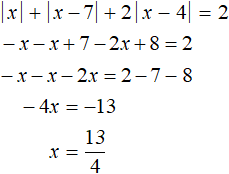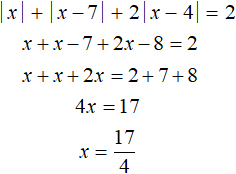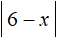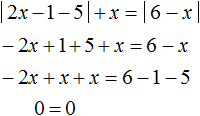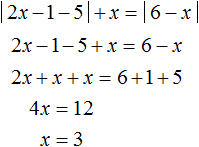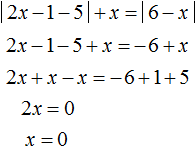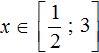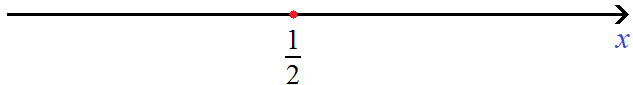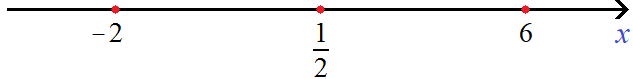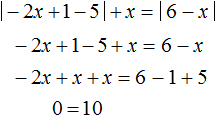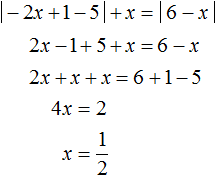Что такое подмодульное выражение

Обобщённое понятие модуля числа

В данном уроке мы рассмотрим понятие модуля числа более подробно.

Что такое модуль?

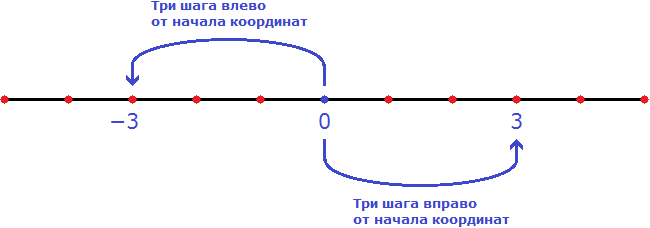
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3

Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:

Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:

Где x₁ и x₂ — числа на координатной прямой.

Например, отметим на координатной прямой числа 2 и 5.

Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:

Видим, что расстояние от числа 2 до числа 5 равно трём шагам:

Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3

То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:

Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:

Это равенство можно прочитать так: Расстояние от x₁ до x₂ равно расстоянию от x₂ до x₁.

Раскрытие модуля

Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.

Правило раскрытия модуля выглядит так:

В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.

Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x

Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5

В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0

Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.

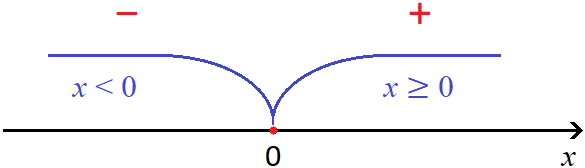
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:

А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:

Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,

Корень из числа 4 равен 2. Тогда модуль примет вид

x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x |√4 − 6| = |2 − 6| = |−4| = −(−4) = 4

На практике обычно рассуждают так:

«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».

Примеры:

|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0

Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:

В данном случае выполняется условие x=0, ведь 0 = 0

Пример 5. Раскрыть модуль в выражении |x|+ 3

Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.

Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:

Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 |x| + 3 = 3 − x = 3 − (−6) = 9

Пример 6. Раскрыть модуль в выражении x +|x + 3|

Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11

Найдём значение выражения x +|x + 3| при x=−3.

Пример 3. Раскрыть модуль в выражении

Как и прежде используем правило раскрытия модуля:

В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0

Перепишем решение так:

Пример 4. Раскрыть модуль в выражении

Но надо учитывать, что при x = − 1 знаменатель выражения 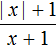обращается в ноль. Поэтому второе условие x следует дополнить записью о том, какие значения может принимать x

Преобразование выражений с модулями

Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.

Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.

Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.

Решение

Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:

В итоге имеем следующее решение:

Пример 2. Раскрыть модуль в выражении: −|x|

Решение

Источник

Алгебра

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Модуль числа

Напомним, что такое модуль числа. Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:

Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:

Именно такое определение обычно и применяется в математике.

Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:

Также модуль возникает при извлечении квадратного корня из четной степени числа:

В частности, если n = 1, получим формулу:

Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:

Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:

В результате получилась «галочка».

Пример. Постройте график ф-ции у = |х 2 – 4х + 3|

Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х 2 – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:

Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х 2 – 4х + 3|, надо перевернуть эту часть графика:

Решение уравнений с модулем

Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число. То есть уравнение имеет вид

где b – какое-то число, а у(х) – произвольная ф-ция.

Если b 10 + 97x 4 – 12,56х 3 + 52х 2 + 1001х – 1234| = – 15

Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.

Ответ: корни отсутствуют.

Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.

Пример. Решите ур-ние

Ясно, что подмодульное выр-ние равно нулю:

Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число. Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:

То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.

Пример. Решите ур-ние

Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.

Пример. Решите ур-ние

Решение. Исходное ур-ние разбивается на два других ур-ния:

10х + 5 = 7 или 10х + 5 = – 7

10х = 2 или 10х = – 12

Пример. Найдите корни ур-ния

Решение. Снова заменим исходное равенство на два других:

x 2 – 2х – 4 = 4 или x 2 – 2х – 4 = – 4

Имеем два квадратных ур-ния. Решим каждое из них:

D = b 2 – 4ас = (– 2) 2 – 4•1•(– 8) = 4 + 32 = 36

Нашли корни (– 2) и 4. Решаем второе ур-ние:

Получили ещё два корня: 0 и 2.

Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:

Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.

Пример. Решите ур-ние

Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:

x 2 + 2x– 1 = х + 1 или x 2 + 2x– 1 = – (х + 1)

х 2 + х – 2 = 0 или х 2 + 3х = 0

D = b 2 – 4ас = 1 2 – 4•1•(– 2) = 1 + 8 = 9

Теперь переходим ко 2-омуур-нию:

Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.

Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.

Пример. Найдите решение уравнения, содержащего модуль:

Решение. Рассмотрим два отдельных равенства:

х 2 + 3,5х – 20 = 4,5х илих 2 + 3,5х – 20 = – 4,5х

х 2 – х – 20 = 0 или х 2 + 8х – 20 = 0

Решим каждое из полученных квадратных ур-ний.

D = b 2 – 4ас = 1 2 – 4•1•(– 20) = 1 + 80 = 81

D = b 2 – 4ас = 8 2 – 4•1•(– 20) = 64 + 80 = 144

Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:

Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.

Мы рассмотрели три случая, когда ур-ние имеет вид:

Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.

Пример. Найдите корни ур-ния

Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:

Если отметить обе точки на прямой, то они образуют на ней 3 интервала:

Исследуем ур-ние на каждом из полученных промежутков.

Так как при х 2 + bx + c = 0

Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.

Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.

Пример. Решите ур-ние

и найдите его корни при значении параметра а, равном 3.

Решение. Вынесем множитель х за скобки:

Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:

Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.

Пример. Решите ур-ние

р 2 х – 3рх = р 2 – 9

Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:

Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.

Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во

Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.

Если р – 3 = 0, то есть р = 3, получится следующее

Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.

Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим

В этом случае ур-ние имеет единственный корень.

Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.

Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.

Пример. Сколько корней имеет ур-ние

при различных значениях параметра b.

Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х 2 – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:

D = b 2 – 4ас = (– 6) 2 – 4•1•5 = 36 + 20 = 16

Итак, нули ф-ции – это точки 1 и 5. Найдем координату х₀ вершины параболы по формуле:

Подставив х₀ в квадратичную ф-цию найдем координату у₀ вершины параболы:

3 2 – 6•3 + 5 = 9 – 18 + 5 = – 4

Теперь построим квадратичную ф-цию:

Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:

Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:

При b 4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.

Ответ: нет корней при b 4; 3 корня при b = 4; 4 корня при 0 4 – (а + 2)х 2 + 3а – 3 = 0

имеет ровно 4 корня?

Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х 2 :

у 2 – (а + 2)у + 3а – 3 = 0 (1)

Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у₁ и у₂. Тогда, проводя обратную замену х 2 = у₁ и х 2 = у₂, мы получим два разных квадратных ур-ния, корни которых будут равны

Если же хоть один из двух корней, например, у₁, окажется равным нулю, то величины

Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у₁ будет отрицательным числом, то ур-ние

вовсе не будет иметь решений, и тогда останется не более 2 корней.

Итак, решим ур-ние (1):

у 2 – (а + 2)у + 3а – 3 = 0

D = b 2 – 4ас = (– (а + 2)) 2 – 4•1•(3а – 3) = (а + 2) 2 – 12 а + 12 =

= а 2 + 4а + 4 – 12а + 12 = а 2 – 8а + 16 = а 2 – 2•4•а + 4 2 = (а – 4) 2

Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4) 2 положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.

Извлечем корень из дискриминанта:

Корни ур-ния (1) можно вычислить по формулам:

И у₁, и у₂ должны быть положительными величинами, однако у₁ меньше, чем у₂ (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:

Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство

Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.

Итак, при условии, что а 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение

можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).

Пример. При каких параметрах а у ур-ния

х 2 – 2(а + 1)х + а 2 + 2а – 3 = 0

существует два корня, которые принадлежат интервалу (– 5; 5)?

Решение. Данное ур-ние является квадратным. Найдем его дискриминант:

D = b 2 – 4ас = (– 2(а + 1)) 2 – 4•1•( а 2 + 2а – 3) = 4(а 2 + 2а + 1) – 4(а 2 + 2а – 3) =

= 4(а 2 + 2а + 1 – а 2 – 2а + 3) = 4•4 = 16

Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам

Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х₁) был больше – 5, больший (это х₂) – меньше – 5:

Значит, должны выполняться два нер-ва

х₁>– 5и х₂ – 5 и а + 3 – 4 и а 1 (-1)

Источник

Решение уравнений с модулем методом интервалов

Уравнения с несколькими модулями в одной части

Чем больше модулей, тем больше приходиться их раскрывать и тем больше получается различных уравнений. Когда модулей один или два — это не сложно. Сложность возникает когда модулей больше двух. Человек может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.

Давайте решим следующее уравнение:

У данного уравнения два модуля в левой части. Оно решается путем раскрытия модулей. Не будем комментировать решение, а сразу приведём его:

Такой вид уравнения удобнее решать методом интервалов (или более точно — методом промежутков). Суть этого метода в том, чтобы разбить координатную прямую на несколько промежутков, а затем решить уравнение на каждом из этих промежутков. Модули исходного уравнения на каждом промежутке будут раскрываться по разному.

Решим уравнение |x − 5| − |x| = 1 методом интервалов.

Для начала нарисуем координатную прямую и обозначим её как x

Если координатная прямая содержит все числа, которые существуют в природе, то логично что она содержит и корни нашего уравнения.

Чтобы найти точки перехода, нужно выяснить при каких значениях x подмодульные выражения равны нулю. Узнать это можно приравняв к нулю подмодульные выражения обоих модулей, и решить обычные линейные уравнения:

Теперь отметим точки перехода на координатной прямой. Мéньшие числа нужно отмечать левее, большие числа правее:

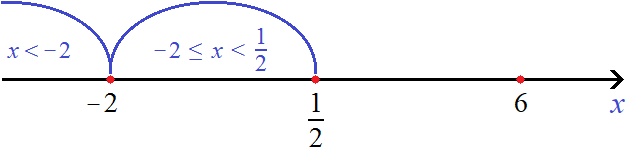
Проведем дуги от точек перехода:

Проще говоря, каждый промежуток включает в себя левый конец, и не включает правый. Сделано это специально, чтобы не допустить потерь значений переменной x. Описать с помощью неравенств нужно все значения на координатной прямой, не допуская их потерь.

Но лучше всего исходить из ситуации, потому что в каких-то случаях левый конец промежутка целесообразнее исключить из рассматриваемого промежутка и включить его в правый конец соседнего промежутка. Об этом мы поговорим позже.

Теперь выясним как будут вести себя модули |x − 5| и |x| на каждом из этих промежутков. От этого будет зависеть то, как они будут раскрываться.

Это уравнение решений не имеет. Значит на промежутке x исходное уравнение не имеет корней. Проще говоря, корень уравнения не является числом меньшим нуля.

Если x больше или равно нулю, но меньше пяти, то подмодульное выражение x − 5, станет отрицательным, а значит модуль |x − 5| на промежутке 0 ≤ x будет раскрываться со знаком минус. Второй модуль |x| на промежутке 0 ≤ x будет раскрываться с плюсом.

В результате после раскрытия модулей на промежутке 0 ≤ x уравнение с модулем |x − 5| − |x| = 1 примет вид −(x − 5) − x = 1

Решим это уравнение:

Если x больше или равно пяти, то модуль |x − 5| на промежутке x ≥ 5 будет раскрываться со знаком плюс. Второй модуль |x| на промежутке x ≥ 5 тоже будет раскрываться с плюсом.

Решим это уравнение:

Это уравнение не имеет решений. Значит на промежутке x ≥ 5 исходное уравнение корней не имеет. Проще говоря, корень уравнения не является числом, бóльшим либо равным пяти.

В итоге корнем уравнения является число 2, которое мы нашли решив исходное уравнение на промежутке 0 ≤ x

Пример 2. Решить уравнение |x − 3| + |x + 2| = 7

Решение

Шаг 1. Находим точки перехода для модулей |x − 3| и |x + 2|

Шаг 2. Отметим на координатной прямой найденные точки перехода и выделим получившиеся промежутки:

Шаг 3. Решим исходное уравнение на каждом промежутке. Для этого посмóтрим как будут раскрываться модули |x − 3| и |x + 2| на этих промежутках.

Следующий модуль |x + 2| на промежутке x тоже будет раскрываться с минусом. Убедимся в этом подставив любые два числа из промежутка x в подмодульное выражение. Например, числа −6 и −8

Значит после раскрытия модулей на промежутке x исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

Обязательно нужно проверить входит ли найденный корень −3 в рассматриваемый промежуток x x найденный корень −3 и проверить верное ли оно. В данном случае неравенство −3 верно, значит корень −3 входит в промежуток x и соответственно является корнем исходного уравнения.

На следующем промежутке −2 ≤ x x ≥ 3 исходное уравнение |x − 3| + |x + 2| = 7 принимает следующий вид:

Решим это уравнение:

Этот корень входит в рассматриваемый промежуток x ≥ 3, значит является корнем исходного уравнения. Проверка также показывает это:

Ответ: −3 и 4.

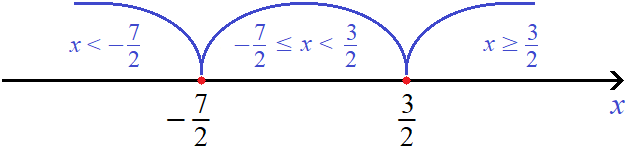
Пример 3. Решить уравнение |2x − 3| + |2x + 7| = 16

Решение

Найдём точки перехода для модулей |2x − 3| и |2x + 7|

Отметим точки перехода на координатной прямой. Меньшие числа нужно отмечать левее, большие правее:

Решим исходное уравнение |2x − 3| + |2x + 7| = 16 на промежутке 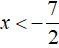. Оба модуля на этом промежутке будут раскрываться с минусом:

Корень −5 принадлежит промежутку 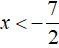, значит является корнем исходного уравнения.

Теперь решим исходное уравнение на промежутке 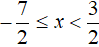. Модуль |2x − 3| на этом промежутке раскрывается с минусом, а модуль |2x + 7| — с плюсом:

Видим, что на промежутке исходное уравнение не имеет решений (корней).

Теперь решим исходное уравнение на промежутке 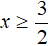. Оба модуля на данном промежутке раскрываются с плюсом:

Корень 3 принадлежит промежутку 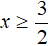, значит является корнем исходного уравнения.

Пример 4. Решить уравнение |x − 2| + 3x = |x − 5| − 18

Решение

Найдём точки перехода для модулей |x − 2| и |x − 5|

Отметим точки перехода на координатной прямой:

Ответ: −5

Пример 5. Решить уравнение |x| + |x − 7| + 2|x − 4| = 2

Решение

Найдём точки перехода для модулей |x|, |x − 7| и |x − 4|

Отметим точки перехода на координатной прямой:

Решим теперь исходное уравнение на промежутке 0 ≤ x |x| на этом промежутке раскрывается с плюсом, а модули |x − 7| и |x − 4| — с минусом:

Решив исходное уравнение на каждом промежутке, мы не нашли корней, удовлетворяющих этому уравнению. Значит данное уравнение не имеет корней.

В ответе можно написать словами, что корней нет (или решений нет), либо указать символ пустого множества. Этот символ будет указывать, что множество корней уравнения |x| + |x − 7| + 2|x − 4| = 2 пусто.

Ответ: ø.

Пример 6. Решить уравнение

Решение

Найдём точки перехода для модулей 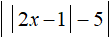и

Если методом интервалов нужно решить уравнение с модулем, который в свою очередь содержит внутри себя другой модуль, то точки перехода надо искать для случаев: когда внутренний модуль раскрывается с плюсом и когда он раскрывается с минусом. Точки перехода будут меняться в зависимости от этих случаев. Давайте посмотрим как это происходит.

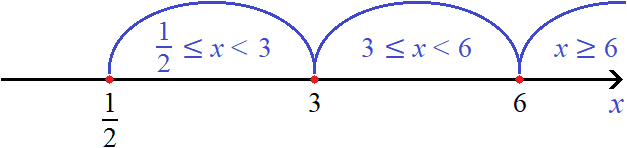
Первый промежуток на котором мы будем решать уравнение это 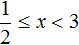. На нем модуль |2x − 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом:

Корень 3 принадлежит рассматриваемому промежутку. Также этот корень удовлетворяет условию 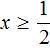, согласно которому внутренний модуль исходного уравнения раскрывается с плюсом.

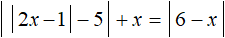
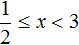
Итак, если внутренний модуль уравнения раскрывается с плюсом, то решениями уравнения являются: промежуток , а также число 3. Запишем эти решения одним промежутком:

Теперь решим исходное уравнение для случая когда внутренний модуль раскрывается с минусом. То есть когда 2x − 1 (что равносильно неравенству 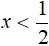). В этом случае исходное уравнение примет вид:

Отметим точку на координатной прямой.

Нас будут интересовать те значения x которые располагаются слева от . Это те значения при которых внутренний модуль исходного уравнения раскрывается с минусом.

Рассматривать будем только те промежутки, которые располагаются слева от . Только при них внутренний модуль исходного уравнения раскрывается с минусом

Это уравнение решений не имеет. Значит на промежутке x исходное уравнение не имеет корней.

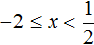
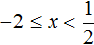
Решим теперь уравнение на промежутке 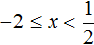. Замечаем, что при подстановке левого конца этого промежутка (числа −2) в модуль |−2x + 1 − 5| данный модуль раскрывается с плюсом, а при остальных значениях промежутка модуль |−2x + 1 − 5| раскрывается с минусом.

На промежутке модуль |−2x + 1 − 5| раскрывается с минусом, а модуль |6 − x| с плюсом. Тогда:

Задания для самостоятельного решения

Примечание: Решения, не удовлетворяющие исходному уравнению, подчёркнуты красным.

Источник