Что такое подобие в жизни
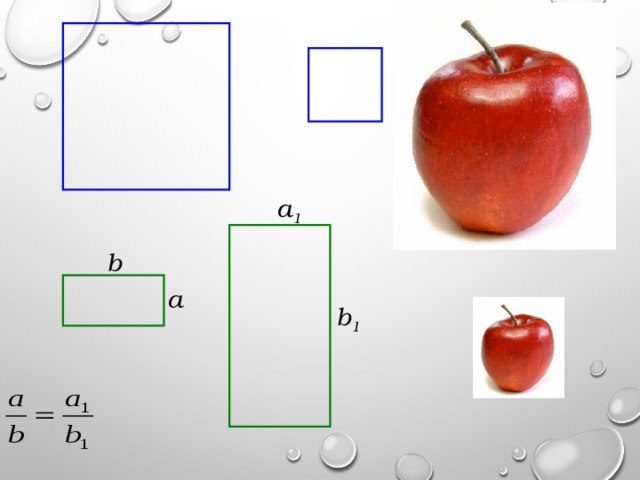
Подобие фигур вокруг нас
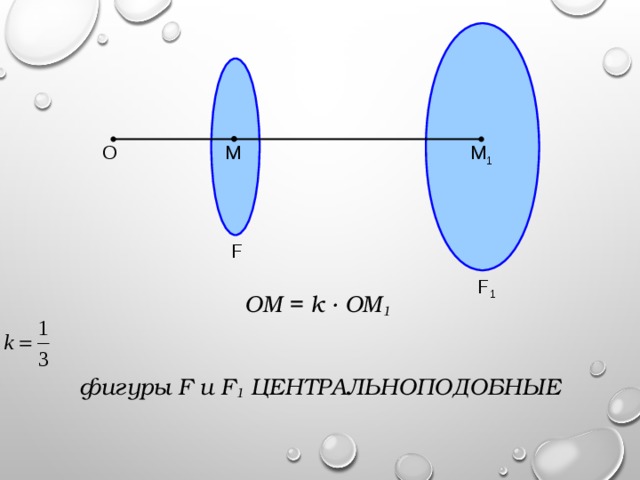
фигуры F и F1 называются ПОДОБНЫМИ, если каждой точке фигуры F можно сопоставить точку фигуры F1 так, что для любых двух точек М и N фигуры F и сопоставленных им точек М1 и N1 фигуры F1 выполняется равенство , где k – одно и то же положительное число для всех точек
Содержимое разработки
ПОДОБИЕ ФИГУР ВОКРУГ НАС
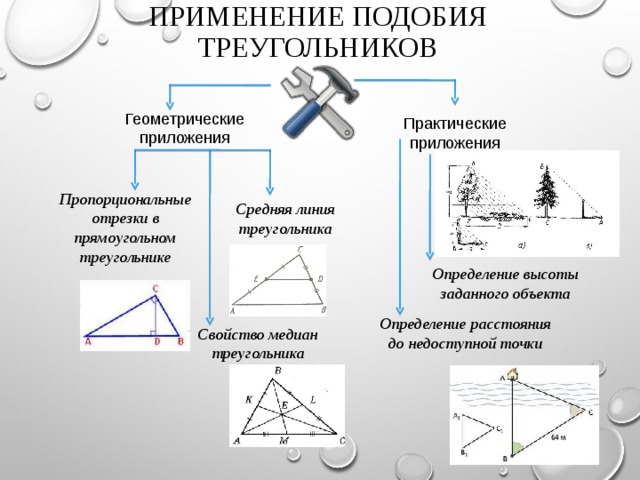
ПРИМЕНЕНИЕ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Пропорциональные отрезки в прямоугольном треугольнике
Средняя линия треугольника
Определение высоты заданного объекта
Определение расстояния до недоступной точки
Свойство медиан треугольника
О подобии произвольных фигур
k – КОЭФФИЦИЕНТ ПОДОБИЯ фигур F и F 1
фигуры F и F 1 ЦЕНТРАЛЬНОПОДОБНЫЕ
ПОДОБИЕ В НАШЕЙ ЖИЗНИ
ВОКРУГ НАС ВЕЛИКОЕ МНОЖЕСТВО ПОДОБНЫХ ФИГУР. ПОДОБИЕ НАС ОКРУЖАЕТ. ВОТ НЕКОТОРЫЕ ПРИМЕРЫ ИЗ НАШЕЙ ЖИЗНИ.
Применение подобия в реальной жизни (презентация)
Скажи мне и я забуду,
Покажи, и я запомню.
Дай мне действовать самому
Китайская мудрость
Урок, обучающий учащихся применять на практике подобия треугольников
Просмотр содержимого документа
«Применение подобия в реальной жизни (презентация)»
Скажи мне и я забуду,
Покажи, и я запомню.
Дай мне действовать самому
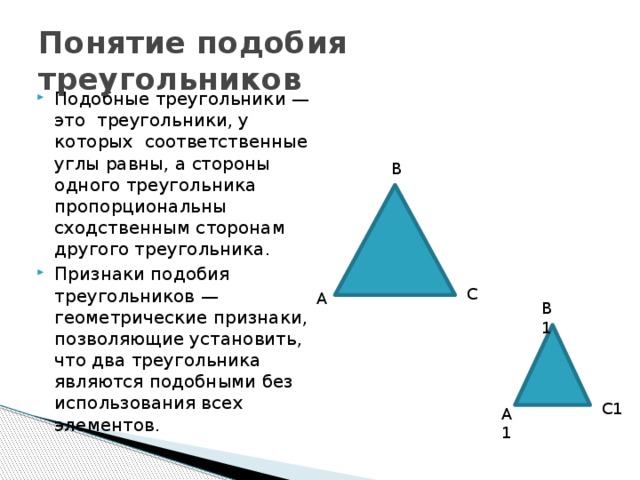
Понятие подобия треугольников
Применение в жизни
Применение подобия треугольников в жизни
Определение высоты пирамиды
Нахождения четвертого неизвес неизвестного члена
Определение высоты предмета
Определение высоты предмета
АВ D подобен EFD (по двум углам) :
В подобных треугольниках сходственные стороны пропорциональны :
1. Шла баба в Москву и повстречала трёх мужиков. Каждый из них нёс по мешку, в каждом мешке по кошке. Сколько существ направлялось в Москву?
3. Две женщины отправились в Троице-Сергиеву Лавру. Обе они прошли 60 вёрст. Сколько вёрст прошла каждая, если шли они с одинаковой скоростью?
4. Какое число делится на все числа без остатка?
5.Электропоезд идёт с востока на запад, ветер дует с севера на юг. В какую сторону отклоняется дым?
6. На дереве сидело 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве? *
Используя карточку определите ширину реки с помощью травинки.
Проектная работа на тему «Применение подобия треугольников в жизни»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
CLK=> 15/3=5=> MD=3*5=15м. Ответ. » data-title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD
CLK=> 15/3=5=> MD=3*5=15м. Ответ. » >
Описание презентации по отдельным слайдам:
Проектная работа на тему: Подобие треугольников и применение их в жизни. Выполнили: ученики 8 класса Чикоткова Арина Ногих Анна Руководитель: учитель математики Фурсенко Н.П. Лизиновка 2016 МКОУ Лизиновская СОШ
Задачи и цели: Узнать где применяется подобие в жизни. Рассмотреть решение задач на местности.
Немного из истории Определение высоты пирамиды по длине ее тени
За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени.
На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.
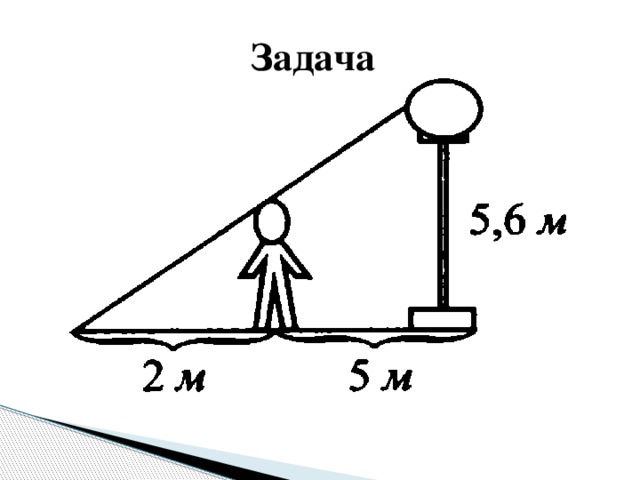
Применение теории на практике: Определение высоты предмета По шесту. Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева будет равна линии, проведенной от вашей головы до основания дерева.
CLK=> 15/3=5=> MD=3*5=15м. Ответ. » title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD
CLK=> 15/3=5=> MD=3*5=15м. Ответ. «> 
CLK=> 15/3=5=> MD=3*5=15м. Ответ:» title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD
Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD
CLK=> 15/3=5=> MD=3*5=15м. Ответ: дерево высотой 15 м.
10:1.60=6.25 6.25*1.60=10м Ответ : дерево высотой 10 метров 10м
По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас
По зеркалу. АВD подобен EFD (по двум углам): ВАD= FED=90°; АDВ = EDF, т.к. угол падения равен углу отражения. В подобных треугольниках сходственные стороны пропорциональны:
12:1=12 12*1.60=19.2м Ответ: дерево высотой 19.2м 19.2м
Измерение расстояния до недоступной точки. 19.2м 19.2м Палец-0.06м, Расстояние от глаза до пальца-0.5м Расстояние до дерева 160м 19.2:0.06=320 320*0.5=160м
Измерение ширены реки с помощью булавочного прибора
Булавочный прибор для измерений
Также для измерения могут применяться разные инструменты. Экер Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны.
Астролябия Устройство: астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас.
Вывод: Подобие треугольников применяется в повседневной жизни довольно часто. Мы выяснили на конкретных примерах, что с помощью подобия можно найти высоту или расстояние до известной или неизвестной нам точки.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-296066
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Ученые изучили проблемы родителей, чьи дети учатся в госпитальных школах
Время чтения: 5 минут
В Думу внесли законопроект об обязательном образовании для находящихся в СИЗО подростков
Время чтения: 2 минуты
Названы главные риски для детей на зимних каникулах
Время чтения: 3 минуты
АСИ организует конкурс лучших управленческих практик в сфере детского образования
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Как подобие используется на практике
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Как подобие используется на практике.
Геометрия – это не просто наука о свойствах геометрических фигур. Геометрия – это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы. Вступление
Гипотеза Возможно ли применение подобия в практических целях?
Цели и задачи проекта. Узнать: Где можно встретить подобие. Как подобие используют на практике.
ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы у геометрических фигур, независимо от их размеров. Две фигуры F1 и F2 называются подобными, если между их точками можно установить взаимно однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек фигур F1 и F2 равно одной и той же постоянной k, называемой коэффициентом подобия. Углы между соответствующими линиями подобных фигур равны. Тема1: Что такое подобные фигуры?
Тема2: Зачем применяют подобие. Подобие применяют для того чтобы создавать макеты удобные по размеру.
Тема3: примеры подобных фигур в повседневной жизни. Автомобиль т его модель подобные тела.
Карты одной и той же территории, сделанные в разных масштабах, подобны.
картина и её фотография — это подобные фигуры.
Египетские пирамиды подобны друг другу, также любой макет подобен оригиналу, если сделан соблюдая масштаб ко всем размерам.
Правило золотого сечения. Принцип золотого сечения – высшее проявление структурного и функцио- нального совершенства целого и его частей в искусстве, науке, технике и природе. Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. a:b=b:с или c: b=b:a Тема 4. Правило золотого сечения.
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Тема 5 Правило Золотого сечения в живописи.
В этой картине фигура Пушкина также поставлена художником слева на линии золотого сечения. Голова военного, с восторгом слушающего чтение поэта, находится на другой вертикальной линии золотого сечения.
Рассмотрим побег цикория. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечени.я. Тема6: Золотое сечения в природе
У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.
И. Шевелев, изучая архитектуру церкви Покрова на Нерли, выяснил, что в ней проявляется пропорция, представляющая собой отношение большей стороны к диагонали прямоугольника с отношением сторон 1:2. Тема7: Золотое сечения в архитектуре.
Тема8: Что такое подобные треугольники? Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Зная признаки подобия треугольников, можно определить высоту какого-либо предмета или рассчитать расстояние до недоступной точки.
Тема10: Измерение расстояния до недоступно точки. Для нахождения расстояния между двумя точками на местности выберем на плоскости еще одну. Затем измерим расстояние от нее до доступной. Соединим все точки на местности и измерим углы, которые прилегают к известной стороне. Построив на бумаге подобный треугольник и определив отношение сторон двух фигур, с легкостью вычисляем расстояние между точками.
Вывод Таким образом, признаки подобия фигур – одно из важнейших понятий геометрии. Оно широко используется не только в научных целях, но и для других нужд.
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-426584
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Названы главные риски для детей на зимних каникулах
Время чтения: 3 минуты
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
В Думу внесли законопроект об обязательном образовании для находящихся в СИЗО подростков
Время чтения: 2 минуты
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учительница из Киргизии победила в конкурсе Минпросвещения РФ «Учитель-международник»
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
«Подобие фигур в жизни»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Выбранный для просмотра документ pril1.ppt
Описание презентации по отдельным слайдам:
Уже в XVI в. нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.
Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей. Вот один пример из «Устава ратных, пушечных и других дел, касающихся до военной науки»:
За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени. ПРИТЧА:
На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.
Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида. СЕ=ED, т.е. H=b Преимущества: не требуются вычисления. Недостатки: нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.
«Таинственный остров» (фр. L’Île mystérieuse) — роман-робинзонада французского писателя впервые опубликованный в 1874 году. Является продолжением известных произведений Верна «20000 лье под водой» и «Дети капитана Гранта». В книге повествуется о событиях, происходящих на вымышленном острове, где остановился капитан Немо на своей подводной лодке «Наутилус». Основными персонажами являются пятеро американцев, которые оказываются на необитаемом острове в Южном полушарии.
Нахождения четвертого неизвестного члена пропорции. Преимущества: можно производить измерения в любую погоду; простота формулы. Недостатки: нельзя измерить высоту предмета не испачкавшись, так как приходится ложиться на землю.
Преимущества: можно производить измерения в любую погоду; одежда будет чистой; простота формулы; Недостатки: нужно специальное приспособление: зеркало.
По построению АВС подобен А1В1С1 (по двум углам). В подобных треугольниках сходственные стороны пропорциональны: А В С А1 В1 С1
Нахождение ширины озера Длина тени земного шара
Выбранный для просмотра документ Природа говорит языком математики.doc
Природа говорит языком математики.
Геометрия всегда решала те задачи, которые перед ней ставила жизнь. Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие детские игрушки подобны предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, две фотографии разного формата.
Мы уже знаем, что в геометрии фигуры одинаковой формы принято называть подобными. Сегодня мы обсудим, как свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности.
При помощи подобных треугольников можно измерить огромные расстояния и высоты используя подручные средства, т.е. мы будем решать две задачи:
определение высоты предмета;
определение расстояния до недоступного объекта.
Уже в XVI в. В России нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.
Вот один пример. Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей.
Рассмотрим несколько случаев из истории и литературы.
1. Определение высоты предмета по длине его тени.
Греческие ученые решили множество практических задач, которые до них люди не умели решать. Например, за шесть веков до нашей эры греческий мудрец Фалес Милетский научил египтян определять высоту пирамиды по длине ее тени.
Как это было, рассказывается в книге Я.И. Перельмана «Занимательная геометрия».Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени.
Я хочу прочитать вам эту маленькую притчу.
«Усталый северный чужеземец пришел в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона и что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.
— Зовут меня Фалес. Родом я из Милета.
Жрец надменно продолжал:
— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.
На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Он измерил тень от палки и тень от пирамиды. Сравнивая соотношения высот реальных предметов с длинами их теней, Фалес нашел высоту пирамиды.
Определение высоты пирамиды по длине ее тени.





В подобных треугольниках сходственные стороны пропорциональны:


Таким образом, Фалес нашел высоту пирамиды.
Преимущества способа Фалеса:
не требуются вычисления.
нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.
2. Определение высоты предмета по шесту.
При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, которыйживописнопредставлен у Жюль Верна в известном романе «Таинственный остров».
Читаем отрывок из романа.
— Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.
Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.
Взяв прямой шест, длиной 10 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки.
Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком.
— Помнишь свойства подобных треугольников?
— Их сходственные стороны пропорциональны.
— Да, и, следовательно, если мы измерим два расстояния, то зная высоту шеста, сможем вычислить четвёртый неизвестный член пропорции, т.е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты.
Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.
По окончании измерений инженер составил следующую запись:
Н 
Значит, высота гранитной стены равнялась приблизительно 333 футам».
Преимущества способа Жюль Верна:
— можно производить измерения в любую погоду;
нельзя измерить, высоту предмета не испачкавшись, так как приходится ложиться на землю.
3. Определение высоты предмета.
Есть несколько простых способов определения высоты предметов. Например, такие способы приведены в настольной книге охотника-спортсмена.
По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.
Вместо лужицы можно пользоваться положенным горизонтально зеркальцем. Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека.





В подобных треугольниках сходственные стороны пропорциональны:


Таким образом, найдена высота объекта.
4. Определение расстояния до недоступного объекта.
Рассмотрим применение подобия треугольников к определению расстояния до недоступного объекта. Слайд 19-25 (Презентация 1, с использованием Приложения 1 ).
6. Рассмотрение и обсуждение примеров. Слайды 27-28 (Презентация 1).
7. Дополнительный материал. Слайд 29-30