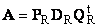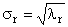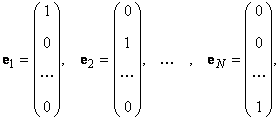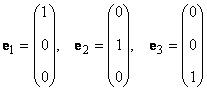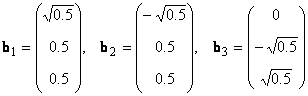Что такое подобные матрицы
Подобные матрицы
Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что:
Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных координатных системах; при этом матрица Р является матрицей перехода от одной системы к другой.
Если две матрицы подобны, то говорят, что одна из матриц может быть получена преобразованием подобия из другой. Если при этом одна из матриц диагональная, то про вторую матрицу говорят, что она может быть диагонализована.
Свойства
Отношение подобности матриц является отношением эквивалентности в пространстве квадратных матриц.
У подобных матриц совпадают многие характеристики, а именно:
Канонические формы подобных матриц
Часто возникает вопрос, насколько сильно можно упростить вид заданного линейного преобразования путем замены базиса (т.е. системы координат). Поскольку получающиеся при этом матрицы подобны, то это то же самое, что и поиск некоторой канонической формы матрицы в классе эквивалентности матриц, подобных матрице этого линейного преобразования.
Простейшей такой формой была бы, конечно, диагональная матрица, но не все матрицы могут быть приведены к диагональному виду (важное исключение составляют симметричные действительные и эрмитовы матрицы, которые всегда могут быть диагонализованы).
Существует несколько более сложных канонических форм матриц, к которым может быть приведена любая матрица преобразованием подобия:
Литература
Полезное
Смотреть что такое «Подобные матрицы» в других словарях:
подобные матрицы — математические матрицы, имеющие аналогичную структуру, каждый из элементов которых может иметь различное значение. На многих языках программирования математические преобразования над подобными матрицами описываются довольно компактно и просто.… … Энциклопедический словарь по психологии и педагогике
подобные матрицы — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
Подобные матрицы — квадратные матрицы (См. Матрица) А и В порядка n, связанные соотношением В = Р 1АР, где Р какая либо неособенная (т. е. имеющая обратную) матрица того же порядка. При задании матрицей линейного преобразования (См. Линейное преобразование) … Большая советская энциклопедия
ПОДОБНЫЕ МАТРИЦЫ — квадратные матрицы Аи Водного порядка, связанные соотношением В=S 1AS, где S какая либо невырожденная матрица того же порядка. П. м. имеют один и тот же ранг, один п тот же определитель, один и тот же характеристич. многочлен, одни и те же… … Математическая энциклопедия
matrices semblables — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
panašiosios matricos — statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
similar matrices — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
ähnliche Matrizen — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
Финансовая пирамида — (Financial Pyramid) Финансовая пирамида это денежная структура, которая аккумулирует денежные средства путем постоянного привлечения новых инвесторов Финансовая пирамида: список финансовых пирамид, борьба с финансовыми пирамидами, финансовые… … Энциклопедия инвестора
Фондирование — (Funding) Фондирование это процесс финансирования активных операций банка Ставка и коэффициент фондирования при расчетах матрицы, целевое фондирование и его источники Содержание >>>>>>>>> … Энциклопедия инвестора
ПОДОБНЫЕ МАТРИЦЫ
Смотреть что такое «ПОДОБНЫЕ МАТРИЦЫ» в других словарях:
Подобные матрицы — Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что: Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных… … Википедия
подобные матрицы — математические матрицы, имеющие аналогичную структуру, каждый из элементов которых может иметь различное значение. На многих языках программирования математические преобразования над подобными матрицами описываются довольно компактно и просто.… … Энциклопедический словарь по психологии и педагогике
подобные матрицы — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
Подобные матрицы — квадратные матрицы (См. Матрица) А и В порядка n, связанные соотношением В = Р 1АР, где Р какая либо неособенная (т. е. имеющая обратную) матрица того же порядка. При задании матрицей линейного преобразования (См. Линейное преобразование) … Большая советская энциклопедия
matrices semblables — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
panašiosios matricos — statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
similar matrices — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
ähnliche Matrizen — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
Финансовая пирамида — (Financial Pyramid) Финансовая пирамида это денежная структура, которая аккумулирует денежные средства путем постоянного привлечения новых инвесторов Финансовая пирамида: список финансовых пирамид, борьба с финансовыми пирамидами, финансовые… … Энциклопедия инвестора
Фондирование — (Funding) Фондирование это процесс финансирования активных операций банка Ставка и коэффициент фондирования при расчетах матрицы, целевое фондирование и его источники Содержание >>>>>>>>> … Энциклопедия инвестора
Подобные матрицы
Смотреть что такое «Подобные матрицы» в других словарях:
Подобные матрицы — Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что: Подобные матрицы получаются при задании одного и того же линейного преобразования матрицей в разных… … Википедия
подобные матрицы — математические матрицы, имеющие аналогичную структуру, каждый из элементов которых может иметь различное значение. На многих языках программирования математические преобразования над подобными матрицами описываются довольно компактно и просто.… … Энциклопедический словарь по психологии и педагогике
подобные матрицы — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
ПОДОБНЫЕ МАТРИЦЫ — квадратные матрицы Аи Водного порядка, связанные соотношением В=S 1AS, где S какая либо невырожденная матрица того же порядка. П. м. имеют один и тот же ранг, один п тот же определитель, один и тот же характеристич. многочлен, одни и те же… … Математическая энциклопедия
matrices semblables — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
panašiosios matricos — statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
similar matrices — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
ähnliche Matrizen — panašiosios matricos statusas T sritis fizika atitikmenys: angl. similar matrices vok. ähnliche Matrizen, f rus. подобные матрицы, f pranc. matrices semblables, f … Fizikos terminų žodynas
Финансовая пирамида — (Financial Pyramid) Финансовая пирамида это денежная структура, которая аккумулирует денежные средства путем постоянного привлечения новых инвесторов Финансовая пирамида: список финансовых пирамид, борьба с финансовыми пирамидами, финансовые… … Энциклопедия инвестора
Фондирование — (Funding) Фондирование это процесс финансирования активных операций банка Ставка и коэффициент фондирования при расчетах матрицы, целевое фондирование и его источники Содержание >>>>>>>>> … Энциклопедия инвестора
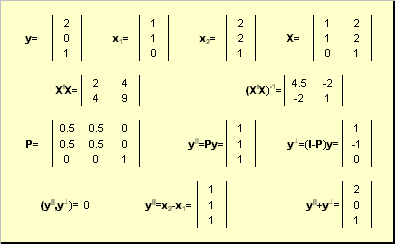
Эквивалентные и подобные матрицы
Две прямоугольные матрицы A и B одной размерности I×J эквивалентны, если существуют такие квадратные матрицы S, размерности I×I, и T, размерности J×J, что
Эквивалентные матрицы имею один и тот же ранг.
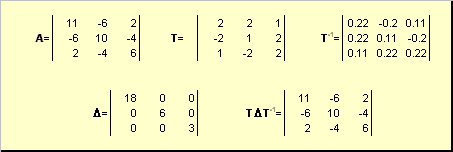
Две прямоугольные матрицы A и B одной размерности N×N подобны, если существует такая невырожденная матрица T, что
Матрица T называется преобразованием подобия.
Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.
Приведение матрицы к диагональному виду
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —
Здесь Λ = diag(λ1. λN) — это диагональная матрица, элементами которой являются собственные значения матрицы A, а T — это матрица, составленная из соответствующих собственных векторов матрицы A, т.е. T = (v1. vN).
Рис. 23 Приведение к диагональному виду
Разложение по сингулярным значениям (SVD)
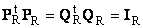
QR — матрица, образованная R ортонормированными собственными векторами qr матрицы A t A;
Рис. 24 SVD разложение
Дополняя матрицы PR и QR ортонормированными столбцами, а матрицу DR нулевыми значениями, можно сконструировать матрицы P (I×J), D (J×J) и Q (J×J) такие, что
Об использовании SVD рассказано в пособиях MatLab. Руководство для начинающих и Метод главных компонент (PCA)
Линейное пространство
Базис линейного пространства
в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = (x1, x2. xN) t может быть представлен как линейная комбинация x = x1e1+ x2e2+. +xNeN базисных векторов.
Базис, составленный из попарно ортогональных векторов, называется ортогональным, а если базисные вектора еще и нормированы, то этот базис называется ортонормированным.
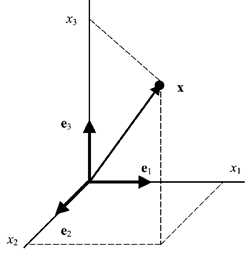
Геометрическая интерпретация
Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N-мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x = (x1, x2. xN) t можно изобразить точкой в этом пространстве с координатами (x1, x2. xN).
Рис. 25 Координатное пространство
Множественность базисов
В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса
можно установить и другой ортонормированный базис, например
Каждый базис можно представить матрицей B = (b1. bN), составленной из базисных векторов. Переход от одного базиса к другому осуществляется с помощью невырожденной квадратной матрицы T, т.е. B2 = TB1.
Подпространство
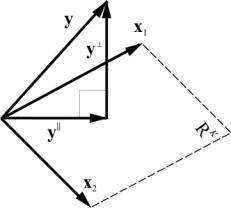
Проекция на подпространство
Рис. 26 Проекция на подпространство
Проекциюy || можно представить как результат действия проекционной матрицы P
Проекционная матрица определяется как
Рис. 27 Проекционное разложение
Заключение
Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.
Что такое подобные матрицы
Положение предприятия нанесено на подобной матрице на рис. 12. [c.232]
Подобная матрица позволяет сбалансировать доходную и расходную части и [c.164]
С подобной матрицей мы уже имели дело на четвертом этапе [c.124]
Процедура анализа систем состоит в выделении всех возможных следствий из альтернативных систем для выбора из них наилучшей. За такую систему принимается та, которая в большей степени отвечает поставленным целям. При анализе некоторые сведения получаются объективно, т. е. путем сбора опытных данных и нахождения распределения частот, другие — субъективно, путем интуитивного восприятия относительных частот, неявно отражающего объективные частоты. Для выбора оптимальной системы в условиях определенности, когда все следствия определены по шкале отношений, можно воспользоваться аппаратом математического программирования. Дело осложняется, когда следствия недостоверны, взаимозависимы и требуют различных шкал измерений. Какой-либо методики оптимизации рекомендовать здесь невозможно. Приводя в качестве метода оптимизации таблицу, подобную матрице решений, А. Холл обращает внимание на необходимость учета не только математического ожидания оценки следствия, но и дисперсии, показывая, что недостаточное внимание к последней может привести к существенным просчетам. [c.16]
Таким образом, характеристический многочлен зависит только от линейного оператора и не зависит от выбора базиса. Сформулируем этот результат иначе характеристические многочлены подобных матриц совпадают. [c.498]
Подобные матрицы, 497 Полная коллинеарность, 109, [c.573]
Очевидно, прямолинейное представление подобной матрицы невозможно, поскольку она очень велика и разрежена (т.е. большинство клеток в ней пусты). В операционных системах более [c.235]
На основе подобных матриц комплектуется состав подразделений и выявляются взаимосвязи между ними. [c.46]
Подобную матрицу целесообразно использовать при разработке стратегических планов наращивания ресурсных возможностей нефтяной компании. [c.437]
Методом дерева решений можно пользоваться в ситуациях, подобных описанной выше, в связи с рассмотрением платежной матрицы. В этом случае предполагается, что данные о результатах, вероятности и т.п. не влияют на все последующие решения. Однако дерево решений можно построить под более сложную ситуацию, когда результаты одного решения влияют на последующие решения. Таким образом, дерево решений — это полезный инструмент для принятия последовательных решений. [c.238]
Если по всем блокам, составляющим данный объект, выполняется указанное соотношение, то этот объект с определенным временным лагом на доставку в Северные районы и поставками ресурсов от других поставщиков необходимо считать готовым к монтажу. Поэтому в матрице, описывающей строительство, подобные объекты и составляющие их блоки, материалы, оборудование должны выступать в роли «потребителей монтажных работ». [c.105]
Для токарного участка эта величина равна 2500 ДМ и является результатом распределения затрат или, точнее, получена из целевой матрицы покрытия, построенной для предоставляющих и получающих услуги МВЗ в соответствии с некоторыми коэффициентами. Поскольку такое распределение осуществляется внутри блока постоянных затрат, оно не влияет на систему расчетов по суммам покрытия. В принципе, можно было бы сразу перенести постоянные затраты неосновных, или вторичных, МВЗ в расчеты результатов по продуктам. Однако на основе подобных производственных затрат [c.218]
Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения [c.241]
Несмотря на всю привлекательность подобных подходов, основанных на рассмотренных матрицах, они обладают и рядом недостатков. Они достаточно трудоемки и дорогостоящи, ряд показателей с их помощью трудно измерить, да- [c.42]
На матрице видно, что данная компания владеет только одной «звездой», и небольшой размер окружности указывает на то, что доходы, полученные от сбыта этого товара, невелики. Незначительную прибыль приносят и две «дойные коровы». При этом компания владеет сразу четырьмя «собаками» и четырьмя «трудными детьми». Такой портфель считается несбалансированным, поскольку «трудных детей» и «собак» слишком много, а «звезд» и «дойных коров» недостаточно. В подобной ситуации большинство компаний равномерно распределяет полученный незначительный излишек наличности между ассортиментами товаров на растущих рынках [40]. В этом случае на [c.232]
Метод сканирования. Чтобы сберечь время и деньги при поиске рынка, иногда применяют так называемый метод сканирования. Суть его в том, что исследователь задает или ранжирует приоритеты, которым должен отвечать будущий рынок сбыта. Формируется матрица, где сгруппированы задаваемые параметры. Если параметр не отвечает заданным условиям, данный рынок и все ему подобные, составляющие своеобразный пласт, снимаются с рассмотрения либо изучаются во вторую очередь. [c.55]
В литературе подобные системы часто называют системами одновременных уравнений, имея в виду, что здесь зависимая переменная одного уравнения может появляться одновременно в виде переменной (но уже в качестве независимой) в одном или нескольких других уравнениях. В таком случае теряет смысл традиционное различение зависимых и независимых переменных. Вместо этого устанавливается различие между двумя видами переменных. Это, во-первых, совместно зависимые переменные (эндогенные), влияние которых друг на друга должно быть исследовано (матрица А в слагаемом Ay t) приведенной выше системы уравнений). Во-вторых, предопределенные переменные, которые, как предполагается, оказывают влияние на первые, однако не испытывают их воздействия это переменные с запаздыванием, т.е. лаговые (второе слагаемое) и определенные вне данной системы уравнений экзогенные переменные. [c.400]
Сравнение стран по экономическим показателям наиболее удобно при разработке транснациональной или многонациональной маркетинговых стратегий, когда операции в одной стране почти не отражаются на деятельности компании в других странах. В подобной ситуации она может эффективно распределять свои ресурсы, переходя от стран с наивысшим ожидаемым результатом к странам, где нужно учитывать риск и неопределенность. При разработке глобальной стратегии необходимо проводить сравнение стран по признаку конкурентных возможностей компаний (наиболее известна матрица сравнения стран компании «Форд» ), а также по уровню риска (рассматриваются все возможные риски политические, валютные и др.). [c.190]
Здесь и далее каждое из подобных неравенств с min и max в матрице подзадачи, вводимой в ЭВМ, записываются в виде двух неравенств L