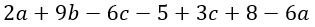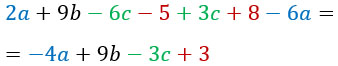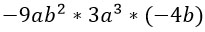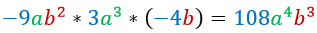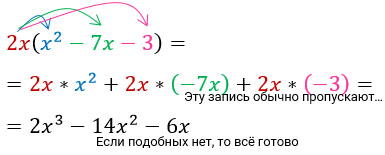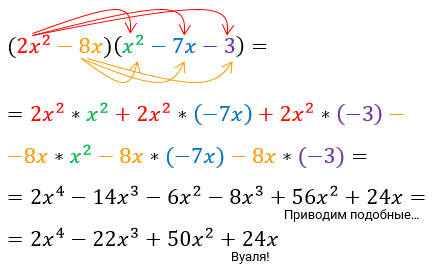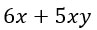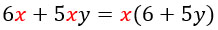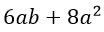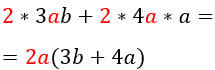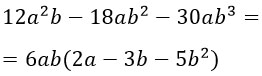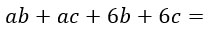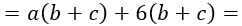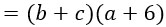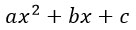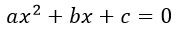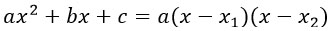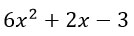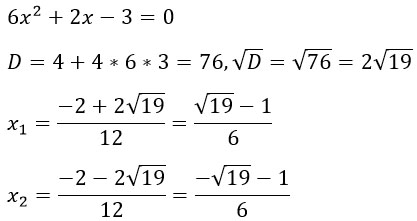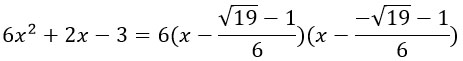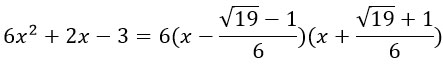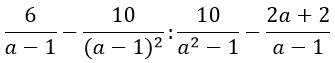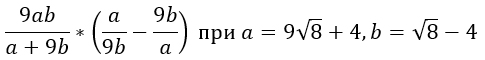Что такое подобные в алгебре 7 класс

Подобные слагаемые, их приведение, примеры.

Одним из наиболее часто используемых тождественных преобразований является приведение подобных слагаемых. В этой статье мы дадим определение подобных слагаемых, разберемся, что называют приведением подобных слагаемых, рассмотрим правила, по которым выполняется это действие, и приведем примеры приведения подобных слагаемых с подробным описанием решения.

Навигация по странице.

Определение и примеры подобных слагаемых.

Разговор о подобных слагаемых возникает после знакомства с буквенными выражениями, когда возникает необходимость проведения преобразований с ними. По учебникам математики Н. Я. Виленкина определение подобных слагаемых дается в 6 классе, и оно имеет следующую формулировку:

Подобные слагаемые – это слагаемые, которые имеют одинаковую буквенную часть.

Стоит внимательно разобраться в этом определении. Во-первых, речь идет о слагаемых, а, как известно, слагаемые являются составными элементами сумм. Значит, подобные слагаемые могут присутствовать лишь в выражениях, которые представляют собой суммы. Во-вторых, в озвученном определении подобных слагаемых присутствует незнакомое понятие «буквенная часть». Что же понимают под буквенной частью? Когда дается это определение в шестом классе, под буквенной частью понимается одна буква (переменная) или произведение нескольких букв. В-третьих, остается вопрос: «А что же это за такие слагаемые с буквенной частью»? Это слагаемые, представляющие собой произведение некоторого числа, так называемого числового коэффициента, и буквенной части.

Дальше из контекста указанного выше учебника становится видно дополнение к определению подобных слагаемых – слагаемые в буквенном выражении, не имеющие буквенной части, также называют подобными.

Позже расширяется и понятие буквенной части – буквенной частью начинаю считать не только произведение букв, а произвольное буквенное выражение. К примеру, в учебнике алгебры для 8 класса авторов Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова под редакцией С. А. Теляковского приведена сумма вида , и сказано, что составляющие ее слагаемые являются подобными. Общей буквенной частью этих подобных слагаемых является выражение с корнем вида .

Обобщив всю изложенную информацию, можно дать следующее определение подобных слагаемых.

Подобными слагаемыми называются слагаемые в буквенном выражении, имеющие одинаковую буквенную часть, а также слагаемые, не имеющие буквенной части, где под буквенной частью понимается любое буквенное выражение.

Отдельно скажем, что подобные слагаемые могут быть одинаковыми (когда равны их числовые коэффициенты), а могут быть и разными (когда их числовые коэффициенты различны).

Приведение подобных слагаемых, правило, примеры

Приведение подобных слагаемых проводится в три этапа:

Для удобства три перечисленных выше шага объединяют в правило приведения подобных слагаемых: чтобы привести подобные слагаемые, нужно сложить их коэффициенты и полученный результат умножить на буквенную часть (если она есть).

Для закрепления материала рассмотрим решение еще одного примера.

Источник

Подобные слагаемые. Приведение подобных слагаемых

Подобные слагаемые – это одночлены, у которых одинаковы буквенные множители.

одночлены \(2\)\(x\) и \(5\)\(x\) – подобны, так как и там, и там буквы одинаковы: икс;

одночлены \(x^2y\) и \(-2x^2y\) – подобны, так как и там, и там буквы одинаковы: икс в квадрате, умноженный на игрек. То, что перед вторым одночленом стоит знак минус не играет роли, просто у него отрицателен числовой множитель ( коэффициент );

одночлены \(3xy\) и \(5x\)– не подобны, так как в первом одночлене буквенные множители икс и игрек, а во втором – только икс;

Приведение подобных слагаемых

Подобные слагаемые можно складывать и вычитать, заменяя сложные выражения на более простые. Например, выражение \(2x+5x\) без проблем можно заменить на \(7x\). Логика такой замены понятна из пояснения выше:

Процесс замены суммы или разности подобных слагаемых одним одночленом называется «приведение подобных слагаемых».

Отметим при этом, что если слагаемые не подобны, то привести их не получится. Например, в сложить \(2x^2\) и \(3x\) – нельзя, они же разные!

Пример. Решить уравнение \(7x^2+3x-7x^2-x=6\)

В левой части уравнения есть подобные слагаемые: \(7x^2\) и \((-7x^2)\), а также \(3x\) и \((-x)\). Перепишем уравнение так, чтоб они стояли рядом. Для этого меняем местами слагаемые одночлены, не забывая сохранять знаки.

Каждый раз переписывать уравнение так, чтоб подобные стояли рядом совсем необязательно, можно приводить их сразу. Здесь это было сделано для наглядности дальнейших преобразований.

Хочу задать вопрос

Присоединяйтесь к нашей группе ВКонтакте

Смотрите нас в YouTube

Источник

Подобные слагаемые, их приведение, примеры

Приведение подобных слагаемых является одним из наиболее употребимых тождественных преобразований. В этом разделе мы дадим определение термина, разберем, что обозначает словосочетание «приведение подобных слагаемых», рассмотрим основные правила выполнения действий и наиболее распространенные типы задач.

Определение и примеры подобных слагаемых

В большинстве учебных пособий тема подобных слагаемых разбирается после знакомства с буквенными выражениями, когда появляется необходимость проводить с ними различные преобразования.

Подобные слагаемые – это слагаемые, которые имеют одинаковую буквенную часть.

Слагаемые – это, как известно, составные элементы суммы. Это значит, что они могут присутствовать лишь в тех выражениях, которые представляют собой сумму. Буквенная часть – это одна или произведение нескольких букв, которые представляют собой переменные. Слагаемые с буквенной частью – это произведение некоторого числа и буквенной части. Здесь некоторое число также носит название числового коэффициента.

Буквенная часть может быть представлена не только произведением букв, но также и произвольным буквенным выражением. Например:

Обобщим изложенные выше утверждения и дадим еще одно определение подобных слагаемых.

Подобные слагаемые – это слагаемые в буквенном выражении, которые имеют одинаковую буквенную часть, а также слагаемые, которые не имеют буквенной части, если под буквенной частью понимать любое буквенное выражение.

Числовые коэффициенты подобных слагаемых могут быть равны, тогда мы говорим о том, что подобные слагаемые одинаковые. Если же числовые коэффициенты различаются, то подобные слагаемые будут разными.

Возьмем для примера выражение 2 · x · y + 3 · y · x и рассмотрим такой нюанс: являются ли слагаемые 2 · x · y и 3 · y · x подобными. В задачах этот вопрос может иметь следующую формулировку: одинаково ли буквенное выражение части x · y и y · x указанных слагаемых? Буквенные множители в приведенном примере имеют различный порядок, что в свете данного выше определения не делает их подобными.

К слову, в некоторых источниках при нестрогом отношении к вопросу, слагаемые из примера могут называться подобными. Но лучше не допускать таких неточностей в трактовках.

Приведение подобных слагаемых, правило, примеры

Под преобразованием выражений, которые содержат подобные слагаемые, подразумевается проведение сложения этих слагаемых. Проводится это действие обычно в три этапа:

Приведем пример таких вычислений.

Описанные три шага для экономии времени записывают в виде правила приведения подобных слагаемых. Согласно правило для того, чтобы привести подобные слагаемые, необходимо сложить их коэффициенты, а затем умножить полученный результат на буквенную часть при ее наличии.

Решение

Источник

Алгебра. 7 класс

Конспект урока

Стандартный вид одночлена. Подобные одночлены

Перечень рассматриваемых вопросов:

Стандартным видом одночлена называют такой его вид, в котором он представляет собой произведение числового множителя и натуральных степеней разных переменных (букв).

Подобные одночлены – это одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).

Стандартный вид нулевого одночлена – это число 0.

Правило приведения одночлена к стандартному виду:

Правило сложения (вычитания) подобных одночленов:

Коэффициент одночлена, приведенного к стандартному виду – числовой множитель одночлена.

Степенью одночлена, записанного в стандартном виде, называют сумму показателей степеней всех букв, которые входят в его запись.

Теоретический материал для самостоятельного изучения.

Известное изречение гласит: «Теория без практики – мертва, практика без теории – слепа».

И сегодня мы найдём ту «золотую середину», между теорией и практикой, при дальнейшем изучении одночленов.

Начнём с того, что введём новое понятие – стандартный вид одночлена.

Стандартный вид одночлена – это такой его вид, в котором он представляет собой произведение числового множителя и натуральных степеней разных букв. При этом каждая буква участвует в записи один раз, а все буквы записаны в алфавитном порядке.

Все представленные одночлены имеют стандартный вид, т. к. в начале одночлена стоит числовой множитель, а затем буквенные множители в алфавитном порядке.

Стоит отметить, что числовой множитель в одночленах, записанных в стандартном виде, имеет своё название – коэффициент одночлена. (Коэффициент одночлена, приведенного к стандартному виду – числовой множитель одночлена).

А одночлены 14ac 5 ax и 3k4k 2 записаны не в стандартном виде, так как числовые множители стоят не только в начале, а буквенные множители повторяются.

Стоит отметить, что стандартный вид нулевого одночлена есть число ноль.

Введём ещё одно понятие, характерное для одночленов – степень одночлена.

Степенью одночлена, записанного в стандартном виде, называется сумма показателей степеней всех букв, которые входят в его запись.

12a 2 bc 3 – одночлен 6-й степени.

xy 4 – одночлен 5-й степени

1,2cp 8 – одночлен 9-й степени

Если ни одной буквы в одночлене нет, а сам одночлен отличен от ноля, то его степень будет нулевой.

Это одночлены 0 степени.

У самого же числа 0 степень не определена, это единственный такой одночлен.

Рассмотрим правило приведения одночлена к стандартному виду.

• перемножить все числовые множители;

• поставить полученный коэффициент на первое место;

• получить буквенную часть, используя свойства степеней, так, чтобы буквы не повторялись, и были записаны в алфавитном порядке.

Привести одночлен 4ac(-3)a 2 ck к стандартному виду.

Здесь есть два числа и буквы повторяются. Найдём произведение чисел, оно равно минус двенадцати, по свойству степеней найдём степень буквы а, как сумму степеней один и два, и степень буквы c – она равна двум.

Поставим полученное числовое значение в начало, буквенные множители запишем в алфавитном порядке.

Введём ещё одно понятие – подобные одночлены.

Подобные одночлены – одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).

Для подобных одночленов можно найти сумму и разность.

Рассмотрим правило сложения (вычитания) подобных одночленов.

Чтобы сложить (вычесть) одночлены, надо:

1. составить сумму (разность), записав все одночлены один за другим;

2. привести все одночлены к стандартному виду;

3. сложить (вычесть) их коэффициенты;

4. после получившегося коэффициента дописать буквенные множители без изменений.

Если сумма (разность) коэффициентов рана нулю, то сумма (разность) одночленов равна нулю.

Например, найдём сумму (разность) подобных одночленов, используя правило.

Т. к. одночлены приведены к стандартному виду, то остаётся только найти сумму или разность их коэффициентов, а затем приписать буквенные множители.

Сумма подобных одночленов:

Разность подобных одночленов:

Итак, сегодня мы получили представление о стандартном виде одночлена и научились находить сумму и разность подобных одночленов.

Действия над одночленами.

Усложним задачу. Приведём подобные одночлены:

-(-7)aaa · (bc 2 ) 3 · (2ak) 5 + 2a 8 b 3 c 6 k 5 – 2a 7 b 3 7c 6 k 5 a

Для этого мы должны воспользоваться свойствами степеней и свойствами одночленов, рассмотренными ранее. Кроме того, нужно привести одночлены к стандартному виду, т.е. в каждом одночлене сначала записать числовой множитель, а затем буквенные в алфавитном порядке.

Возьмём первый одночлен и приведём его к стандартному виду. Произведение чисел будет равно 448. Буква а имеет 3 и 5 степень, найдём сумму этих степеней, она равна 8. Далее рассмотрим букву b, её степень находится как произведение степени 1 и 3, т.е. степень буквы b равна 3. Далее рассмотрим букву с, её степень находится как произведение степени 2 и 3, т. е. степень буквы с равна 6.

Далее рассмотрим букву k, её степень находится как произведение степени 1 и 5, т.е. степень буквы k равна 5. Итак, первый одночлен в стандартном виде выглядит так: 448a 8 b 3 c 6 k 5

Второй одночлен записан в стандартном виде.

А теперь найдём сумму и разность данных подобных одночленов.

-(-7)aaa · 2(bc 2 ) 3 · (2ak) 5 + 2a 8 b 3 c 6 k 5 – 2a 7 b 3 7c 6 k 5 a = 448a 8 b 3 c 6 k 5 + 2a 8 b 3 c 6 k 5 – 14a 8 b 3 c 6 k 5 = (448 + 2 – 14)a 8 b 3 c 6 k 5 = 436a 8 b 3 c 6 k 5

Таким образом, мы привели подобные одночлены.

Разбор заданий тренировочного модуля.

№1. Найдите одночлен, равный сумме одночленов 5ах + 2ах

Для выполнения задания нужно воспользоваться правилом сложения подобных одночленов. Для этого найдём сумму коэффициентов, а множители из букв перепишем. Получается 5ах + 2ах = (5 + 2)ах = 7ах. Это и есть правильный ответ.

Для выполнения задания, нужно вспомнить свойства степеней (при возведении в степень показатели степеней перемножаются) и правило приведения одночлена к стандартному виду (коэффициент стоит в начале одночлена, а буквы записаны в алфавитном порядке). Поэтому возведём в степень число и буквы и выстроим буквы в алфавитном порядке.

Источник

Упрощение выражений

Одно из самых распространенных заданий в алгебре звучит так: «Упростите выражение». Сделать это можно используя один из ниже перечисленных приемов, но чаще всего тебе потребуется их комбинация.

Приведение подобных слагаемых.

Для примера упростим такое выражение:

Подобные слагаемые я выделю разными цветами и посчитаю. Кстати, знак перед слагаемым относится к этому слагаемому.

Как видишь, больше одинаковых буквенных частей нет. Выражение упрощено.

Умножение одночленов и многочленов.

При умножении одночленов используют правила умножения степеней.

Перемножим три одночлена:

Разными цветами выделю то, что буду последовательно перемножать.

Чтобы умножить одночлен на многочлен выражение за скобками умножить на каждое слагаемое в скобках. Подробности в следующем примере.

Осталось вспомнить умножение многочлена на многочлен. При таком вот умножении надо каждое слагаемое в первых скобках умножить на каждое слагаемое во вторых скобках, результаты сложить или вычесть в зависимости от знаков слагаемых.

Вынесение общего множителя за скобки.

Разбираться будем на примере.

Дано такое выражение:

Что общего у этих двух слагаемых? Правильно, в них обоих присутствует множитель x. Он и будет являться общим множителем, который надо вынести за скобку.

Возьмем другой пример.

Ну и давайте третий пример, только уже без комментариев.

Проверить правильность вынесения общего множителя за скобки можно путем раскрытия скобок (умножением).

Разложение многочлена на множители способом группировки.

Если надо разложить многочлен на множители, то способ группировки тебе пригодится.

Сгруппировать выражения можно лишь путем вынесения общих множителей за скобку. Но сделать это нужно так, чтобы скобки в итоге получились одинаковые. Зачем? Да затем, чтобы потом эти скобки вынести за другие скобки.

На примере будет яснее)

Беру пример самый простой, чисто для понимания того, что надо делать.

В первых двух слагаемых общим множителем является переменная а: выносим ее за скобку. Во вторых двух слагаемых общим множителем является число 6. Его тоже выносим за скобки.

Видишь получились две одинаковые скобки? Теперь они являются общим множителем. Выносим их за скобку и получаем милое произведение двух скобок:

Разложение квадратного трехчлена на множители.

Пусть дан квадратный трехчлен:

Чтобы разложить его на множители надо решить квадратное уравнение

Далее корни уравнения х₁ и х₂ подставить в следующую формулу:

Возьмем вот такой трехчлен:

Найдем корни квадратного уравнения.

Подставим их в формулу для разложения квадратного трехчлена на множители:

Что-то слишком много минусов во второй скобке. Чуть-чуть преобразуем ее:

Еще могут тебе пригодится:

— умение сокращать дроби;

А вот такие задания могут тебе встретится на экзамене.

2) Найти значение выражения при заданных значениях переменных:

3) Найти значение выражения при заданных значениях переменных:

Источник