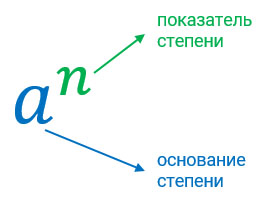
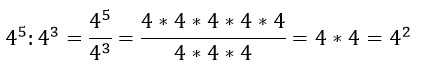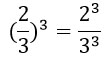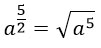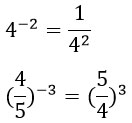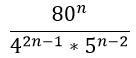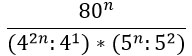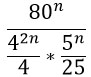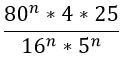Что такое показатель степени

Степени и их свойства

Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.

Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.

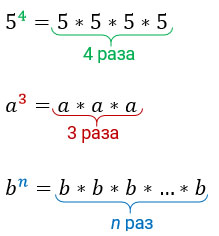
Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:

Вроде бы ничего сложного нет, правда?

Что ж, время перейти к свойствам.

Свойства степеней.

1. Любое число в первой степени равно самому себе: a 1 = a.

Сразу рассмотрим примеры.

2. Любое число в нулевой степени равно 1: а 0 = 1.

3. Единица в любой степени равна 1: 1 n = 1.

Это свойство легко доказать на числовом примере.

Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:

3 4 · 3 9 · 3 15 = 3 4 + 9 + 15 = 3 2 8 ;

Еще парочка примеров:

(2 2 ) 3 = 2 2 · 3 = 2 6 ;

8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень:.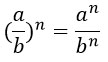

9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле 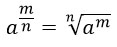(а > 0, n ≥ 2).

10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: 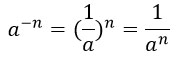(a ≠ 0).

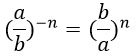
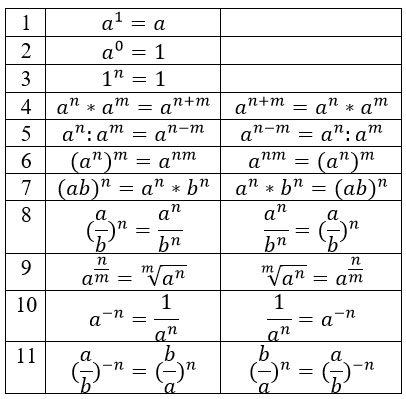
Это же правило работает и для дробей: (a ≠ 0, b ≠ 0).

Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.

Нам нужно сократить такую дробь:

Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.

Получившиеся частные в знаменателе запишем в виде дробей.

Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂

Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!

Источник

Степень числа

Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.

Рассмотрим умножение одинаковых чисел, например:

Произведение 5 · 5 · 5 можно записать так: 5 3 (пять в третьей степени). Выражение 5 3 — это степень. Следовательно,

Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.

Читаются степени так:

Пример. Записать в виде степени:

б) 10 · 10 · 10 · 10 = 10 4 ;

Возведение в степень

Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:

2 — это основание степени, 3 — показатель степени, 8 — степень.

a) 11 2 = 11 · 11 = 121;

б) 2 5 = 2 · 2 · 2 · 2 · 2 = 32;

в) 10 4 = 10 · 10 · 10 · 10 = 10000.

Выражения со степенями. Порядок действий

Если выражение не содержит скобки и содержит степени, то сначала выполняется возведение в степень в порядке следования степеней (слева направо), а затем все остальные арифметические действия. Если выражение содержит скобки, то сначала выполняются действия в скобках, с учётом всех правил порядка выполнения действий.

Рассмотрим два выражения:

В соответствии с порядком выполнения действий в первом случае сначала выполняется возведение в степень, а затем вычисляется сумма. Во втором случае сначала вычисляется сумма, а затем результат возводится в квадрат.

5 2 + 2 2 = 25 + 4 = 29,

Пример 1. Найти значение выражения:

Решение: Сначала выполняется действие, заключённое в скобки:

Затем, по правилам порядка действий, выполняется возведение в степень:

И последним действием вычисляется произведение:

Пример 2. Вычислить:

Калькулятор возведения в степень

Источник

Что такое степень числа

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Исключение составляют записи:

Конечно, выражения выше можно читать и по определению степени:

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Квадрат любого числа есть положительное число или нуль, то есть:

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

Пример. Вычислить: −6 2 − (−1) 4

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Источник

Свойства степеней. Действия со степенями

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

a — основание степени;

n — показатель степени.

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).

Источник

Числа. Степень числа.

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

В общем виде степень с основанием «a» и показателем «n» записывается так

Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а

Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1

Если возвести число «а» возвести в первую степень, то получим само число a: a 1 = a

Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа, третью – кубом этого числа.

-при нахождении степени положительного числа получается положительное число.

-при вычислениях нуля в натуральной степени получаем ноль.

— при вычислении степени отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Если решить несколько примеров на вычисление степени отрицательных чисел, то получится, что если мы вычисляем нечётную степень отрицательного числа, то в результате будет число со знаком минус. Так как при умножении нечётного количество отрицательных сомножителей получаем отрицательное значение.

Если же мы рассчитываем четную степень для отрицательного числа, то в результате будет положительное число. Так как при умножении чётного количества отрицательных сомножителей получаем положительное значение.

Свойства степени с натуральным показателем.

Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:

Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:

При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.

например: (2 3 ) 2 = 2 3·2 = 2 6

Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель

При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби

Последовательность выполнения расчетов при работе с выражениями содержащими степень.

При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.

Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.

Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.

Источник