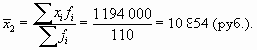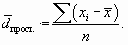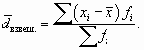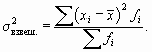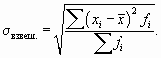Что такое показатели вариации и для чего они вычисляются

Показатели вариации и способы их расчета

Понятие вариации

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называются факторами. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности. Но есть и несущественные (случайные), которые на одни единицы совокупности могут оказывать влияние, на другие нет.

Вариация, обусловленная случайными факторами, называется случайной вариацией. Здесь не наблюдается систематического изменения вариантов зависимого признака от случайных факторов; все изменения носят хаотический характер, поскольку нет устойчивой связи этих факторов с единицами изучаемой совокупности.

Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Следовательно, общая вариация слагается из систематической и случайной вариации. Но систематическая вариация, если между признаками имеется довольно существенная связь, в конце концов пробивает себе дорогу через хаос случайных колебаний вариантов зависимого признака и проявляет себя.

Показатели вариации и способы их расчета

Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание, рассеяние значений признака. Исчислив среднюю арифметическую по данным вариационного ряда, мы не знаем о том, как отдельные значения изучаемого признака группируются вокруг средней. Для вариационного ряда важно изучать степень сплоченности всех отдельных значений признака вокруг его среднего значения, степень разбросанности этих значений, степень их колеблемости. Для этого в теории статистики используются показатели вариации.

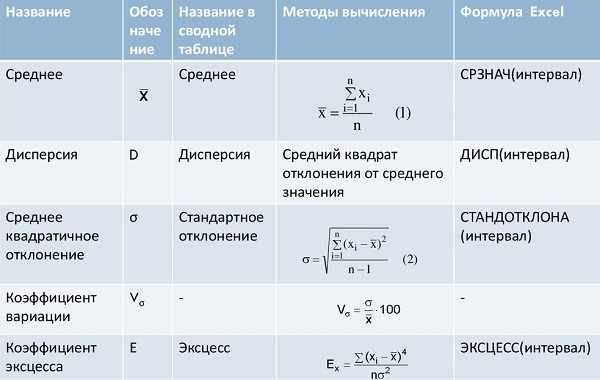
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. К относительным показателям вариации относятся: коэффициенты вариации, осцилляции, относительное линейное отклонение и др. Относительные показатели вычисляются как отношение абсолютных показателей вариации к средней величине.

1.Размах вариации (R)представляет собой разность между максимальным (x_max) и минимальным (x_min) значением признака исследуемой совокупности:

.

Размах вариации (амплитуда колебаний) дает лишь самое общее представление о размерах вариации, характеризует предел изменения значений признака в исследуемой совокупности. Этот показатель вариации обладает существенным недостатком: он характеризует только отклонения и не дает представление о распределении отклонений по все совокупности. Его величина определяется двумя крайними значениями признака, в то время как колеблемость последнего в целом складывается из всех его значений. Для анализа вариации необходим показатель, который бы отражал все колебания варьирующего признака и давал обобщенную его характеристику.

2. Среднее линейное отклонение ( 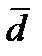)– это среднее из абсолютных отклонений значений признака от средней арифметической:

, .

Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю.

Таково в среднем линейное отклонение вариантов признака от их средней величины. Если среднее линейное отклонение по сравнению со средней величиной признака небольшое, это свидетельствует о том, что данная совокупность в отношении нашего признака однородна, а средняя – типична. Таким образом, среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности.

3. Дисперсия – это среднее из квадратов отклонений индивидуальных значений признака от средней величины:

, .

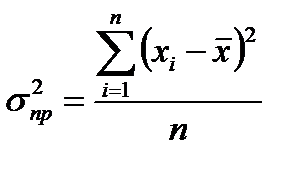
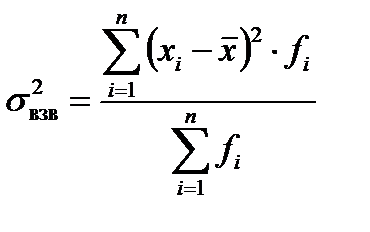
Математические свойства дисперсии

1) Дисперсия постоянной величины равна нулю:

.

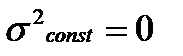
2) Дисперсия не изменится, если все значения признака увеличить или уменьшить на некоторую постоянную величину А.

.

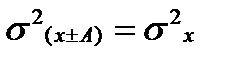
3) Если все значения варьирующего признака разделить (умножить) на одну и ту же величину h, то дисперсия уменьшится (увеличится) в h 2 раз.

, .

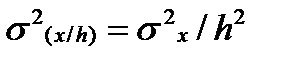
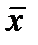
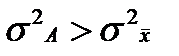
4)Средний квадрат отклонений индивидуальных значений признака от любой величины А, отличающейся от средней арифметической (A ≠ ), всегда больше среднего квадрата отклонений, исчисленного от средней арифметической:

или .

Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней от этой условно взятой величины А, т.е. на .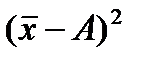

Другими словами, дисперсия от средней имеет свойство минимальности, т.е. она всегда меньше дисперсий, исчисленных от любых других величин.

или .

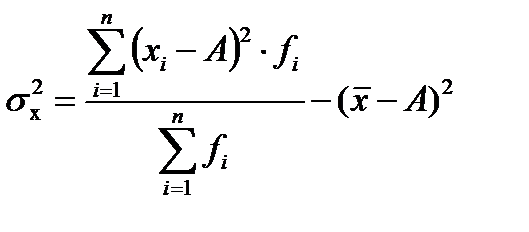
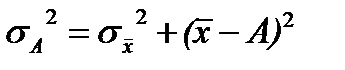
В случае когда А приравнивается нулю и, следовательно, отклонения не вычисляются, формула принимает следующий вид:

, или .

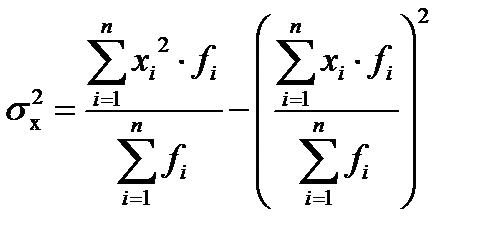
4.Среднее квадратическое отклонение находится как корень из дисперсии. Показывает (как и среднее линейное отклонение) на сколько в среднем индивидуальные значения признака отклоняются от средней арифметической:

, .

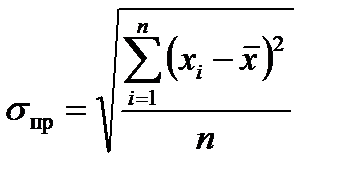
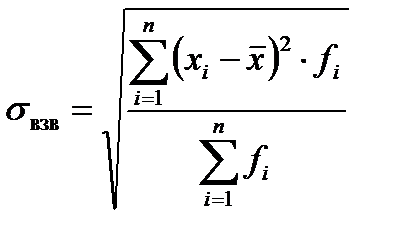
5.Коэффициент вариации – это относительный показатель, исчисляемый как отношение среднего квадратического отклонения к средней арифметической:

.

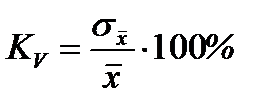
Считается, что если коэффициент вариации превышает 33%, то совокупность нельзя признать качественно однородной. Если K_v ≤ 33%, то можно утверждать, что совокупность более или менее однородна, а следовательно, средняя, рассчитанная по такой совокупности, типична. Необходимость исчисления коэффициента вариации вызвана тем, что показатели вариации в абсолютных величинах, как правило, непосредственно несравнимы.

Пример. Рассчитать показатели вариации по имеющимся данным (табл. 8.1).

Таблица 8.1 – Распределение предприятий по объему продаж

Группа предприятий по объему продаж, млн.руб.	Число предприятий в группе
1-5
5-9
9-13
13-17
17-21
ИТОГО

Алгоритм расчета показателей вариации следующий:

1) определим размах вариации:

R = 21 – 1 = 20 млн. руб.

2) найдем середину интервалов по исходным данным (x_i) и запишем в табл. 8.2;

3) определим среднее значение по формуле средней арифметической взвешенной, для этого введем графу (x_i f_i):

млн. руб.

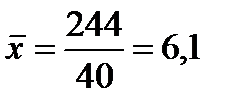
4) для расчета среднего линейного отклонения введем графы и :

млн. руб.

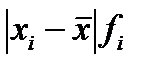
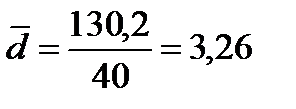
Таково в среднем отклонение вариантов признака от их средней величины.

5) для расчета дисперсии введем графы и :

.

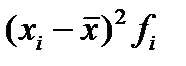
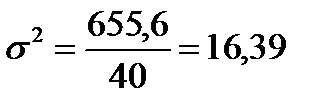
6) рассчитаем дисперсию упрощенным способом, для этого введем графу ( ):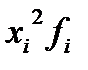

.

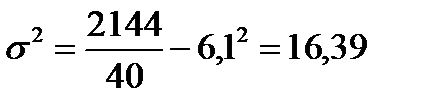
7) извлечем из дисперсии корень и получим среднее квадратическое отклонение:

млн. руб.

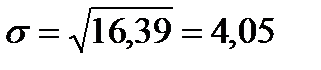
8) определим коэффициент вариации:

или 66%.

K_v > 33%, следовательно, изучаемая совокупность качественно неоднородна и рассчитанное среднее значение нетипично.

Таблица 8.2 – Расчет показателей вариации

Группа предприятий по объему продаж, млн.руб.	Число предприятий в группе, fi	Середина интервала, xi	xi fi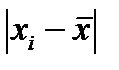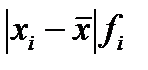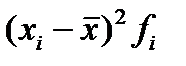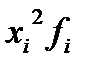
1-5	3,1	65,1	9,61	201,81
5-9	0,9	9,9	0,81	8,91
9-13	4,9	24,5	24,01	120,05
13-17	8,9	17,8	79,21	158,42
17-21	12,9	12,9	166,41	166,41
ИТОГО	—	—	130,2	—	655,6

Дата добавления: 2015-12-26 ; просмотров: 11576 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Вариация понятие, относительные и абсолютные показатели, способы их расчета

Этот термин ведёт своё происхождение от латинского слова «varito». Оно переводится как «изменение» или «различие».

Вариация это количественная мера изменения определённых данных, которая помогает исследовать её случайные изменения. Для их анализа применяют различные статистические методы.

О них будет более подробно рассказано в этой статье.

Онлайн-калькулятор показателей вариации

Показатели вариации в статистике

Статистика широко применяется в самых различных областях. Она доказала свою пользу не только в естественных науках, но и в изучении различных социологических явлений, изменений цен, а также в других ситуациях.

Эта наука имеет дело со случайными величинами, изменение которых требует для своего описания использования специальных характеристик. Наиболее известной из них является средняя. Однако, хотя она и включает в себя некоторый объём информации, тем не менее не даёт возможности найти информацию о разбросе случайных данных, а также дать понятие о динамике изменения и наиболее вероятных тенденциях в дальнейшем.

Математический аппарат для изучения вариационных процессов использует характеристики, способы расчёта которых можно разделить на три группы.

Показатели размаха изменений говорят о том, какова разница между максимальными отклонениями исследуемых чисел:

Данные, относящиеся ко второй категории, можно считать так:

Для расчёта относительных показателей применяется:

Далее будет рассказано о наиболее часто применяемых математических характеристиках рассматриваемого понятия.

При проведении статистических вычислениях удобно пользоваться электронными таблицами Excel.

Абсолютные показатели вариации

Когда говорят об абсолютных показателях вариации, имеют в виду следующие методы для проведения статистического анализа:

Размах вариации

При рассмотрении изменения исследуемых данных, одной из важных характеристик является размах вариации.

Он равен разности между максимальной и минимальной границами. Посмотрим, как это характеристика исчисляется.

Формула выглядит так:

РВар = ЗнМакс — ЗнМин,

Пример.

Эта формула может быть применена, например, в следующей ситуации. Предположим, рассматривается рост отобранных случайным образом людей. В этой совокупности десять человек и рост их равен: 165, 172, 179, 190, 182, 171, 191, 183, 177 и 178 сантиметров. Эти цифры составляют совокупность значений случайных данных.

Как можно увидеть в рассматриваемом случае, минимальный рост в этой группе людей составляет 165 см, а максимальный — 191 см. Разница между ними составляет 191 — 165 = 26 см. Таким образом, рассматриваемое значение для определённой таким образом совокупности данных показывает 26 см.

Отклонение вариации

Здесь рассматривается отклонение изучаемой случайной величины. Для того, чтобы его вычислить, необходимо сначала определить её среднее значение.

Чтобы посчитать, необходимо просуммировать все значения случайных данных и затем разделить на их количество. Получившаяся величина представляет собой нужный результат.

В некоторых формулах используются значения весов, придаваемых каждому значению. Кратко говоря, они назначаются в соответствии с целями проведения статистического исследования. Веса обычно подбираются таким образом, чтобы их сумма была равна единице.

Среднее линейное простое

Оценка величины отклонения рассчитывается так:

Формула выглядит таким образом:

СЛП = (|x(1) – x0| + |x(2) – x0| + … + |x(n) – x(0)|) / n,

Вертикальные чёрточки используются для того, чтобы показать, что здесь вычисляется абсолютная разность.

Среднее линейное взвешенное

Для этого потребуется формула:

СЛВ = (|x(1) – x0|*f(1) + |x(2) – x0|*f(2) + … + |x(n) – x(0)|*f(n)) / n,

Остальные обозначения рассмотрены ранее.

Среднее квадратическое отклонение

В этом случае результат определяется по другому правилу, чем в прежних случаях:

СКО = SQRT(((x(1) – x0)**2 + (x(2) – x0)**2 + … + (x(n) – x(0))**2) / n),

Дисперсия (простая, взвешенная)

Простая дисперсия равна СКО, возведённому в квадрат.

Взвешенная называется так потому, что каждое слагаемое умножается на свой вес.

Здесь применяется формула:

ДВ = (f(1)*(x(1) – x0)**2 + f(2)*(x(2) – x0)**2 + … + f(n)*(x(n) – x(0))**2) / n*(f(1) + f(2) + … + f(n)),

где: ДВ представляет собой дисперсию взвешенную.

Вариация альтернативного признака

Это понятие характеризует те ситуации, когда часть предметов выборки обладает определённым свойством, а другая — нет:

СРЕД = ((1-p) + (0-p)) / (p+q) = p,

ВАР = (q*(1-p)**2+ q*(0-p)**2) / (p+q) = pq.

Здесь СРЕД обозначает среднее, а p и q представляют собой положительные числа, в сумме дающие единицу.

ВАР обозначает искомую величину.

Относительные показатели вариации

В данном случае рассматриваются отношение отклонения и среднего конкретной выборки. Для различных характеристик используются различные способы определения среднего отклонения.

Чем меньше полученный коэффициент, тем более сгруппированы данные. Этот коэффициент не имеет единиц измерения.

Коэффициент осцилляции

Эта величина равна частному от деления размаха вариации на среднее случайной величины.

Коэффициент вариации

Такой коэффициент можно рассчитать путём деления линейного отклонения на такой же знаменатель, как в предыдущем случае.

Относительное линейное отклонение

В данном случае искомое значение рассчитывается как результат деления среднего квадратического на этот же знаменатель.

Примеры расчетов

Здесь будет приведены примеры расчётов. Рассматривается ситуация, когда пять человек устраиваются на новую работу. В данной специальности они проработали различное количество лет: 2, 3, 4, 7 и 9 лет.

X(0) = (2 + 3 + 4 + 7 + 9) / 5 = 25 / 5 = 5.

СЛП = (|x(1) – x0| + |x(2) – x0| + … + |x(n) – x(0)|)/n = (|2 5| + |3 5| + |4 5| + |7 5| + |9 – 5|) / 5 = (3 + 2 + 1 + 2 + 4) / 5 = 12 / 5 = 2,4 года.

СКО = SQRT(((x(1) – x0)**2 + (x(2) – x0)**2 + … + (x(n) – x(0))**2)/n) = SQRT(((2 – 5)**2 + (3 – 5)**2 + (4 – 5)**2 + (7 – 5)**2 + (9 – 5)**2) / 5) = SQRT((3**2 + 2**2 + 1**2 + 2**2 + 4**2)/5) = SQRT ((9 + 4 + 1 + 4 + 16) / 5) = SQRT(34 / 5) = SQRT(6,80) = 2,61 года (приблизительное значение).

Последнее значение равно СКО, возведённому в квадрат.

В большинстве случаев расчет представляет собой гораздо более сложную задачу, чем показано в приведённом примере. Для облегчения процесса вычислений можно использовать онлайн калькулятор.

Заключение

Изучение случайных процессов играет важную роль в науке, экономике и общественной жизни. Для того, чтобы получить максимальное количество информации при их изучении, нужно активно использовать статистические методы, в том числе те, которые связаны с вариацией.

Источник

Показатели вариации

Классификация показателей вариации

Числовые характеристики вариационного ряда

Относительные показатели вариации

Рассмотрим показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Чаще всего относительные показатели выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
Различают следующие относительные показатели вариации (V):
Коэффициент осцилляции (V_R): .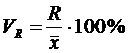

Линейный коэффициент вариации (V):
.
Коэффициент вариации (V_σ): .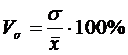

Решение. В разделе «Вид статистического ряда» выбираем Интервальный ряд (рис. 1).

3. На странице ввода данных заполняем исходные данные (рис. 2). При этом открытые интервалы корректируем на закрытые: из открытого интервала «до 3» формируем закрытый 3, из интервала «15 и более» создаем интервал 16.

По умолчанию в отчет включается расчет следующих показателей вариации:
средняя взвешенная, мода, медиана, абсолютные показатели вариации (размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение), относительные показатели вариации (коэффициент вариации, линейный коэффициент вариации).

Примечание: несмещенная оценка дисперсии и оценка среднеквадратического отклонения используются при проверке гипотезы о виде распределения, определении относительной ошибки выборки, и в случаях, когда это непосредственно требуется в задании. Во всех остальных случаях данные показатели можно исключить из отчета.

Расчет показателей вариации

Типы вариации

Меры вариации

Вариация существует и в пространстве и во времени.
Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям.
Под вариацией во времени подразумевают изменение значений признака в различные моменты времени. Так, со временем изменяются средняя продолжительность жизни, мнения людей и т.д.
Показатели вариации делятся на две группы: абсолютные и относительные.

К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднеквадратическое отклонение. Вторая группа показателей вычисляется, как отношение абсолютных показателей к средней арифметической (медиане).

Прежде, чем определить величину размаха вариации необходимо очистить совокупность от аномальных наблюдений.
Например, нельзя вычислять размах вариации работников какого-либо частного предприятия, если наряду с заработками его работников включен заработок его владельца.
Размах вариации – важный показатель колеблемости признака, но не исчерпывающий его характеристику.

Рассмотрим среднее линейное отклонение. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант x_i от по формуле:

(простая средняя),

(взвешенная средняя).

Источник

Показатели вариации в статистике

7.1. Абсолютные и относительные показатели вариации

Рассмотрим две совокупности сотрудников рекламных агентств.

Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.

Таблица 7.1. Распределение сотрудников первого агентства по уровню месячной заработной платы

Размер месячной заработной платы, руб.	Середина интервала, xi	Число сотрудников, чел., fi	xi*fi
4 000-6 000	5 000	10	50 000
6 000-8 000	7 000	6	42 000
8 000-10 000	9 000	19	171 000
10 000-12 000	11 000	26	286 000
14 000-16 000	15 000	10	150 000
16 000-18 000	17 000	5	85 000
Сумма	—	95	1 031 000

Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.

Таблица 7.2. Распределение сотрудников второго агентства по уровню месячной заработной платы

Размер месячной заработной платы, руб.	Середина интервала, xi	Число сотрудников, чел., fi	xi*fi
1 500-4 500	3 000	9	27 000
4 500-7 500	6 000	26	156 000
7 500-10 500	9 000	24	216 000
10 500-13 500	12 000	18	216 000
13 500-16 500	15 000	14	210 000
16 500-19 500	18 000	10	180 000
19 500-22 500	21 000	9	189 000
Сумма	—	110	1 194 000

Рассчитаем средний уровень заработной платы:

Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.

Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.

Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака

( 7.1)

Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение

( 7.2)

Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:

( 7.3)

Дисперсией (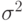) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней

( 7.4)

( 7.5)

Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением):

( 7.6)

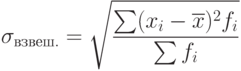( 7.7)

Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:

Источник