Что такое поликоническая проекция
Что такое поликоническая проекция
Рис 13. Картографическая сетка в псевдоконической проекции
Точка зрения и картинная плоскость могут занимать самое различное положение относительно центра шара или эллипсоида. По виду меридианов и параллелей нормальной сетки эти проекции ничем не отличаются от азимутальных проекций.
Псевдоконическими называются такие проекции, в которых параллели нормальной сетки изображаются дугами концентрических окружностей, а меридианы — кривыми линиями, симметричными относительно среднего меридиана, который изображается прямой, перпендикулярной к параллелям. Эти проекции отличаются, от конических видом меридианов. Вид картографической сетки псевдоконической проекции показан на рис. 13.
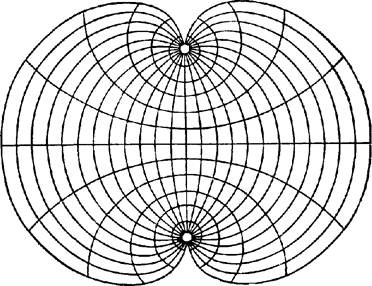
В псевдоконических проекциях линиями нулевых искажений являются средний меридиан и средняя параллель. Искажения в них нарастают по мере удаления от этих линий. Вид изокол углов в этих проекциях показан на рис. 14.
Псевдоконические проекции применяются при изображении территорий, имеющих форму ромба с вогнутыми сторонами.
Рис 14. Изоколы углов в псевдоконической проекции.
Псевдоцилиндрическими называются такие проекции, в которых параллели нормальной сетки изображаются параллельными прямыми, а меридианы — кривыми линиями, симметричными относительно среднего меридиана, который изображается прямой, перпендикулярной к параллелям. Эти проекции отличаются от цилиндрических видом меридианов. В псевдоцилиндрических проекциях изоколы имеют вид сложных кривых линий, симметричных относительно экватора и среднего меридиана, причем закон нарастания искажений может быть различным.
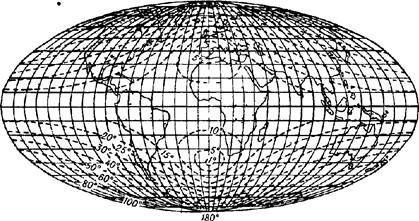
На рис. 15 показан вид картографической сетки и изокол углов в одной из равновеликих псевдоцилиндрических проекций (проекции Мольвейде), в которой углы не искажаются только в точках пересечения среднего меридиана с параллелями 40°44′ северной и южной широты.
При изображении всего земного шара эти проекции дают меньшие искажения, чем цилиндрические.
Поликонические проекции
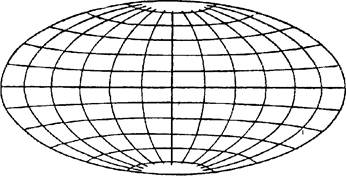
Поликоническими называются такие проекции, в которых параллели нормальной сетки изображаются разноцентренными окружностями, а меридианы — кривыми линиями, симметричными относительно среднего меридиана, который изображается прямой, перпендикулярной к параллелям.
Поликонические проекции можно рассматривать, как проекции глобуса не на один касательный по параллели конус, а на множество касательных конусов, что обусловливает равенство масштабов
Рис 15 Картографическая сетка и изоколы углов в псевдоцилиндрической
Проекции по всем параллелям. В этих проекциях масштаб по всем параллелям и на среднем меридиане равен единице. Искажения возрастают с удалением от среднего меридиана, и изоколы имеют вид линий, приблизительно параллельных среднему меридиану. Поэтому эти проекции более выгодно применять для изображения территорий, сильно
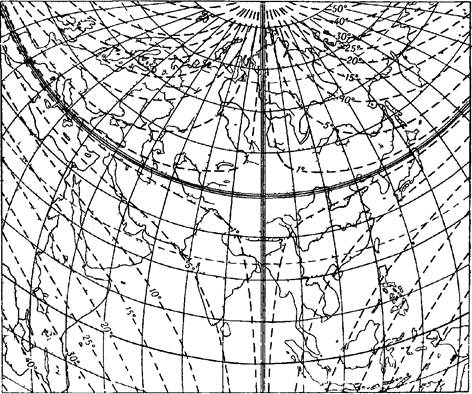
Рис 16 Картографическая сетка в поликонической проекции
вытянутых вдоль меридианов хотя бы от одного полюса до другого. Вид, картографической сетки в поликонической проекции показан на рис. 16.
Частным случаем поликонических проекций являются круговые проекции. Круговыми называются такие проекции, в которых средний меридиан и экватор нормальной сетки изображаются прямыми перпендикулярными линиями, а остальные меридианы и параллели—дугами разноцентренных окружностей, причем средний меридиан является осью симметрии для остальных меридианов, а экватор — осью симметрии для параллелей.
К прочим относятся такие проекции, которые не могут быть отнесены ни к одному из рассмотренных выше классов проекций по виду меридианов и параллелей нормальной сетки. Меридианы и параллели в них изображаются весьма разнообразно. Изоколы в этих проекциях обычно имеют вид сложных кривых линий, симметрично расположенных относительно экватора и среднего меридиана.
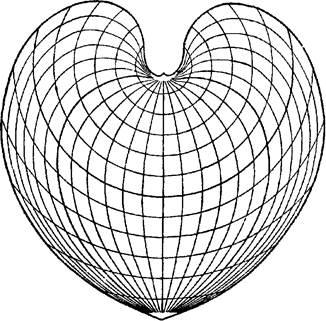
Рис. 17. Картографическая сетка в проекции Аитова-Гаммера.
Эти проекции нашли широкое применение для мировых карт. Вид картографической сетки одной из этих проекций (проекция Аитова-Гаммера) показан на рис.17
Поликонические проекции
Смотреть что такое «Поликонические проекции» в других словарях:
ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ — картографические проекции, параллели которых дуги эксцентрических окружностей, а меридианы кривые, симметричные относительно среднего прямолинейного меридиана. Применяются для карт мира … Большой Энциклопедический словарь
поликонические проекции — картографические проекции, параллели которых дуги эксцентрических окружностей, а меридианы кривые, симметричные относительно среднего прямолинейного меридиана. Применяются для карт мира. * * * ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ,… … Энциклопедический словарь
ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ — картографии проекции, параллели к рых дуги эксцентрич. окружностей, а меридианы кривые, симметричные относительно ср. прямолинейного меридиана. Применяются для карт мира … Естествознание. Энциклопедический словарь
Картографические проекции — отображения всей поверхности земного эллипсоида (См. Земной эллипсоид) или какую либо её части на плоскость, получаемые в основном с целью построения карты. Масштаб. К. п. строятся в определённом масштабе. Уменьшая мысленно… … Большая советская энциклопедия
картографические проекции — математические способы изображения на плоскости поверхности земного эллипсоида или шара. Картографические проекции определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть… … Энциклопедический словарь
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ — математические способы изображения на плоскости поверхности земного эллипсоида или шара. Картографические проекции определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть… … Большой Энциклопедический словарь
Картографическая проекция — Пример картографической проекции проекция Меркатора Картографическая проекция математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли … Википедия
Проекция (картография) — Пример картографической проекции проекция Меркатора Картографическая проекция математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли эллипсоид, не развертываемый в… … Википедия
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — отображение всей поверхности земного эллипсоида или какой либо ее части на плоскость, получаемое в основном с целью построения карты. К. п. чертят в определенном масштабе. Уменьшая мысленно земной эллипсоид в Мраз, получают его геометрич. модель… … Математическая энциклопедия
Справка
Описание
Название проекции переводится как «много конусов». Это влияет на форму меридианов. Это относится к методу проецирования. В отличие от других конических проекций, меридианы отображаются дугами, а не прямыми линиями.
Метод проецирования
Более сложное, чем в обычной конической проекции, но все равно довольно простое построение. Эта проекция создана ‘склеиванием‘ бесконечного числа конусов вдоль центрального меридиана. В этой проекции параллели не являются концентрическими. Каждая линия широты соответствует основе касательного конуса.
Линии контакта
Много линий; все параллели проекции.
Линейные элементы картографической сетки
Центральный меридиан проекции и экватор.
Свойства
Форма
Нет искажений форм местности вдоль центрального меридиана. Искажения увеличиваются по мере удаления от центрального меридиана; таким образом, искажения в направлении восток-запад больше, чем искажения в направлении север-юг.
Площадь
Искажения площадей увеличиваются по мере удаления от центрального меридиана.
Направление
Местные углы являются точными вдоль центрального меридиана; в противном случае, они искажены.
Расстояние
Масштаб вдоль каждой параллели и вдоль центрального меридиана проекции является точным. Искажения увеличиваются вдоль меридианов по мере удаления от центрального меридиана.
Ограничения
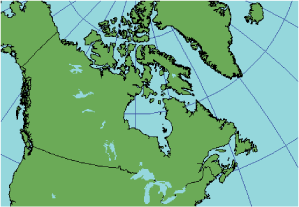
Искажения минимизированы на крупномасштабных картах, таких как листы топографических карт, на которых сегменты меридианов и параллелей могут быть изображены прямыми отрезками. Создание библиотеки карт из таких листов не рекомендуется, поскольку происходит накопление ошибок, которое становится видимым при соединении листов в нескольких направлениях.
Области использования
ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ
Смотреть что такое «ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ» в других словарях:
поликонические проекции — картографические проекции, параллели которых дуги эксцентрических окружностей, а меридианы кривые, симметричные относительно среднего прямолинейного меридиана. Применяются для карт мира. * * * ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ,… … Энциклопедический словарь
Поликонические проекции — один из видов картографических проекций (См. Картографические проекции) … Большая советская энциклопедия
ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ — картографии проекции, параллели к рых дуги эксцентрич. окружностей, а меридианы кривые, симметричные относительно ср. прямолинейного меридиана. Применяются для карт мира … Естествознание. Энциклопедический словарь
Картографические проекции — отображения всей поверхности земного эллипсоида (См. Земной эллипсоид) или какую либо её части на плоскость, получаемые в основном с целью построения карты. Масштаб. К. п. строятся в определённом масштабе. Уменьшая мысленно… … Большая советская энциклопедия
картографические проекции — математические способы изображения на плоскости поверхности земного эллипсоида или шара. Картографические проекции определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть… … Энциклопедический словарь
КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ — математические способы изображения на плоскости поверхности земного эллипсоида или шара. Картографические проекции определяют зависимость между координатами точек на поверхности земного эллипсоида и на плоскости. Из за невозможности развернуть… … Большой Энциклопедический словарь
Картографическая проекция — Пример картографической проекции проекция Меркатора Картографическая проекция математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли … Википедия
Проекция (картография) — Пример картографической проекции проекция Меркатора Картографическая проекция математически определенный способ отображения поверхности эллипсоида на плоскости. Суть проекций связана с тем, что фигуру Земли эллипсоид, не развертываемый в… … Википедия
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — отображение всей поверхности земного эллипсоида или какой либо ее части на плоскость, получаемое в основном с целью построения карты. К. п. чертят в определенном масштабе. Уменьшая мысленно земной эллипсоид в Мраз, получают его геометрич. модель… … Математическая энциклопедия
ArcMap
Описание
Название проекции переводится как «много конусов». Это влияет на форму меридианов. Это относится к методу проецирования. В отличие от других конических проекций, меридианы отображаются дугами, а не прямыми линиями.
Метод проецирования
Более сложное, чем в обычной конической проекции, но все равно довольно простое построение. Эта проекция создана ‘склеиванием‘ бесконечного числа конусов вдоль центрального меридиана. В этой проекции параллели не являются концентрическими. Каждая линия широты соответствует основе касательного конуса.
Линии контакта
Много линий; все параллели проекции.
Линейные элементы картографической сетки
Центральный меридиан проекции и экватор.
Свойства
Форма
Нет искажений форм местности вдоль центрального меридиана. Искажения увеличиваются по мере удаления от центрального меридиана; таким образом, искажения в направлении восток-запад больше, чем искажения в направлении север-юг.
Площадь
Искажения площадей увеличиваются по мере удаления от центрального меридиана.
Направление
Местные углы являются точными вдоль центрального меридиана; в противном случае, они искажены.
Расстояние
Масштаб вдоль каждой параллели и вдоль центрального меридиана проекции является точным. Искажения увеличиваются вдоль меридианов по мере удаления от центрального меридиана.
Ограничения
Искажения минимизированы на крупномасштабных картах, таких как листы топографических карт, на которых сегменты меридианов и параллелей могут быть изображены прямыми отрезками. Создание библиотеки карт из таких листов не рекомендуется, поскольку происходит накопление ошибок, которое становится видимым при соединении листов в нескольких направлениях.