Что такое политропная мощность нагнетателя
Оптимизация режимов работы газоперекачивающих агрегатов с газотурбинным приводом по условию максимального КПД
Одной из наиболее важных задач в условиях использования газотурбинного энергопривода на газопроводах является задача обеспечения наиболее экономичных режимов работы ГПА при перекачке заданного количества газа, что всегда связано с экономией топливного газа по станции.
n = n0 
Изменение частоты вращения вала нагнетателя (Рис. 5.14) осуществляется до величины 3250 с интервалом между рассматриваемыми характеристиками 250 об./мин. и весьма наглядно показывает как изменяется относительный КПД нагнетателя при изменении подачи газа и частоты вращения его вала.
Естественно, что при рассмотрении характеристики нагнетателя в достаточно широком диапазоне изменения частоты вращения его вала, необходимо выдерживать условие работы нагнетателя в допустимой зоне работы, nmin £ n £ nmax. [16].
Рассмотрение данных Рис. 5.14 показывает, что значительный перерасход топливного газа на величину 3-6 % связан с характером зависимости hпол. = f (Qпр.), характеризующей резкое падение КПД нагнетателя по краям этой характеристики.
Для достижения максимального политропного КПД нагнетателя необходимо выдерживать оптимальные режимные значения e, Q и n, соответствующие hпол. = max, которые не всегда соответствуют оптимальным значениям по этой зависимости (Рис. 5. 14) и что связано с несогласованностью характеристик нагнетателя и газопровода.
Результаты эксплуатационных данных показывают, между изменением в расходе топливного газа по ГПА и политропгым КПД нагнетателя существует следующая простая зависимость [14]:
Полученное соотношение показывает, насколько важно в условиях эксплуатации обеспечить условие работы нагнетателей на режимах hпол. = max. Уравнение (5.24) показывает, что снижение численного значения КПД нагнетателя только на 1% приводит к перерасходу топливного газа на 1,1%.
Выбор оптимальной частоты вращения вала нагнетателя, осуществляемый по условию hпол. = max. в практических условиях может быть проведен по предварительному определению диапазона изменения подачи газа по нагнетателю по его характеристике в зоне наивысшего значения КПД нагнетателя.
Соответственно может быть определено и соотношение давлений сжатия по первому нагнетателю (в условиях двухступенчатого сжатия) по условию hпол. = max. [16]:

Второй последовательно работающий в группе агрегат также должен работать при максимальном значении политропного КПД. Его объемная производительность в этом случае будет определяться соотношением:
Q2 = Q1 
Оптимальная частота вращения для этой производительности, а также соотношение давлений сжатия определяются по следующим соотношениям:
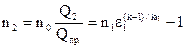
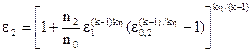
При использовании полнонапорных нагнетателей в качестве расчетного уравнения используется практически только уравнение (5.25).
С учетом приведенных соотношений, оптимальная зона работы нагнетателя типа 370-18-1 по условию максимального КПД ГТУ будет характеризоваться данными Рис. 5.15.
Значительный интерес всегда представляет совмещение характеристик нагнетателя и ГТУ с целью оценки совпадения значений их максимальных КПД. Решение этой задачи начинается прежде всего с определения мощности, потребляемой нагнетателем, при которой выполняется условие hпол. = max.
Определение мощности, потребляемой нагнетателем, можно осуществить с использованием известных формул приведения (для двухступенчатого сжатия):


При использовании полнонапорных нагнетателей расчетные соотношения несколько упрощаются и для определения мощности можно использовать только соотношение (5.29).
Переход к характеристикам газотурбинной установки осуществляется по условию равенства мощностей нагнетателя и ГТУ, Nе,ГТУ = Ni,наг. + Nмех., где Nмех. – механические потери мощности в системе соединения турбины и нагнетателя.
Зависимость эффективного КПД ГТУ от ее мощности определяется соотношением:

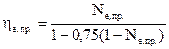
Результаты совмещения характеристик нагнетателя и газовой турбины с учетом соотношений (5.2 и 5.25-5.31) приведены на Рис. 5.16.
Приведенная номограмма совмещения оптимальных режимов работы ГПА по условиям максимального значения КПД нагнетателя и ГТУ дает возможность при заданной производительности нагнетателя в первом приближении определять и оптимальную температуру газов перед турбиной высокого давления, при которой КПД также будет иметь максимальное значение.
Приведенная относительная мощность установки от приведенной температуры газов перед газовой турбиной в первом приближении определяется соотношением [6]:
В условиях, когда температуру газов перед ТВД определить сложно, ее можно определить расчетным путем по известной температуре газов за ТНД.
Следует отметить, что аналогичным образом могут быть построены номограммы и для других типов ГПА с другими нагнетателями и другими типами газотурбинных установок.
Приведенная относительная температура газов за ТНД в зависимости от приведенной мощности установки в первом приближении может быть определена по соотношению:
Наличие уравнений (5.32) и (5.33) позволяет легко построить графические зависимости между переменными, входящими в эти соотношения для различных режимов работы и по ним судить как изменяются эти одни из основных параметров ГТУ в процессе эксплуатации.
Решение. Решение данной задачи осуществляется в следующей последовательности: вначале оценивается техническое состояние нагнетателя, затем определяется потребляемая им мощность и подача газа. Найденная величина мощности используется как для определения технического состояния газотурбинной установки, так и для определения расхода топливного газа и эффективного КПД самой ГТУ.
Средние значения температуры и давления в процессе сжатия:
Средняя изобарная теплоемкость любого природного газа в процессе сжатия может быть определена по следующему эмпирическому соотношению в зависимости от процентного содержания метана в газе и параметров процесса сжатия [ ], В данном примере ее можно принять равной Сpm = 2,17 кДж/кг 0 С.
Для определения реальной удельной работы сжатия газа в нагнетателе, его следует рассматривать как реальный газ, функции которого определяются в зависимости от двух переменных (например, P,t), с учетом коэффициента Джоля-Томпсона, характеризующим отличие реального газа от идеального.
Что такое политропная мощность компрессора
Электронная библиотека
Основная цель термодинамического расчета компрессора – это определение работы (мощности), которую следует затратить, чтобы получить некоторое количество газа при заданных параметрах начала и конца сжатия. Работу определяют по уравнению (9.1).
Когда процесс сжатия идет по изотерме pv = const, работа идеального «изотермического» компрессора, отнесенная к 1 кг газа, с учетом того, что
При адиабатном сжатии работа сжатия равна:
Работу «адиабатного» компрессора находят из выражения:
Пользуясь выражением (9.4), работу компрессора удобно рассчитывать с помощью hS-диаграммы.
Как адиабатный, так и изотермический процессы сжатия газа могут рассматриваться только как теоретические. В действительности процессы сжатия идут по политропе, имеющей переменный показатель. Показатель политропы зависит от интенсивности теплообмена в процессе сжатия газа в компрессоре:
· для охлаждаемого компрессора k > n > 1;
· для неохлаждаемого компрессора (центробежного, осевого) n > k.
Для политропного процесса работа сжатия равна:
Следовательно, работу «политропного» компрессора можно найти по формуле:
Среднее значение показателя политропы, как правило, определяется по параметрам газа в начале и конце процесса сжатия.
В случае охлаждаемого компрессора (рис.
lиз Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Работа и мощность политропического компрессора
Идеальный компрессор, процесс сжатия в котором протекает по политропе, т.е. по закону рV n = const, называется политропическим идеальным компрессором (n — показатель политропы сжатия, 1 3 сжимаемого газа, определяется по формуле

Мощность идеального политропического компрессора определяется формулами

где n – частота вращения вала, об/мин:
Lк.пол. — работа идеального политропического компрессора, определяемая формулой (106).
Влияние термодинамического процесса сжатия на экономичность работы компрессора
Сравнивая величины работ при различных процессах сжатия (это видно на индикаторной диаграмме рис.13), можно убедиться, что наивыгоднейшим процессом сжатия является процесс изотермический. Полная работа, затрачиваемая в цилиндре идеального изотермического компрессора, оказывается из всех работ минимальной.
Таким образом, заштрихованная площадка на рис. 13 численно равна работе, сэкономленной в изотермическом компрессоре по сравнению с работой адиабатического компрессора, в одном цикле. Величина этой экономии, как видим из формулы (106), зависит не только от значения показателя политропы сжатия, но и степени повышения давления газа в цилиндре. При степенях сжатия e = 6 ¸ 8 экономия в работе, как показывают расчеты, может составить от 32 до 38 %.
Температура в конце сжатия и определение предельной степени повышения давления воздуха по температурному фактору
Температура в конце сжатия газа в цилиндре определяется по формулам:
а) для адиабатического идеального компрессора

б) для политропического идеального компрессора

где Т1 и Т2 — абсолютные температуры воздуха в начале и конце сжатия, °К;
e — степень сжатия газа в цилиндре, определяемая формулой 
Внутренняя поверхность цилиндра поршневых компрессоров смазывается маслом, имеющим определенную температуру вспышки. Например, компрессорное масло (Т19) имеет температуру вспышки 241°С.
Согласно требованиям «Правил устройства и безопасной эксплуатации стационарных компрессорных установок, воздухопроводов и газопроводов», температура воздуха после каждой ступени сжатия для компрессоров, используемых в промышленности, не должна быть выше 170°.
Если принять, что в компрессоре происходит адиабатный (самый неблагоприятный по температурному фактору) процесс сжатия, и что в летнее время температура всасываемого (атмосферного) воздуха составляет 25°С, то из формулы (111) получим формулу, определяющую максимально возможную степень сжатия по температурному фактору
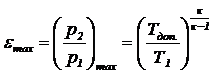
Так как Т2 = Тдоп = 273 + 170 = 433 ° К; Т1 = 273 + 25 = 298 ° К, то расчет по формуле (114) дает результат
Таким образом, степень повышения давления в цилиндре компрессора ограничивается безопасностью работы и конечное давление, если начальное равно 1 ат, не может быть больше 4 ат. В большинстве случаев для нормальной работы машин и механизмов с пневмоприводом необходимо давление сжатого воздуха более 4 ат.
Поэтому в настоящее время используются преимущественно двухступенчатые компрессоры с охлаждением воздуха между ступенями, позволяющие получать конечное давление воздуха до 9 ат. Все сказанное относится к воздушным компрессорам общего назначения.
Дата добавления: 2018-04-15 ; просмотров: 1381 ; Мы поможем в написании вашей работы!
Polytropic Efficiency
Polytropic efficiency is defined by:(5.14)n(n−1)=[k(k−1)]ηpwhere:
Related terms:
Compressor and Turbine Performance Characteristics
Polytropic Efficiency
Polytropic efficiency is another concept of efficiency often used in compressor evaluation. It is often referred as small stage or infinitesimal stage efficiency. It is the true aerodynamic efficiency exclusive of the pressure-ratio effect. The efficiency is the same as if the fluid is incompressible and identical with the hydraulic efficiency:
which can be expanded using a Taylor expansion series and assuming that:
The expansion of the numerator is:
The expansion of the denominator is:
Neglecting second and above order terms, since dPt2/Pt1 ≪ 1, the following relationship is obtained:
From this relationship, it is obvious that polytropic efficiency is the limiting value of the isentropic efficiency as the pressure increase approaches zero, and the value of the polytropic efficiency is higher than the corresponding adiabatic efficiency. Figure 3-12 shows the relationship between adiabatic and polytropic efficiencies as the pressure ratio across the compressor increases. Figure 3-13 shows the relationship across the turbine.
Another characteristic of polytropic efficiency is that the polytropic efficiency of a multistage unit is equal to the stage efficiency if each stage has the same efficiency.
Transportation Systems
11.3.3 Centrifugal Compressors
Although the adiabatic compression process can be assumed in centrifugal compression, polytropic compression process is commonly considered as the basis for comparing centrifugal compressor performance. The process is expressed as
where n denotes the polytropic exponent. The isentropic exponent k applies to the ideal frictionless adiabatic process, while the polytropic exponent n applies to the actual process with heat transfer and friction. The n is related to k through polytropic efficiency Ep:
The polytropic efficiency of centrifugal compressors is nearly proportional to the logarithm of gas flow rate in the range of efficiency between 0.7 and 0.75. The polytropic efficiency chart presented by Rollins (1973) can be represented by the following correlation:
q1 = gas capacity at the inlet condition, cfm.
There is a lower limit of gas flow rate, below which severe gas surge occurs in the compressor. This limit is called “surge limit.” The upper limit of gas flow rate is called “stone-wall limit,” which is controlled by compressor horsepower.
The procedure of preliminary calculations for selection of centrifugal compressors is summarized as follows:
Calculate compression ratio based on the inlet and discharge pressures:
Based on the required gas flow rate under standard condition (q), estimate the gas capacity at inlet condition (q1) by ideal gas law:
Find a value for the polytropic efficiency Ep from the manufacturer’s manual based on q1.
Calculate polytropic ratio (n-1)/n using Eq. (11.67) :
Calculate discharge temperature by
Estimate gas compressibility factor values at inlet and discharge conditions.
Calculate gas capacity at the inlet condition (q1) by real gas law:
Repeat Steps 2–7 until the value of q1 converges within an acceptable deviation.
Calculate gas horsepower by
Some manufacturers present compressor specifications using polytropic head in lbf-ft/lbm defined as
Calculate gas horsepower by:
The proceeding equations have been coded in the spreadsheet CentrifugalCompressorPower.xls for quick calculations.
Size a centrifugal compressor for the following given data:
| Gas-specific gravity: | 0.68 |
| Gas-specific heat ratio: | 1.24 |
| Gas flow rate: | 144 MMscfd at 14.7 psia and 60 °F |
| Inlet pressure: | 250 psia |
| Inlet temperature: | 100 °F |
| Discharge pressure: | 600 psia |
| Polytropic efficiency: | Ep = 0.61 + 0.03 log (q1) |
Solution Calculate compression ratio based on the inlet and discharge pressures:
Calculate gas flow rate in scfm:
Based on the required gas flow rate under standard condition (q), estimate the gas capacity at inlet condition (q1) by ideal gas law:
Find a value for the polytropic efficiency based on q1:
Calculate polytropic ratio (n–1)/n:
Calculate discharge temperature:
Estimate gas compressibility factor values at inlet and discharge conditions (spreadsheet program Hall-Yaborough-z.xls can be used):
Calculate gas capacity at the inlet condition (q1) by real gas law:
Calculate the new polytropic ratio (n–1)/n:
Calculate the new discharge temperature:
Estimate the new gas compressibility factor value:
Because z2 did not change, q1 remains the same value of 7,977 cfm.
Calculate gas apparent molecular weight:
Calculate polytropic head:
Calculate gas horsepower requirement:
Centrifugal compressor efficiency types and rational application
LOSS ESTIMATION
The loss model of the TU SPb Universal modeling method (3,4) is based on summarizing losses in each element of a centrifugal compressor stage. Therefore the programs provide information to present T – S — diagram with n = var in a stage elements. Several “real” T – S — diagrams by Universal modeling method are presented below. Calculation of entropy change by well-known formula S 2 − S 1 = R k − 1 ln p 2 ρ 2 k − ln p 1 ρ 1 k (9) is not applicable for flow path elements where change of pressure and density is too small. The simplified formula based on dS = d h r T was used instead:
The computer programs of Universal modeling method calculate efficiency that we name “real” polytropic efficiency:
A polytropic efficiency that is used in engineering practice and that is measured in plant tests of compressors in accordance with (12) is defined by the next equation:
The “real” efficiency is higher in all cases. It is not important for engineering practice but it must be meant when results of modeling are compared with test data.
Wet Gas Compression
Direct Integration Approach
Characterizing the performance of wet gas compression is difficult when defining a polytropic efficiency using the widely accepted equations from ASME PTC-10. The equations of PTC-10 are based on the method presented by Schultz to characterize compressor polytropic performance using real gases instead of the ideal gas assumption. In the method, the inlet and exit conditions of the compressor are used along with gas properties taken at the average conditions between the inlet and exit. In wet gas compression, however, the compression process is expected to have a significant effect on the fluid properties due to phase change of the liquid. Therefore, a direct integration method has been used to quantify wet gas compression by iterating along incremental pressure steps through the compression process. In this method, the polytropic efficiency is estimated for the calculation and held constant for all iteration steps. From the method, the polytropic head and efficiency for the compressor are determined when the calculated discharge temperature matches the actual value. The direct-integration method has been shown by Huntington to be more accurate than the Schultz method, and is compared among different equations of state by Hundseid. A major advantage of the direct-integration method over the Schultz method is that the fluid properties are calculated for each step in the calculation instead of an average. Therefore, the method is better suited for high-pressure ratio impellers or applications with significant property variation. The direct-integration method has been applied to wet gas compression data by Hundseid to illustrate the large difference between the Schultz and direct-integration methods for wet gas compression. The drawback to the direct-integration method, however, is that both fluid phases are assumed to be in equilibrium. This leads to the fact that the prediction method is based on knowing the discharge temperature of the compressor, which is difficult to establish whether the measured value at the discharge flange is either the liquid or gas temperature. Nevertheless, the direct-integration method provides a promising approach to characterizing wet gas performance.
Gas Compressors
5.2.2 Polytropic calculation
Sometimes, compressor manufacturers use a polytropic path instead of isentropic. Polytropic efficiency is defined by:
n = polytropic exponent or number of moles
η = efficiency, expressed as a decimal
The equations for head and gas horsepower based upon polytropic compression are:
M = molecular mass, kg/kg mol
n = polytropic exponent or number of moles
R = universal gas constant = 8.314 kJ/(kmol·K)
T = absolute temperature, K
Which also can be written in the form:
Polytropic and isentropic head are related by:
The approximate actual discharge temperature can be calculated from:
Centrifugal compressors shall be designed in accordance with American Petroleum Institute (API) Standard No. 617.
The centrifugal (radial flow) compressor is well established for the compression of gases and vapors. It has proven its economy and uniqueness in many applications, particularly where large volumes are handled at medium pressures.
Centrifugal compressors shall conform to API Standard No. 617 for all services handling air or gas, except machines developing less than 35 kPa (0.35 bar) from atmospheric pressure, which may be classified as fans or blowers.
Compressors shall be guaranteed for head, capacity, and satisfactory performance at all specified operating points and further shall be guaranteed for power at the rated point.
The volume capacity at the surge point shall not exceed the specified percentage of normal capacity at normal speed, and normal (unthrottled) suction conditions. The rise in pressure ratio from normal capacity to the surge point at normal speed shall not be less than that specified.
The head developed at 115% of normal capacity at normal speed shall be not less than approximately 85% of the head developed at the normal operating point.
The head capacity characteristic curve shall rise continuously from the rated point to the predicted surge. The compressor, without the use of a bypass, shall be suitable for continuous operation at any capacity at least 10% greater than the predicted approximate surge capacity shown in the proposal.
For variable-speed compressors, the head and capacity shall be guaranteed with the understanding that the power may vary ±4%.
For constant-speed compressors, the specified capacity shall be guaranteed with the understanding that the head shall be within ±5% and −0% of that specified; the power shall not exceed stated power by more than 4%. These tolerances are not additive.
The compressor manufacturer shall be responsible for checking the “k” (ratio of specific heats) and “Z” (compressibility factor) values specified against the gas analysis specified.
Compressor Mach numbers shall not exceed 0.90 when measured at any point.
Gas purification, compression and liquefaction processes and technology for carbon dioxide (CO2) transport
12.4.1 Compression and cooling
The gas and steam turbines and combined cycle in IGCC systems
15.3.12 Polytropic efficiency versus isentropic efficiency for compressors and turbines
The efficiency of a compressor is usually quoted as the isentropic efficiency (ηc) of the entire compressor; often another efficiency, referred to as polytropic efficiency (ηc,p), is also used in turbomachinery to describe the elemental efficiency of a differential piece of a stage. The concept of using the polytropic efficiency lies on the fact that the increase in temperature due to irreversible friction in one stage results in more work being required in the next stage. The effect is termed the preheat effect. The polytropic efficiency—also called “small-stage efficiency”—is defined as the isentropic efficiency of an elemental (or differential) stage in the process such that it is constant throughout the whole process. The relationship between the isentropic and polytropic compressor efficiency is given by Cohen et al. (1999) as:
The difference between ηc,p and ηc increases as compression ratio increases. Isentropic compressor efficiency is usually degraded from the polytropic compressor efficiency (i.e., ηc,p > ηc).
Similar, but opposite, to the polytropic compressor efficiency, the irreversible friction heat of the prior stage is recovered as work in the next stage, resulting in a polytropic turbine efficiency (ηt,p) being lower than the isentropic turbine efficiency (ηt), i.e., ηt,p Cohen et al. (1999) as:
where P4/P3 is the turbine expansion ratio, which is the inverse of the compression pressure ratio (1/PR). The foregoing relations cannot be applied to a steam turbine as vapors generally do not obey the gas law. The reheat factor (RH) is used to measure the hidden inefficiency of the complete expansion (from state 1 to state 2) due to the irreversibility.
where, Δhs,p is the isentropic small-stage enthalpy of an elemental stage of the steam turbine blades and ηST,p is the polytropic steam turbine efficiency. RH is usually between 1.03 and 1.08.
12th International Symposium on Process Systems Engineering and 25th European Symposium on Computer Aided Process Engineering
4 Example
| Stream | Ts, K | Tt, K | mcp, kW/K | ΔH, kW | ps, bar | pt, bar |
|---|---|---|---|---|---|---|
| H1 | 288 | 124 | 4 | 656 | 3 | 1 |
| H2 | 242 | 148 | 9 | 846 | — | — |
| C1 | 120 | 208 | 7 | 616 | — | — |
| C2 | 168 | 284 | 8 | 928 | — | — |
| Heat source | 288 | 288 | — | — | — | — |
| Cooling source | 120 | 120 | — | — | — | — |
| Cases | Ts, K | Tt, K | mcp, kW/K | ΔH, kW | Ps, bar | pt, bar |
|---|---|---|---|---|---|---|
| Case A | ||||||
| H1 | 210.4 | 124 | 4 | 345.6 | 1 | 1 |
| Case B | ||||||
| H1_1 | 288 | 242 | 4 | 184 | 3 | 3 |
| H1_2 | 176.8 | 124 | 4 | 211.2 | 1 | 1 |
| Case C | ||||||
| H1_αl | 288 | 242 | 1.07 | 49.2 | 3 | 3 |
| H1_α2 | 176.8 | 124 | 1.07 | 56.5 | 1 | 1 |
| H1_β | 210.4 | 124 | 2.93 | 253.2 | 1 | 1 |
| Case D | ||||||
| H1_αl | 288 | 242 | 1.07 | 49.2 | 3 | 3 |
| H1_α2 | 176.8 | 124 | 1.07 | 56.5 | 1 | 1 |
| Hl_βl | 288 | 172 | 1.56 | 181.0 | 3 | 3 |
| Hl_β2 | 125.7 | 124 | 1.56 | 2.7 | 1 | 1 |
| Hl_γ | 210.4 | 124 | 1.37 | 118.4 | 1 | 1 |
| Case E | ||||||
| Hl_βl | 288 | 172 | 1.56 | 181.0 | 3 | 3 |
| Hl_β2 | 125.7 | 124 | 1.56 | 2.7 | 1 | 1 |
| H1_γ | 210.4 | 124 | 2.44 | 210.8 | 1 | 1 |






