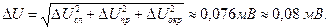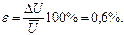Что такое полная погрешность

Научная электронная библиотека

Сибагатуллина А. М., Мазуркин П. М.,

2.6. Обработка результатов измерений

Обработка прямых измерений. Для характеристики большинства приборов часто используют понятие приведенной погрешности, равной абсолютной погрешности в процентах диапазона шкалы измерений. По приведенной погрешности приборы разделяются на классы точности. Класс точности указан на панели прибора.

Наибольшая инструментальная погрешность измеряется по формуле:

, (2.1)

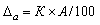
где К – класс точности, А – наибольшее значение шкалы прибора.

Инструментальную погрешность невозможно уменьшить статистической обработкой отсчетов.

При наличии случайных погрешностей наблюдаемые значения измеряемой величины при многократных измерениях случайным образом рассеяны относительно ее истинного значения. В этом случае действительное значение находят как наиболее вероятное из серии отсчетов, а погрешность характеризуют шириной интервала, который с заданной вероятностью показывает истинное значение [44].

Наилучшей оценкой истинного значения величины Х является выборочное среднее значение

, (2.2)

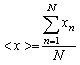
где 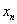– отсчет величины Х, – число отсчетов.

Для оценки разброса отсчетов при измерении используется выборочное среднее квадратическое отклонение отсчетов

. (2.3)

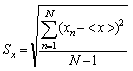
Выборочное среднее является случайной величиной и его разброс относительно истинного значения измеряемой величины оценивается выборочным средним квадратическим отклонением среднего значения

. (2.4)

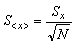
Доверительным интервалом называется интервал 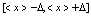, который с заданной степенью достоверности включает в себя истинное значение измеряемой величины.

Доверительной вероятностью (надежностью) результата серии наблюдений называется вероятность 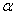, с которой доверительный интервал включает истинное значение измеряемой величины.

Случайную составляющую погрешности принято выражать как полуширину доверительного интервала. Случайная составляющая погрешности многократных измерений

, (2.5)

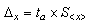
где 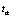– безразмерный коэффициент доверия (коэффициент Стьюдента).

Чем больше доверительная вероятность, тем надежнее оценка интервала и, вместе с тем, шире его границы.

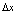
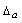
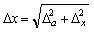
Полная абсолютная погрешность прямых измерений равна квадратической сумме ее составляющих: инструментальной – и случайной –

. (2.6)

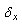
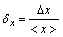
Полная относительная погрешность прямых измерений равна отношению полной абсолютной погрешности к выборочному среднему значению

. (2.7)

Обработка косвенных измерений [44]. Расчет погрешностей косвенных измерений осуществляется по алгоритму, использующему сложение абсолютных величин погрешностей.

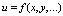
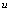
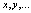
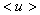
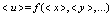
Пусть – функциональная зависимость между измеряемой величиной и величинами , значения которых найдены прямыми измерениями. Действительное значение определяется как:

. (2.8)

Вычисляем относительные погрешности аргументов. Затем определяем абсолютную и относительную погрешности функции

(2.9)

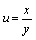
— для относительной погрешности

; (2.10)

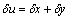
— для абсолютной погрешности

. (2.11)

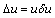
Оценка токсического действия тестируемой пробы воды. Оценка токсического действия тестируемой пробы воды делается на основании достоверности различий между показателями прироста численности клеток водорослей в контроле и в опыте. При этом вычисляют [14]:

– средние арифметические величины прироста численности клеток – X_i и X (в контроле и опыте);

– среднее квадратичное отклонение по формуле 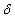(2.3);

– ошибку среднего арифметического (X):

– Td – критерий достоверности различий двух величин:

; (2.12)

, (2.13)

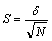
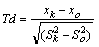
где x_k и x_о – сравниваемые средние величины (в контроле и опыте),

Sk 2 и So 2 – квадраты ошибок средних в контроле и опыте.

Td рассчитывают для каждой тестируемой пробы и сравнивают с табличной величиной Tst – стандартным значением критерия Стьюдента. В нашем случае для его определения принимаем уровень значимости р = 0,05 (95%) и степень свободы = (n1 + n2 – 2), т. е. (3 + 3 – 2) = 4. Tst при степени свободы 4 равно 2,78.

Если Td ≥ Tst, то различие между контролем и опытом достоверно – тестируемая вода загрязнена.

Источник

Погрешность округления. Полная погрешность прямого измерения

Как уже говорилось выше, на измеренное значение физической величины влияют случайные и систематические ошибки, в частности ошибки измерительного прибора. Очевидно, эти факторы необходимо учитывать и при вычислении полной погрешности прямого измерения.

Кроме случайной погрешности и погрешности прибора необходимо учитывать и погрешность округления. Это погрешности связанные дискретностью шкалы или индикации измерительного прибора и необходимостью округления промежуточного значения (между соседними рисками шкалы или значениями цифрового индикатора).

Интервал округления h может быть различным. Если отсчет снимается с точностью до целого деления, то интервал округления равен цене деления шкалы прибора (дискрету младшего знака индикатора). Если отсчет округляется до половины деления, интервал округления равен половине цены деления и т.д. Максимальная погрешность округления, очевидно, не превышает половины интервала округления т.е. величин h/2.

Для доверительной вероятности Р можно записать выражение абсолютной погрешности округления

. (1.14)

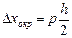
Пример. Пусть значение тока в цепи, измеренное при помощи амперметра равно I. Шкала прибора имеет деление ценой 0,1 мА. Отсчет округляется до одного деления, т.е. до 0,1 мА. Значит, величина h=0,1 мА, а абсолютная погрешность округления

= 0,95 ∙ 0,1 мА/2 ≈ 0,048 мА ≈ 0,05 мА

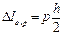
Градуировка измерительных приборов обычно производится так, чтобы деление шкалы было в интервале [δ; 2δ]. Тогда при округлении до половины деления (наиболее удобном) Δx_окр будет вдвое меньше приборной погрешности δ и поэтому ее вклад в полную погрешность несущественен. Отсюда можно вывести весьма полезное правило: если не известна погрешность измерительного прибора, то ее можно оценочно принять равной половине цены деления шкалы. Правило справедливо если прибор не перестраивали после изготовления с помощью дополнительного сопротивления или шунта.

В теории вероятностей показывается, что погрешность, обусловленная несколькими независимыми факторами, определяется квадратичным суммированием. Поскольку в лабораторных учитываются сразу три погрешности, то полная абсолютная погрешность прямого измерения

. (1.15)

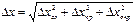
а относительная погрешность

. (1.16)

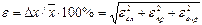
При вычислении всех суммируемых погрешностей доверительная вероятность Р выбирается одинаковой (например, р=0,95). Такой же оно будет и для полной погрешности. Если какая-либо из погрешностей раза в три меньше любой другой, ее вклад в полную погрешность незначителен и ею можно пренебречь.

Рассмотрим на конкретном примере полную обработку результатов прямых измерений.

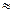
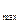
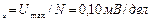
Пример. Пусть измеряется э.д.с. датчика Холла. Контрольное наблюдение показало, что U 12 мВ. Поэтому для измерения выбран предел милливольтметра U =15 мВ. Класс его точности к=0,5. Количество делений на равномерной шкале N=150 делений. Цена деления шкалы прибора С .

Первые три измерения показали, что в опыте появляется разброс данных, обусловленный случайными ошибками. Поэтому количество наблюдений увеличено до десяти. Полученные результаты приведены в таблице 1.3.

Номер наблюдения	U	ΔU	Номер наблюдения	U	ΔU
мВ	мВ	мВ	мВ
12,05	-0,065	12,10	-0,015
12,20	+0,085	12,00	-0,115
12,10	-0,015	12,15	+0,035
12,05	-0,065	12,10	-0,015
12,15	+0,035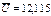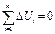
12,25	+0,135

1. Рассчитать среднее арифметическое 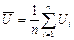=12,115 мВ.

2. Определить случайные отклонения .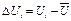

3. Проверить равенство нулю алгебраической суммы всех значений ΔU.

4. Рассчитать случайную погрешность (при Р=0,95).

мВ=0,053 мВ

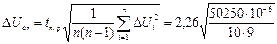
5. Определить приборную погрешность измерения.

мВ.

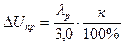
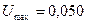
6. Найти погрешность округления (интервал округления h=0,05 мВ).

=0,024 мВ.

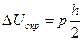
7. Определить полную погрешность измерения.

8. Вычислить относительную погрешность измерения.

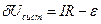
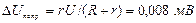
9. Найти поправку на систематическую погрешность метода: вольтметр измеряет не ЭДС, а напряжение. Поэтому необходимо учитывать падение напряжения на нем самом. С учетом закона Ома систематическая ошибка . Тогда систематическая поправка определяется из выражения.

.

Поправка на порядок меньше полной погрешности, поэтому ею можно пренебречь.

10. Записать окончательный результат

U=12,12+0,08 мВ; ε=0,6% ; р=0,95.

В заключение этого раздела несколько слов о количестве повторных наблюдений. Как следует из (1.10), большое количество наблюдений позволит уменьшать случайную погрешность. Однако, это требует дополнительных затрат времени, труда, энергии и т.д. Поэтому вопрос о количестве наблюдений должен быть обдуман и обоснован (особенно в случае сложных и затратных экспериментов). По возможности следует стремиться к тому, чтобы случайная погрешность стала меньше приборной или по крайней мере сравнялась с ней. Нельзя ограничиваться одним наблюдением, оно может содержать промах и по его результату невозможно определить погрешность. Несколько (3…5) повторных наблюдений это тот минимум на основании которого можно оценить ситуацию. Если результаты совпали, то случайные ошибки меньше приборной и на этом количестве наблюдений можно ограничиться. Если в результатах обнаружится разброс, то проводят серию повторных наблюдений, добиваясь уменьшения случайной погрешности.

Таким образом, вопрос о количестве повторных наблюдений решается в ходе эксперимента. На основании анализа полученных результатов, сравнения случайной и приборной погрешностей, учета требований предъявляемых к точности окончательного результата.

Источник

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

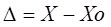
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

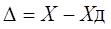
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

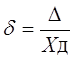
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

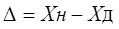
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

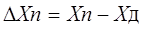
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

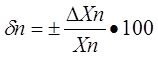
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

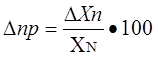
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник