Что такое полное давление
Полное давление
Смотреть что такое «Полное давление» в других словарях:
полное давление — (po) Давление изоэнтропически заторможенного газа. [ГОСТ 23281 78] Тематики аэродинамика летательных аппаратов Обобщающие термины характеристики течения газа EN total pressure … Справочник технического переводчика
Полное давление (pv, Па) — Разность полных давлений воздушного потока при выходе и перед входом в вентилятор, включающий диффузор и элементы подсоединения к шахтной сети (коллектор, входную коробку) Источник: ГОСТ 11004 84: Вентиляторы шахтные главного проветривания.… … Словарь-справочник терминов нормативно-технической документации
полное давление — visuminis slėgis statusas T sritis fizika atitikmenys: angl. total pressure vok. Gesamtüberdruck, m; Gesamtdruck, m rus. полное давление, n; суммарное давление, n pranc. pression totale, f … Fizikos terminų žodynas
полное давление — visuminis slėgis statusas T sritis Energetika apibrėžtis Dinaminio ir statinio slėgių suma. atitikmenys: angl. total pressure vok. Gesamtdruck, m rus. полное давление, n; суммарное давление, n pranc. pression totale, f … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
полное давление — visuminis slėgis statusas T sritis Standartizacija ir metrologija apibrėžtis Manometrinio ir dinaminio slėgių suma. atitikmenys: angl. total pressure vok. Gesamtüberdruck, m; Gesamtdruck, m rus. полное давление, n pranc. pression totale, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полное давление — Давление в рассматриваемой точке потока газа при предположении адиабатного торможения газа в этой точке до нулевой скорости … Политехнический терминологический толковый словарь
полное давление — потока, давление торможения, давление p0 изоэнтропически заторможенной жидкости или газа. Физически П. д. характеризует собой ту часть энергии потока, которая участвует в обратимых процессах перехода между кинетической энергией и давлением … Энциклопедия «Авиация»
полное давление — потока, давление торможения, давление p0 изоэнтропически заторможенной жидкости или газа. Физически П. д. характеризует собой ту часть энергии потока, которая участвует в обратимых процессах перехода между кинетической энергией и давлением … Энциклопедия «Авиация»
ПОЛНОЕ ДАВЛЕНИЕ — потока, давление торможения, давление изоэнтропически заторможенной жидкости или газа (см. Изоэнтропийный процесс), физически П. д. характеризует собой ту часть энергии потока, к рая участвует в обратимых процессах перехода между кинетич.… … Большой энциклопедический политехнический словарь
полное давление
ρgz + 
где ρ плотность, р давление, V модуль вектора скорости. Если постоянная Бернулли С одна и та же для всего потока, то П. д. постоянно в плоскости z = const, но различно по значению для разных плоскостей. В аэродинамике массовыми силами обычно пренебрегают, поэтому уравнение принимает вид

Следовательно, П. д. постоянно вдоль линии тока, но в общем случае изменяется при переходе от одной линии тока к другой. Если набегающий на тело поток однороден, то П. д. одно и то же для всего течения.
Для установившегося изоэнтропического течения совершенного газа (то есть для сжимаемой среды) в элементарной трубке тока П. д. связано с газодинамическими переменными потока уравнением Бернулли, которое в этом случае при отсутствии массовых сил может быть записано в виде

где γ показатель адиабаты, М местное Маха число. Если рассматриваемая линия тока пересекает ударную волну, то при прохождении через неё П. д. уменьшается и принимает новое значение, которое остаётся неизменным вдоль линии тока, пока она вновь не пересечёт ударную волну. Это изменение П. д. в ударных волнах и других диссипативных процессах характеризуется коэффициентом восстановления полного давления.
Понятие «П. д.» используется при проведении различных газодинамических расчётов и
при анализе экспериментальных данных. Так, например, распределение значений p0 и p в потоке может быть сравнительно просто измерено, а на основе этих данных можно провести определение локальных значений газодинамических переменных по двум последним формулам для изоэнтропического потока или по иным модифицированным формулам, учитывающим потери П. д. в ударных волнах.
Полезное
Смотреть что такое «полное давление» в других словарях:
Полное давление — потока, давление торможения, давление p0 изоэнтропически заторможенной жидкости или газа. Физически П. д. характеризует собой ту часть энергии потока, которая участвует в обратимых процессах перехода между кинетической энергией и давлением. Эта… … Энциклопедия техники
полное давление — (po) Давление изоэнтропически заторможенного газа. [ГОСТ 23281 78] Тематики аэродинамика летательных аппаратов Обобщающие термины характеристики течения газа EN total pressure … Справочник технического переводчика
Полное давление (pv, Па) — Разность полных давлений воздушного потока при выходе и перед входом в вентилятор, включающий диффузор и элементы подсоединения к шахтной сети (коллектор, входную коробку) Источник: ГОСТ 11004 84: Вентиляторы шахтные главного проветривания.… … Словарь-справочник терминов нормативно-технической документации
полное давление — visuminis slėgis statusas T sritis fizika atitikmenys: angl. total pressure vok. Gesamtüberdruck, m; Gesamtdruck, m rus. полное давление, n; суммарное давление, n pranc. pression totale, f … Fizikos terminų žodynas
полное давление — visuminis slėgis statusas T sritis Energetika apibrėžtis Dinaminio ir statinio slėgių suma. atitikmenys: angl. total pressure vok. Gesamtdruck, m rus. полное давление, n; суммарное давление, n pranc. pression totale, f … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
полное давление — visuminis slėgis statusas T sritis Standartizacija ir metrologija apibrėžtis Manometrinio ir dinaminio slėgių suma. atitikmenys: angl. total pressure vok. Gesamtüberdruck, m; Gesamtdruck, m rus. полное давление, n pranc. pression totale, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полное давление — Давление в рассматриваемой точке потока газа при предположении адиабатного торможения газа в этой точке до нулевой скорости … Политехнический терминологический толковый словарь
полное давление — потока, давление торможения, давление p0 изоэнтропически заторможенной жидкости или газа. Физически П. д. характеризует собой ту часть энергии потока, которая участвует в обратимых процессах перехода между кинетической энергией и давлением … Энциклопедия «Авиация»
ПОЛНОЕ ДАВЛЕНИЕ — потока, давление торможения, давление изоэнтропически заторможенной жидкости или газа (см. Изоэнтропийный процесс), физически П. д. характеризует собой ту часть энергии потока, к рая участвует в обратимых процессах перехода между кинетич.… … Большой энциклопедический политехнический словарь
ПОЛНОЕ ДАВЛЕНИЕ
По́лное давле́ние потока, давление торможения, давление p0 изоэнтропически заторможенной жидкости или газа. Физически П. д. характеризует собой ту часть энергии потока, которая участвует в обратимых процессах перехода между кинетической энергией и давлением. Эта величина играет важную роль в аэро- и гидродинамике, в особенности при исследовании установившихся адиабатических течений идеальной жидкости. Для стационарного течения идеальной несжимаемой жидкости с потенциалом массовых сил П = gz вдоль линии тока справедливо Бернулли уравнение:
где ρ плотность, р давление, V модуль вектора скорости. Если постоянная Бернулли С одна и та же для всего потока, то П. д. постоянно в плоскости z = const, но различно по значению для разных плоскостей. В аэродинамике массовыми силами обычно пренебрегают, поэтому уравнение принимает вид
Следовательно, П. д. постоянно вдоль линии тока, но в общем случае изменяется при переходе от одной линии тока к другой. Если набегающий на тело поток однороден, то П. д. одно и то же для всего течения.
Для установившегося изоэнтропического течения совершенного газа (то есть для сжимаемой среды) в элементарной трубке тока П. д. связано с газодинамическими переменными потока уравнением Бернулли, которое в этом случае при отсутствии массовых сил может быть записано в виде
где γ показатель адиабаты, М местное Маха число. Если рассматриваемая линия тока пересекает ударную волну, то при прохождении через неё П. д. уменьшается и принимает новое значение, которое остаётся неизменным вдоль линии тока, пока она вновь не пересечёт ударную волну. Это изменение П. д. в ударных волнах и других диссипативных процессах характеризуется коэффициентом восстановления полного давления.
Понятие «П. д.» используется при проведении различных газодинамических расчётов и
при анализе экспериментальных данных. Так, например, распределение значений p0 и p в потоке может быть сравнительно просто измерено, а на основе этих данных можно провести определение локальных значений газодинамических переменных по двум последним формулам для изоэнтропического потока или по иным модифицированным формулам, учитывающим потери П. д. в ударных волнах.
полное давление
ρgz + 
где ρ плотность, р давление, V модуль вектора скорости. Если постоянная Бернулли С одна и та же для всего потока, то П. д. постоянно в плоскости z = const, но различно по значению для разных плоскостей. В аэродинамике массовыми силами обычно пренебрегают, поэтому уравнение принимает вид

Следовательно, П. д. постоянно вдоль линии тока, но в общем случае изменяется при переходе от одной линии тока к другой. Если набегающий на тело поток однороден, то П. д. одно и то же для всего течения.
Для установившегося изоэнтропического течения совершенного газа (то есть для сжимаемой среды) в элементарной трубке тока П. д. связано с газодинамическими переменными потока уравнением Бернулли, которое в этом случае при отсутствии массовых сил может быть записано в виде

где γ показатель адиабаты, М местное Маха число. Если рассматриваемая линия тока пересекает ударную волну, то при прохождении через неё П. д. уменьшается и принимает новое значение, которое остаётся неизменным вдоль линии тока, пока она вновь не пересечёт ударную волну. Это изменение П. д. в ударных волнах и других диссипативных процессах характеризуется коэффициентом восстановления полного давления.
Понятие «П. д.» используется при проведении различных газодинамических расчётов и
при анализе экспериментальных данных. Так, например, распределение значений p0 и p в потоке может быть сравнительно просто измерено, а на основе этих данных можно провести определение локальных значений газодинамических переменных по двум последним формулам для изоэнтропического потока или по иным модифицированным формулам, учитывающим потери П. д. в ударных волнах.
Полезное
Смотреть что такое «полное давление» в других словарях:
Полное давление — потока, давление торможения, давление p0 изоэнтропически заторможенной жидкости или газа. Физически П. д. характеризует собой ту часть энергии потока, которая участвует в обратимых процессах перехода между кинетической энергией и давлением. Эта… … Энциклопедия техники
полное давление — (po) Давление изоэнтропически заторможенного газа. [ГОСТ 23281 78] Тематики аэродинамика летательных аппаратов Обобщающие термины характеристики течения газа EN total pressure … Справочник технического переводчика
Полное давление (pv, Па) — Разность полных давлений воздушного потока при выходе и перед входом в вентилятор, включающий диффузор и элементы подсоединения к шахтной сети (коллектор, входную коробку) Источник: ГОСТ 11004 84: Вентиляторы шахтные главного проветривания.… … Словарь-справочник терминов нормативно-технической документации
полное давление — visuminis slėgis statusas T sritis fizika atitikmenys: angl. total pressure vok. Gesamtüberdruck, m; Gesamtdruck, m rus. полное давление, n; суммарное давление, n pranc. pression totale, f … Fizikos terminų žodynas
полное давление — visuminis slėgis statusas T sritis Energetika apibrėžtis Dinaminio ir statinio slėgių suma. atitikmenys: angl. total pressure vok. Gesamtdruck, m rus. полное давление, n; суммарное давление, n pranc. pression totale, f … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
полное давление — visuminis slėgis statusas T sritis Standartizacija ir metrologija apibrėžtis Manometrinio ir dinaminio slėgių suma. atitikmenys: angl. total pressure vok. Gesamtüberdruck, m; Gesamtdruck, m rus. полное давление, n pranc. pression totale, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полное давление — Давление в рассматриваемой точке потока газа при предположении адиабатного торможения газа в этой точке до нулевой скорости … Политехнический терминологический толковый словарь
полное давление — потока, давление торможения, давление p0 изоэнтропически заторможенной жидкости или газа. Физически П. д. характеризует собой ту часть энергии потока, которая участвует в обратимых процессах перехода между кинетической энергией и давлением … Энциклопедия «Авиация»
ПОЛНОЕ ДАВЛЕНИЕ — потока, давление торможения, давление изоэнтропически заторможенной жидкости или газа (см. Изоэнтропийный процесс), физически П. д. характеризует собой ту часть энергии потока, к рая участвует в обратимых процессах перехода между кинетич.… … Большой энциклопедический политехнический словарь
Уравнение Бернулли — важный закон гидродинамики
Уравнение Бернулли — основной закон гидродинамики. Он имеет физический смысл и практическое применение. Принцип удобно рассмотреть на рисунке.
Что такое уравнение Бернулли
Даниил Бернулли (1700-1782) — физик и математик из Швейцарии, также он изучал медицину, основал математическую физику, гидродинамику. Его известное уравнение отображает зависимость между характеристиками плавно меняющегося жидкого потока, выступает ключевым законом гидродинамики.
Формулируется правило так: полная удельная энергия для струйки идеальной жидкости (ее составляют в сумме удельная энергия положения и давления с кинетической удельной энергией) является неизменной величиной в любых взятых сечениях струйки. Иными словами, в каждой отдельно взятой точке трубопровода энергия потока равняется сумме динамического, весового и статического давлений.
Полная энергия = V + Z + P = константа
Данный принцип является демонстрацией сохранения энергии, одной из наиболее ранних, что стали известны человечеству. Полное давление всегда является постоянным, если только система не пополняется новой энергией (либо часть энергии исчезает).
В законе Бернулли динамическое и весовое давление, соответственно, рассчитываются по своим формулам:
• V =1/2ρv2 (давление динамическое), здесь ρ обозначает плотность жидкости, v —это скорость потока;
• Z =ρgz (давление весовое), здесь ρ — плотность, g — ускорение свободного падения, z обозначает высоту.
P в формуле обозначает давление.
Если рассматривать физическое значение принципа Бернулли, то оно отображает закон сохранения механической энергии по отношению к жидкости, в данном случае идеальной, несжимаемой.
Закон Бернулли в действии
Закон Бернулли следует рассмотреть в действии. Это удобно сделать посредством рисунка.
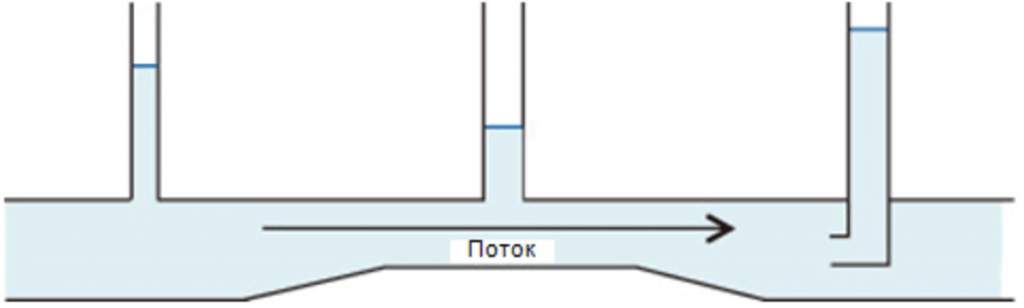
В горизонтальном трубопроводе изображен поток жидкости, она протекает слева направо, не теряя энергию на трение. При этом правая и левая части имеют одинаковый диаметр, а часть, расположенная по центру, имеет диаметр, равный 2/3 от него. Вертикальные (они еще называются пьезометрическими) трубки в центральной и левой областях имеют выход в атмосферу. При этом уровень жидкости в них прямо пропорционален Р (то есть статическому давлению в указанных областях).
Отметим, что давление в области, имеющий больший диаметр, будет превышать этот показатель в узкой области. Это ожидаемо, поскольку скорость в центральном сегменте будет выше. Поэтому согласно принципу швейцарского физика давление снижается вместе с ростом скорости.
Однако статическое давление ведет себя не совсем обычно (оно демонстрируется уровнем жидкости в правой вертикальной трубке). Следует предположить, что оно возвратится к уровню, подобно уровню левой трубки (здесь как условие отсутствуют потери энергии, связанные с трением). Между тем уровень в правой трубке указывает на более высокое давление, в то же время в системе не появляется новая энергия. Дело в том, что столбик с правой стороны является трубкой Пито. Данное приспособление отображает давление особым методом: помимо статического давления, учитывает дополнительное, которое порождается скоростью жидкого потока.
При условии, что если бы с выходящей стороны водного потока оказался закрытым клапан, поток исчезнет. В результате вертикальные трубки демонстрировали бы аналогичное статическое давление вне зависимости от своего положения, а также формы. А после того как поток возобновится, статическое давление (его измеряют пьезометрические трубки) станет равно давлению на конкретном участке. Но у трубки Пито входящее отверстие направляется навстречу потоку (поскольку она имеет внизу изгиб под прямым углом), и он заталкивает туда больше жидкости. Когда вода не течет в трубку (то есть застаивается), то уровень жидкости в ней достигает максимума, равен суммарному динамическому и статическому давлению. Таким образом, давление, фиксируемое трубкой, есть полное давление.
Графическое отображение закона Бернулли
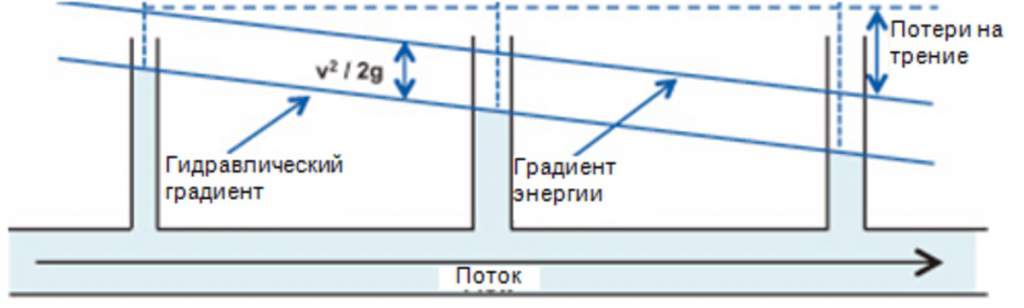
Следующий рисунок представляет уравнение графически. Закон демонстрирует, как ведет себя гидравлическая система, когда изменяются размеры трубы, показатели давления, высоты при потерях энергии на клапанах, соединительных элементах. Данный пример показывает давление в трех разных точках трубопровода при непрекращающемся равномерном потоке неизменной высоты.
Здесь уровень жидкой среды в трубках указывает в обозначенных точках на статическое давление. Линия, что соединяет трубки, носит название гидравлического градиента (то есть пьезометрической линии). Другая наклонная же линия расположена выше, параллельно гидравлическому градиенту и является градиентом энергии, он обозначает полное давление. Измерить его легко посредством трубки Пито или высчитать, зная скоростное значение потока и соответствующую формулу 1/2ρv2.
Градиент энергии есть суммарное статическое давление и скоростной напор в любой взятой точке. На данном рисунке скоростной напор постоянен, а вот гидростатический набор в связи с трением снижается.
Применение закона Бернулли на практике
Указанный закон широко применяется в технике. Так, функционирование многих приборов основано на этом важнейшем правиле гидравлики. Целый ряд устройств разработан на основании принципа Бернулли: например, это карбюратор, эжектор, водоструйный насос, трубчатый расходомер Вентури, сопло, водомерная шайба.
Карбюратор нужен для создания рабочей смеси горючего (подсоса бензина, его смешивания с воздухом) в двигателях внутреннего сгорания. Струйные насосы также очень востребованы в технике, например, в реактивных жидкостных двигателях. Расходомер Вентури необходим в промышленных и лабораторных условиях.
Закон Бернулли применим к полету самолета либо искривленной траектории вращающегося мяча. Он относится и к суднам в море: им нельзя проходить чересчур близко друг к другу, поскольку повышение между ними скорости потока создаст область низкого давления, а это чревато бортовым столкновением. Еще один пример действия уравнения на практике — занавеску в ванной притягивает вода, текущая из душа.