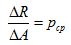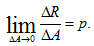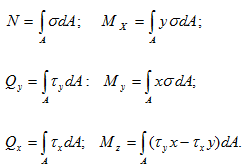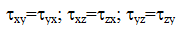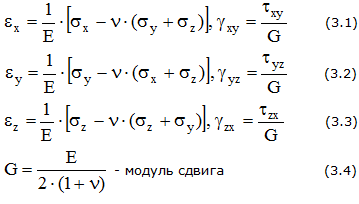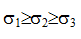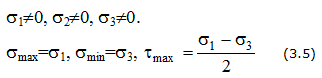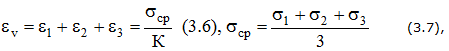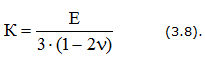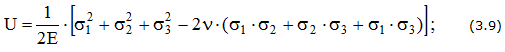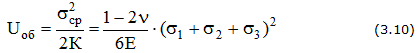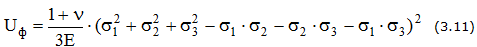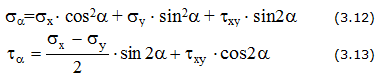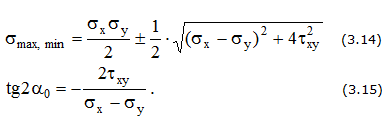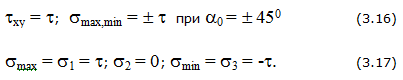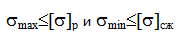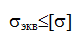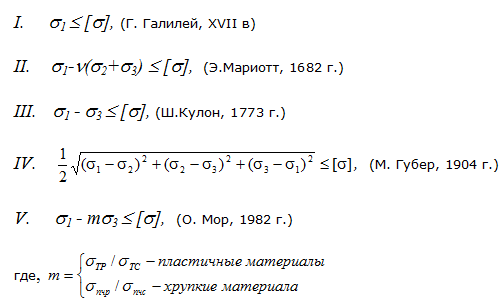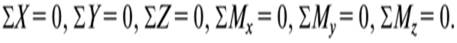Что такое полное напряжение в сопромате

изучаем сопротивление материалов

Напряжения

Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_, \tau_[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

Тензор напряжений

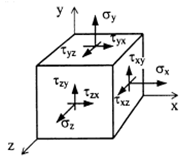
Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений

$$ T _\sigma = \left[\matrix <
\sigma _x & \tau _ & \tau _ \\
\tau _ & \sigma _y & \tau _ \\ \tau _ & \tau _ & \sigma _z
>\right]$$

Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.

При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

В каждой точке можно провести три взаимно-перпендикулярных главных площадки.

При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).

Связь внутренних усилий и напряжений

Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.

Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:

Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.

1 Проекция вектора полного напряжения на нормаль к данной площадке называется нормальным напряжением и обознача­ется через σ_n.

Источник

iSopromat.ru

Рассмотрим понятие о напряженном состоянии в точке и гипотезы прочности. Связь между напряжениями и внутренними силами. Объемное, плоское и линейное напряженное состояния.

Понятие о напряжениях в точке

На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.

Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение

представляет собой среднее напряжение на данной площадке.

Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке

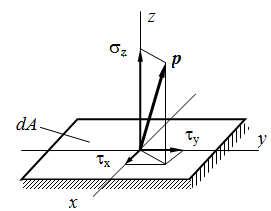
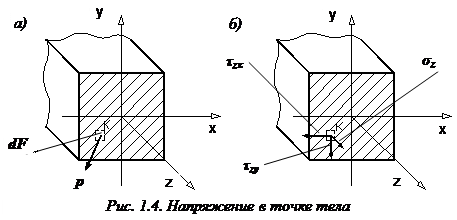
Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.

Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.

Связь между напряжениями и внутренними силами

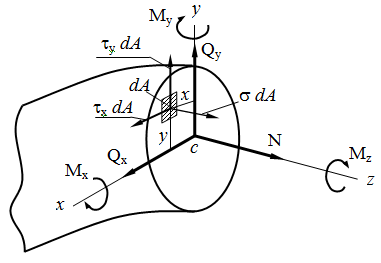
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τ_x dA, τ_y dA.

Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.

Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.

Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.

Объемное напряженное состояние

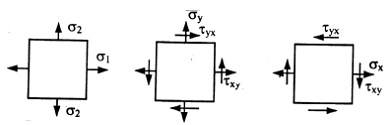
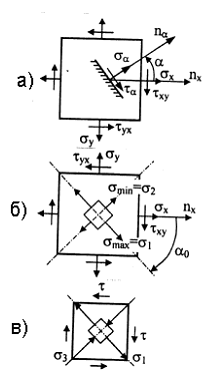
Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).

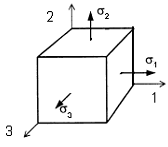
Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:

Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).

Обозначение главных напряжений:

Напряженное состояние называется объемным или трехосным, если

Относительное изменение объема:

где К – модуль объемной упругости,

Удельная потенциальная энергия упругой деформации:

Плоское напряженное состояние

Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).

Напряжения на наклонной площадке (рис. 3.4,а)

Величина и направление главных напряжений (рис. 3.4,б)

Линейное напряженное состояние

Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.

Проверка прочности при линейном напряженном состоянии проводится по условию прочности:

В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:

Величина σ_экв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.

Гипотезы прочности

Существует 5 гипотез прочности:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Напряжение в механике — это мера интенсивности распределения внутренних сил R в окрестности точки в пределах данного сечения площадью A.

Таким образом, напряжения p измеряются в единицах силы, отнесенной к единице площади dA
Полные напряжения в точке
Единица измерения напряжений — Паскаль (Н/м 2 =Па).
Рассмотрим подробнее:

Система приложенных к телу внешних нагрузок, приводит к возникновению в его сечениях внутренней силы R и момента M

Внутренние сила и момент в сечении бруса

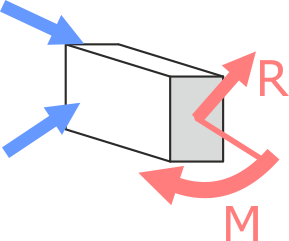
При этом надо понимать что внутренняя сила и внутренний момент воздействуют на всё сечение бруса в целом.

Выделим в рассматриваемом сечении элементарную площадку dA бесконечно малой площади.

Элементарная площадка в сечении бруса

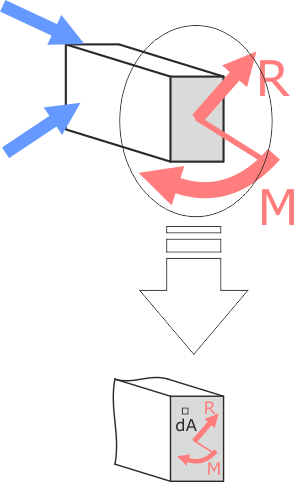
Полное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.

Вектор полного напряжения в точке

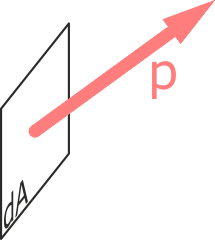
Обозначение полного напряжения в точке – p.
Единица измерения – Паскаль [Па] (Н/м 2 ).

Ввиду того, что большинство конструкционных материалов обладает высокой прочностью часто напряжения, возникающие в них, измеряются в кратных величинах, например мегапаскаль [МПа].

В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):

Нормальное и касательное напряжения

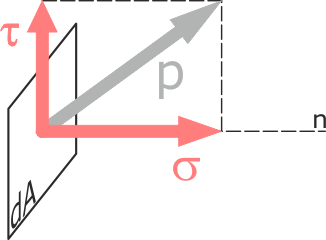
Проекция вектора полного напряжения p на нормаль к сечению называется нормальным напряжением и обозначается через σ, а проекция вектора полного напряжения на плоскость сечения называется касательным напряжением и обозначается через τ.

Разложение вектора полного напряжения на две указанные составляющие имеет конкретный физический смысл – с нормальным напряжением связано разрушение путем отрыва, а с касательным – разрушение путем сдвига или среза.

В частных случаях (например при растяжении-сжатии и кручении) в поперечных сечениях бруса имеют место только нормальные и только касательные напряжения соответственно.

При решении таких задач, величина нормальных и касательных напряжений сравнивается с соответствующими допустимыми значениями напряжений.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Метод сечений. Напряжения полное, нормальное, касательное

Для расчетов деталей и узлов машин на прочность необходимо знать внутренние силы упругости, возникающие в результате действия приложенных к деталям внешних сил.

Метод сечений широко применяется в сопротивлении материалов для определения внутренних сил, поэтому необходимо рассмотреть его подробно. Всякое тело, в том числе деталь или узел машины, можно представлять как систему материальных точек.

В сопротивлении материалов рассматриваются изменяемые (деформируемые) системы материальных точек.

Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается, а взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.

Согласно 3-ему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Рассматривая равновесие любой из двух частей рассеченного тела, получаем одно и то же значение внутренних сил, но лучше рассматривать ту часть тела, для которой уравнения равновесия проще.

Согласно допущению о непрерывности материала тела, можно утверждать, что внутренние силы, возникающие в теле, представляют собой силы, равномерно или неравномерно распределенные по сечению.

Применяя к оставленной части тела условия равновесия, можно найти закон распределения внутренних сил по сечению, а также определить статические эквиваленты этих сил.

Основным расчетным объектом в сопротивлении материалов является брус, и нас интересуют внутренние силы в его поперечном сечении, для чего рассмотрим внутренние силы в поперечном сечении бруса.

Рассечем брус (рис. 1.) поперечным сечением а — а и рассмотрим равновесие его левой части.

Рис. 1.Равновесие левой части бруса.

Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а — а, будут главный вектор F_m, приложенный в центре тяжести сечения, и главный момент М_ТЛ — М_И, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.

Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси, то есть лежащую в плоскости поперечного сечения. Эти составляющие главного вектора вместе с главным моментом назовем внутренними силовыми факторами, действующими в сечении бруса. Составляющую N называют продольной силой, составляющую Q — поперечной силой, а пару сил с моментом М_к — изгибающим моментом.

Для определения указанных трех внутренних силовых факторов статика дает три уравнения равновесия оставленной части бруса, а именно:

(ось z всегда направляем по оси бруса).

Если внешние силы, действующие на брус, не лежат в одной плоскости, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 2), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно:

Рис. 2. 6 внутренних силовых факторов в сечении бруса.

Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия: N — продольная сила, Q_x, Q_y— поперечные силы, М_к — крутящий момент, М_ш, М_иу— изгибающие моменты.

При разных деформациях в поперечном сечении бруса возникают различные внутренние силовые факторы. Рассмотрим частные случаи.

1. В сечении возникает только продольная сила N. В таком случае это деформация растяжения (если сила N направлена от сечения) или деформация сжатия (если сила N направлена к сечению).

2. В сечении возникает только поперечная силаQ. В таком случае это деформация сдвига.

3. В сечении возникает только крутящий моментМ_к. В таком случае это деформация кручения.

4. В сечении возникает только изгибающий моментМ_н. В таком случае это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент М_н и поперечная сила Q, то изгиб называют поперечным.

5. В сечении одновременно возникает несколько внутренних силовых факторов(например, изгибающий и крутящий моменты или изгибаюший момент и продольная сила). В этих случаях имеет место сочетание основных деформаций.

Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение. Напряжение характеризует интенсивность внутренних сил, действующих в сечении.

Рис. 3.Определение напряжения р по методу сечений.

Таким образом, напряжение есть внутренняя сила, отнесенная к единице площади сечения.Напряжение есть величина векторная. Единица напряжения:

Разложим вектор напряжения р на две составляющие: Ϭ — перпендикулярную плоскости сечения и τ— лежащую в плоскости сечения (рис. 1.5). Эти составляющие назовем соответственно нормальным (Ϭ ) и касательным (τ ) напряжением.

Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряжения р определится по формуле

Разложение полного напряжения на нормальное и касательное имеет физический смысл. В поперечном сечении бруса при растяжении, сжатии и чистом изгибе действуют только нормальные напряжения, а при сдвиге и кручении — только касательные напряжения.

Рассмотрим гипотезу, которая носит название принцип независимости действия сил и формулируется так: при действии на тело нескольких нагрузок внутренние силы, напряжения, перемещения и деформации в любом месте могут быть определены как сумма этих величин, найденных от каждой нагрузки в отдельности.

Используя принцип независимости действия сил и начав с изучения простейших основных деформаций, когда в поперечных сечениях бруса действуют только нормальные или только касательные напряжения, в дальнейшем перейдем к изучению сложных деформаций, когда в поперечном сечении действуют и те, и другие напряжения, и рассмотрим случаи сочетания деформаций, которые называют сложным сопротивлением.

Хочу отметить, что принцип независимости действия сил применим только для деталей и узлов, деформации которых малы по сравнению с размерами и пропорциональны действующим нагрузкам.

Вопросы для контрольного оценивания

1. В чем заключается метод сечений

2. Какие три внутренних силовых факторы действуют в поперечном сечении бруса?

3. Какой параметр характеризует напряжение?

4. В каких единицах измеряют напряжение?

5. На какие составляющие раскладывают вектор напряжения?

6. Какие напряжения действуют при растяжении, сжатии и чистом изгибе?

7. Сформулируйте принцип независимости действия сил.

Источник

Напряжение в точке тела

Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения.

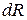
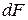
Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы , возникающей на бесконечно малой площадке в окрестности данной точки (рис. 1.4, а).

В количественном выражении .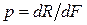

Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K.

Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).

Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.

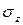
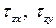
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения ( – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.

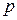
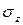
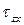
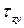
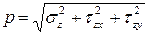
Между полным (), нормальным () и касательными напряжениями ( и ) существует зависимость:

.

Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.

Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:

1 МПа = 106 Па; 1 кН/см2 = 107 Па.

Источник