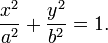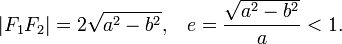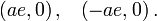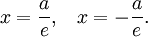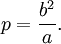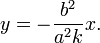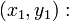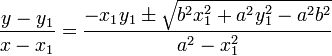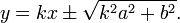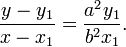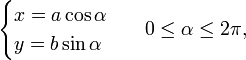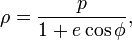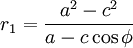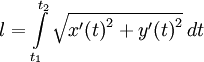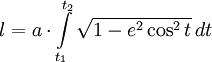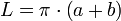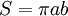Что такое полуось в геометрии
Малая полуось
Э́ллипс (др.-греч. ἔλλειψις — недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1 и F2 (называемых фокусами) постоянна, то есть
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
Содержание
Связанные определения
Свойства
Эллипс также можно описать как
Соотношения между элементами эллипса
Координатное представление
Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Для определённости положим, что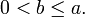 
В этом случае величины a ‘ и b — соответственно, большая и малая полуоси эллипса.
Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:
Координаты фокусов эллипса:
Эллипс имеет две директриссы, уравнения которых можно записать как
Фокальный параметр (т.е. половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен
Уравнение диаметра, сопряжённого хордам с угловым коэффициентом k:
Уравнение касательных, проходящих через точку 
Уравнение касательных, имеющих данный угловой коэффициент k: :
Уравнение нормали в точке
Параметрическое уравнение
Каноническое уравнение эллипса может быть параметризовано:
где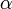 
— параметр уравнения.
Уравнение в полярных координатах
Если принять фокус эллипса за полюс, а ось — за полярную ось, то его уравнение в полярных координатах 
будет иметь вид
где e — эксцентриситет, а p — фокальный параметр.
Пусть r1 и r2 расстояния до данной точки эллипса из первого и второго фокусов. Пусть, также полюс системы координат находится в первом фокусе, а угол φ отсчитывается от направления на второй полюс. Тогда, из определения эллипса,
.
.
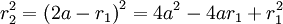
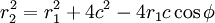
Исключая r2 из последних двух уравнений, получаем
получаем искомое уравнение.
Другое уравнение в полярных координатах:
Длина дуги эллипса
Длина дуги плоской линии определяется по формуле:
Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:
Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллипическому интегралу второго рода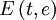 
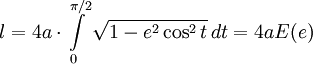
. В частности, периметр эллипса равен:
,
где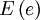 
— полный эллиптический интеграл второго рода.
Приближённые формулы для периметра
YNOT: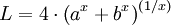 
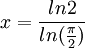
где 
Максимальная погрешность этой формулы
0.3619 % при эксцентриситете эллипса
0.979811 (соотношение осей
1/5). Погрешность всегда положительная.
Очень приближенная формула 
Площадь эллипса
Площадь эллипса вычисляется по формуле
где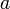 
и 
полуоси эллипса.
Построение эллипса
Пусть даны две взаимноперпендикулярные прямые (оси будущего эллипса) и два отрезка длиной a (большая полуось) и b (малая полуось). Точку пересечения прямых обозначим как O, это центр эллипса.
C помощью циркуля
C помощью циркуля и линейки
Ссылки
См. также
| Конические сечения | |
|---|---|
| Главные типы | Эллипс • Гипербола • Парабола |
| Вырожденные | Точка • Прямая • Пара прямых |
| Частный случай эллипса | Окружность |
| Геометрическое построение | Коническое сечение • Шары Данделена |
| Математика • Геометрия | |
Полезное
Смотреть что такое «Малая полуось» в других словарях:
малая полуось b — 3.22 малая полуось b: Полярная ось эллипсоида. Примечание Для эллипсоида, представляющего Землю, это расстояние от его центра до любого из полюсов. Источник: ГОСТ Р 52572 2006: Географические информационные системы. Координатная основа. Общие… … Словарь-справочник терминов нормативно-технической документации
Малая — незначительное воздействие жидкости на пол, при котором поверхность покрытия пола сухая или слегка влажная; покрытие пола жидкостями не пропитывается. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зд … Словарь-справочник терминов нормативно-технической документации
Большая полуось — это один из основных геометрических параметров объектов, образованных посредством конического сечения. Содержание 1 Эллипс 2 Парабола 3 Гипербола … Википедия
Эрос (малая планета № 433) — Эрос (Eros), малая планета № 433, открытая в 1898 любителем астрономии Г. Виттом в Берлине. Э. относится к числу малых планет земной группы, которые в своём движении вокруг Солнца могут близко подходить к Земле. Период обращения Э. вокруг Солнца… … Большая советская энциклопедия
Церера (малая планета №1) — Церера Церера в видимом цвете. Снимок телескопа Хаббла Открытие Первооткрыватель Джузеппе Пьяцци Дата открытия … Википедия
Зена (малая планета) — 136199 Эрида Открытие A Первооткрыватель Майкл Браун, Чедвик Трухильо, Дэвид Рабинович Дата обнаружения … Википедия
Икар (малая планета) — 1566 Икар [[Файл:|275px|]] Открытие A Первооткрыватель Вальтер Бааде Дата обнаружения 27 июня 1949 Альтернативные обозначения … Википедия
Кольцово (малая планета) — 9154 Кольцово [[Файл:|275px|]] Открытие A Первооткрыватель Людмила Черных Дата обнаружения 16 сентября 1982 Альтернативные обозначения … Википедия
Эрис (малая планета) — 136199 Эрида Открытие A Первооткрыватель Майкл Браун, Чедвик Трухильо, Дэвид Рабинович Дата обнаружения … Википедия
Юнона (малая планета № 3) — 3 Юнона [[Файл:|275px|]] Открытие A Первооткрыватель Карл Хардинг Дата обнаружения 1 сентяб … Википедия
Большая полуось
Большая полуось — это один из основных геометрических параметров объектов, образованных посредством конического сечения.
Содержание
Эллипс
Большой осью эллипса называется его наибольший диаметр, прямая проходящая через центр и два фокуса. А большая полуось составляет половину этого расстояния, и таким образом, идёт от центра, через фокус, и на край эллипса. А под углом в 90° к большой полуоси располагается малая полуось — это минимальное расстояние от центра эллипса до его края. Для частного случая круга, большая и малая полуоси равны и являются радиусами. Таким образом, можно думать о большой и малой полуосях как о, своего рода, радиусах эллипса.
Длина большой полуоси 
связана с длиной малой полуоси 
через эксцентриситет 
и коническое сечение 
, следующим образом:
Большая полуось представляет собой среднее значение наибольшего и наименьшего расстояния от точки эллипса до его фокусов. Рассмотрим теперь уравнение в полярных координатах, с точкой в начале координат (полюс) и лучом, начинающейся из этой точки (полярная ось):
Получим средние значения 
и 
и большую полуось 
Парабола
Параболу можно получить как предел последовательности эллипсов, где один фокус остаётся постоянным, а другой отодвигается в назад, сохраняя постоянным. Таким образом и стремятся к бесконечности, причём быстрее, чем .
Гипербола
Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси 
(слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:
Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:
.
Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы. [1]
Астрономия
Орбитальный период
В небесной механике орбитальный период 
обращения малых тел по эллиптической или круговой орбите вокруг более крупного центрального тела рассчитывается по формуле:
— это размер большой полуоси орбиты 
— это стандартный гравитационный параметр (en:standard gravitational parameter)
Следует обратить внимание, что в данной формуле для всех эллипсов период обращения определяется значением большой полуоси, независимо от эксцентриситета.
Для объектов Солнечной системы большая полуось связана с орбитальным периодом по третьему закону Кеплера.
— орбитальный период в годах; — большая полуось в астрономических единицах.
Это выражение является частным случаем общего решения задачи двух тел Исаака Ньютона:
— гравитационная постоянная 
— масса центрального тела 
— масса обращающегося вокруг него спутника. Как правило, масса спутника настолько мала по сравнению с массой центрального тела, что ею можно пренебречь. Поэтому, сделав соответствующие упрощения в этой формуле, получим данную формулу в упрощённом виде, который приведён выше.
Орбита движения спутника вокруг общего с центральным телом центра масс (барицентра), представляет собой эллипс. Большая полуось используется в астрономии всегда применительно к среднему расстоянию между планетой и звездой, в результате орбиты планет Солнечной системы приведены к гелиоцентрической системе, а не к системе движения вокруг центра масс. Эту разницу удобнее всего проиллюстрировать на примере системы Земля-Луна. Отношение масс в этом случае составляет 81,30059. Большая полуось геоцентрической орбиты Луны составляет 384400 км. В то время как расстояние до Луны относительно центра масс системы Земля-Луна составляет 379700 км, из-за влияния массы Луны центр масс находится не в центре Земли, а в 4700 км от него. В итоге средняя орбитальная скорость Луны относительно центра масс составляет 1,010 км/с, а средняя скорость Земли 0,012 км/с. А общая сумма этих скоростей даёт орбитальную скорость Луны 1,022 км/с; тоже самое значение можно получить, рассматривая движение Луны относительно центра Земли, а не центра масс.
Среднее расстояние
Часто говорят, что большая полуось является средним расстоянием между центральным и орбитальным телом. Это не совсем верно, так как под средним расстоянием можно понимать разные значения – в зависимости от величины, по которой производят усреднение:
Энергия; расчёт большой полуоси методом векторов состояния
В небесной механике большая полуось может быть рассчитана методом векторов орбитального состояния:
для эллиптических орбит
для гиперболической траектории
(стандартный гравитационный параметр), где:
— орбитальная скорость спутника, на основе вектора скорости, 
— вектор положения спутника в координатах системы отсчёта, относительно которой должны быть вычислены элементы орбиты (например, геоцентрический в плоскости экватора — на орбите вокруг Земли, или гелиоцентрический в плоскости эклиптики — на орбите вокруг Солнца), — гравитационная постоянная, и — массы тел.
Большая полуось рассчитывается на основе общей массы и удельной энергии, независимо от значения эксцентриситета орбиты.
См. также
Примечания
Ссылки
 | Это заготовка статьи о науке. Вы можете помочь проекту, исправив и дополнив её. Это примечание по возможности следует заменить более точным. |
| Орбиты | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Основные | Box-орбита • Орбита захвата • Эллиптическая орбита / Высокая эллиптическая орбита • Орбита ухода • Орбита захоронения • Гиперболическая траектория • Наклонная орбита / Ненаклонная орбита • Оскулирующая орбита • Параболическая траектория • Опорная орбита (в т.ч. низкая) • Синхронная орбита • (Полусинхронная • Субсинхронная) • Стационарная орбита |
| Геоцентрические | Геосинхронная орбита • Геостационарная орбита • Солнечно-синхронная орбита • Низкая околоземная орбита • Средняя околоземная орбита • Высокая околоземная орбита • Молния-орбита • Околоэкваториальная орбита • Орбита Луны • Полярная орбита • Тундра-орбита • TLE |
| Вокруг других небесных тел и точек | Ареосинхронная орбита • Ареостационарная орбита • Гало-орбита • Орбита Лиссажу • Окололунная орбита • Гелиоцентрическая орбита • Солнечно-синхронная орбита |
| Классические |  Наклонение ·  Долгота восходящего узла · Эксцентриситет ·  Аргумент перицентра · Большая полуось ·  Средняя аномалия на эпоху |
| Другие |  Истинная аномалия · Малая полуось ·  Эксцентрическая аномалия ·  Средняя долгота · Истинная долгота · Период обращения |
 Небесная механика | |
|---|---|
| Законы и задачи | Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера |
| Небесная сфера | Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость |
| Параметры орбит | Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха |
| Движение небесных тел | Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова |
| Астродинамика | |
| Космический полёт | Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера» |
| Орбиты КА | Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита |
Полезное
Смотреть что такое «Большая полуось» в других словарях:
большая полуось — didysis pusašis statusas T sritis fizika atitikmenys: angl. semi major axis vok. große Halbachse, f rus. большая полуось, f pranc. demi grand axe, m … Fizikos terminų žodynas
большая полуось а — 3.2 большая полуось а: Максимальный радиус эллипсоида. Примечание Для эллипсоида, представляющего Землю, это радиус экватора. Источник: ГОСТ Р 52572 2006: Географические информационные системы. Координатная основа. Общие требования … Словарь-справочник терминов нормативно-технической документации
большая полуось эллипсоида — 2.1.1 большая полуось эллипсоида : Параметр, характеризующий размер эллипсоида. Источник … Словарь-справочник терминов нормативно-технической документации
Большая полуось орбиты — величина (элемент орбиты (См. Элементы орбиты)), определяющая вместе с эксцентриситетом орбиты (См. Эксцентриситет орбиты) её размеры … Большая советская энциклопедия
Большая — постоянное или часто повторяющееся воздействие жидкостей на покрытие пола. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением материалов фирмы «Хенкель Баутехник» … Словарь-справочник терминов нормативно-технической документации
Большая комета 1811 года — C/1811 F1 (Большая комета) Открытие Первооткрыватель: Оноре Флагерье Дата открытия: 25 марта 1811 Альтернативные обозначения: 1811 I 1811a Характеристики орбиты Афелий: 424 а. е. Перигелий: 1,035412 а. е. Большая полуось … Википедия
Большая мартовская комета 1843 года — C/1843 D1 (Большая мартовская комета) Зарисовка Большой мартовской кометы 1843, сделанная в Тасмании. Открытие Дата открытия: 5 февраля 1843 Альтернативные обозначения: 1843 I 1843a Характеристики орбиты Афелий: 129 а. е … Википедия
Большая комета 1843 года — C/1843 D1 (Большая мартовская комета) Зарисовка Большой мартовской кометы 1843, сделанная в Тасмании. Открытие Дата открытия: 5 февраля 1843 Альтернативные обозначения: 1843 I 1843a Характеристики орбиты Афелий: 129 а. е … Википедия
Большая комета 1965 года — C/1965 S1 (Икея Секи) Открытие Первооткрыватель: Каору Икея, Цуоми Секи Дата открытия: 18 сентября 1965 Альтернативные обозначения: 1965 VIII; 1965f Характеристики орбиты Эпоха: 7 октября 1965 … Википедия
Малая полуось — Не следует путать с термином «Эллипсис». Эллипс и его фокусы Эллипс (др. греч. ἔλλειψις недостаток, в смысле недостатка эксцентриситета до 1) геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1… … Википедия