Что такое поляра крыла самолета
Алексей Больнов. Поляра
Часть 1. Определения.
На первый взгляд — мало, что говорящая кривая. Однако уже здесь можно сделать ряд выводов. Первое — из графика видна МИНИМАЛЬНАЯ и МАКСИМАЛЬНАЯ ГОРИЗОНТАЛЬНАЯ скорость крыла. Минимальная скорость соответствует скорости, до которой можно максимально затормозить крыло, — у параплана триммера зажаты до упора, клеванты задавлены до максимально допустимого предела — еще чуть-чуть и получим срыв потока («задний свал»), у других планирующих летальных аппаратов аналогичные действия по достижению минимальной горизонтальной скорости — отдача ручки у дельтапланов, выпуск закрылков и увеличение угла планирования у планеров. Соответственно, на максимальной скорости триммера и клеванты полностью отпущены, при этом акселератор зажат до предела.
Также из графика поляры можно сделать вывод о двух наиболее интересных для практики режимах; это режим МАКСИМАЛЬНОГО качества (используется на экономичных переходах, когда с данной высоты необходимо улететь на максимально возможное расстояние) и режим МИНИМАЛЬНОЙ вертикальной скорости (особенно актуален при обработке слабых восходящих потоков). Режим максимального качества определяется следующим образом — из начала координат проводится касательная к поляре. В общей точке касательной и поляры мы получим скорость МАКСИМАЛЬНОГО качества. На практике этому режиму соответствует, как правило, полностью отпущенные триммера, немного поджатые клеванты для простых куполов или немного выдавленный акселератор для «гоночных» парапланов.
Режим минимального снижения определяется аналогично — проводится горизонтальная касательная к поляре. Ввиду того, что поляра в верхней своей части достаточно полога, то затруднительно определить конкретную точку (в этом вообще-то нет необходимости), в результате получаем, что скорости минимального снижения соответствует набор горизонтальных скоростей. То есть — вертикальной скорости, на которой аппарат снижается меньше всего, соответствует некоторый промежуток горизонтальных скоростей. Получается, что на этом режиме можно в узком диапазоне изменять общую скорость без изменения вертикальной составляющей. На практике — немного задавленные триммера, поджатые клеванты. Именно здесь, при обработке слабых потоков, в первую очередь проявляется опыт пилота и его знание конкретного купола.
Возникает вопрос — а где же расположена точка, которая соответствует ситуации, когда пилот параплана ничего не делает (акселератор и триммера полностью отпущен, клеванты — брошены). Эта точка соответсвует «Балансировочной скорости». На графике она расположена где-то возле точки максимального качества. Где-то более точно определяется для каждого купола в отдельности. К примеру, для большинства относительно простых куполов наибольшее качество получается при чуть поджатых клевантах, то есть «балансировочная» точка расположена после точки максимального качества. В тоже время, для куполов, оптимизированных под скоростные переходы, точка максимального качества находится дальще чем точка «балансировочной скорости».
Подведем итоги (повторение — мать учения):
Часть 2. Применение.
Нисходящий поток. Поляра перемещается вниз на величину, соответствующую скорости потока. При этом скорость наибольшего качества приближается к максимальной скорости крыла.
Встречный ветер. Поляра смещается влево. При скорости ветра превышающего минимальную скорость крыла поляра переходит за вертикальную ось скоростей, соответственно, на режиме минимальной горизонтальной скорости крыло начинает лететь назад. При этом скорость наибольшего качества также, как и при нисходящем потоке, приближается к максимальной скорости крыла.
Попутный ветер. Поляра смещается вправо. При увеличении скорости ветра скорость максимального качества приближается к скорости минимального снижения. Получаем ситуацию аналогичной режиму полета в восходящем потоке.
Аэродинамические характеристики крыла самолета
ВСЯКАЯ несущая поверхность, помимо сопротивления, создает еще подъемную силу, обеспечивающую полет летательного аппарата. Единый поток перед крылом разделяется на два неодинаковых потока (рис. 1,а). В верхнем потоке струйки как бы сжимаются, скорость их увеличивается, в нижнем же потоке, наоборот, струйки расширяются и скорость их уменьшается. По закону Бернулли, чем выше скорость, тем меньше давление в струе. Следовательно, над крылом образуется область, давление в которой ниже, чем под крылом.
В зависимости от скорости распределяется и давление по крылу (рис. 1,б). Каждый вектор давления на диаграммах представляет собой силу, которая действует на единицу площади поверхности крыла. Если все эти силы сложить, то получим полную аэродинамическую силу, воздействующую на крыло. Исключением в этом случае будут силы трения, которые по диаграмме распределения давления определить нельзя, так как они направлены по касательной к профилю.
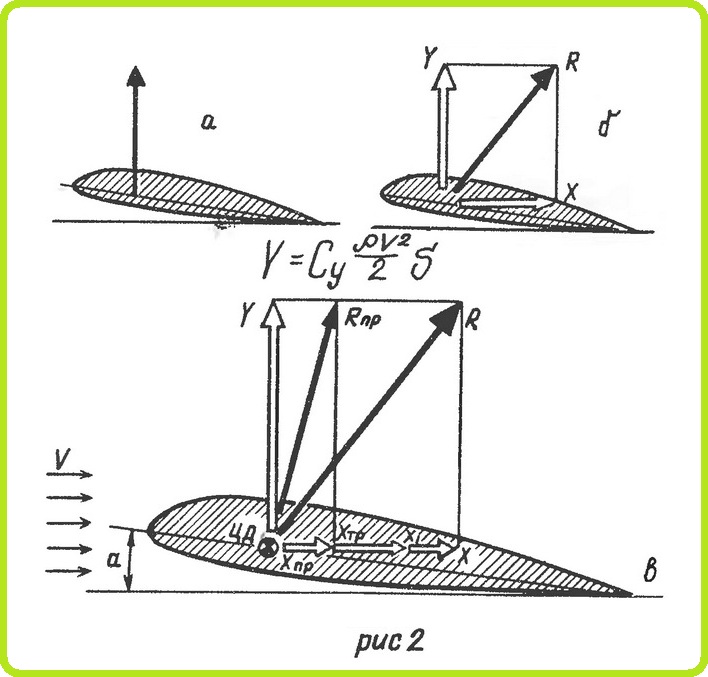
Проекция полной аэродинамической силы на ось, перпендикулярную направлению потока, называется подъемной силой (рис. 2,а). Полную аэродинамическую силу R можно разложить на подъемную силу Y и силу лобового сопротивления X (рис. 2,б.)
Подъемная сила крыла зависит от его геометрических размеров, положения относительно потока, скорости полета модели, плотности воздуха и несущей способности профиля крыла. Эту зависимость принято записывать в виде формулы:
где Cy — коэффициент подъемной силы крыла, учитывающий несущую способность профиля.
Этот коэффициент зависит от формы профиля и угла атаки α — угла между скоростью набегающего воздушного потока и хордой профиля (рис. 2в). Хорда профиля — это условная прямая линия, применяемая для построения профиля, проходящая, как правило, через носик и хвостовик профиля.
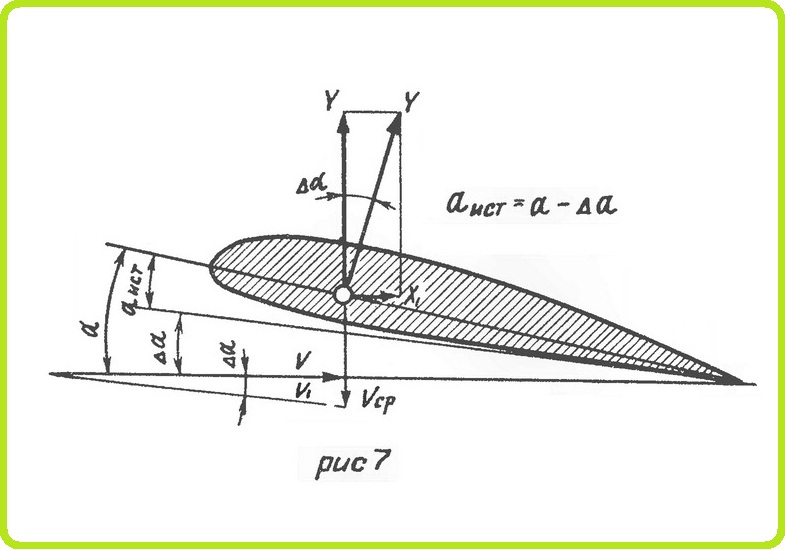
Кроме сопротивления трения и формы, в коэффициент Cx входит еще один третий вид сопротивления — индуктивное. Дело в том, что крыло отбрасывает набегающий на него поток воздуха вниз со скоростью Vcp (рис. 7) так, что в итоге он направлен не по скорости v, a по скорости v1. Это явление называется скосом потока. Угол отклонения потока ∆α называется углом скоса потока. Сложив геометрически скорости V и Vcp. получают действительное направление и величину скорости потока v1, обтекающего крыло. Изменение направления скорости вызывает, естественно, и изменение угла атаки
Благодаря скосу потока истинный угол атаки меньше геометрического. Угол скоса потока определяется по формуле
где λ — удлинение крыла.
Удлинение крыла λ определяется как отношение квадрата размаха крыла L к площади крыла Sкр
Размах крыла L определяется как расстояние между двумя плоскостями, параллельными плоскости симметрии и касающимися концов крыла.
Подъемная сила всегда направлена перпендикулярно к потоку, обтекающему крыло. Благодаря скосу потока подъемная сила отклонится назад на угол ∆α и будет перпендикулярна новому направлению скорости V1
Эта подъемная сила называется истинной. Ее можно разложить на две составляющие: перпендикулярную к направлению скорости полета V и параллельную направлению скорости. Эта составляющая, существование которой возможно только при наличии подъемной силы, направлена всегда против движения крыла.
Коэффициент индуктивного сопротивления определяют по формуле
Угол скоса потока и индуктивное сопротивление зависят от формы профиля крыла, удлинения и от угла атаки.
Таким образом, полное лобовое сопротивление крыла конечного размаха состоит из сопротивления формы, сопротивления трения и индуктивного сопротивления (рис. 2в). Соответственно, коэффициент сопротивления крыла выражается формулой
Точка приложения полной аэродинамической силы называется центром давления. Условились считать, что центр давления лежит на хорде крыла. Если характер обтекания правой и левой половины крыла одинаков, центр давления всего крыла лежит в плоскости симметрии. Нарушение геометрической и аэродинамической симметрии крыла вызовет смещение центра давления.
Положение центра давления на хорде зависит от угла атаки и оказывается различным у профилей разной формы. Характер перемещения центра давления вдоль хорды при изменении угла атаки зависит от формы профиля.
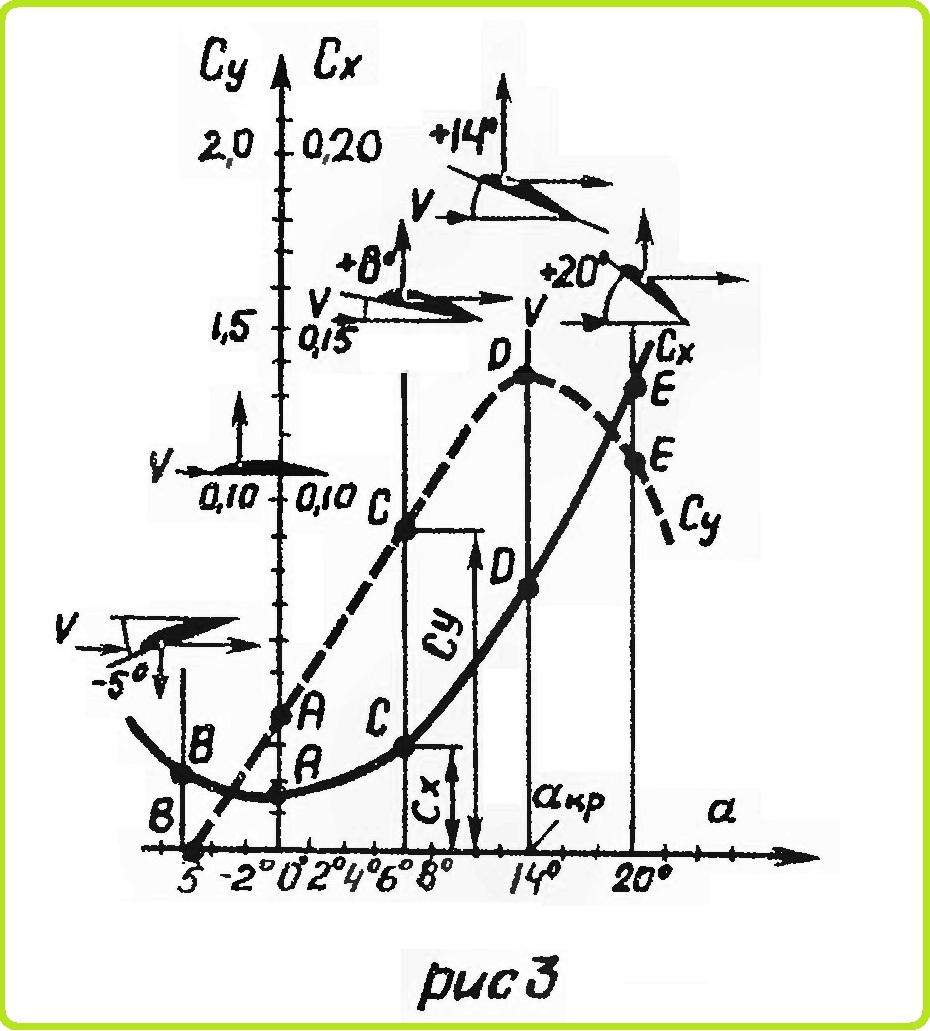
В этом отношении профили делятся на три категории. У несимметричных 1,2 и вогнуто-выпуклых 3,4 профилей (рис. 4), у которых средняя линия вогнута, центр давления при увеличении угла атаки перемещается вперед и наиболее переднее положение занимает при α, близких к αкр, В этом случае центр давления находится примерно на расстоянии 25—35% хорды от носика профиля. При уменьшении угла атаки он перемещается назад и при углах атаки, на которых Су становится близким к Су = 0, уходит за пределы крыла.
У симметричных профилей 4, имеющих прямую среднюю линию, центр давления в пределах значительного диапазона углов атаки занимает постоянное положение и находится примерно на расстоянии 25% длины хорды от носика. При углах атаки больших критического, центр давления у них резко уходит назад.
У S-образных профилей 6 отогнута вверх задняя кромка. Если хвостик профиля отогнут мало, то перемещение центра давления такое же, как и у профилей первой категории. Бели хвостик отогнут больше, то профиль будет иметь постоянный центр давления. Если же его отогнуть еще больше, то центр давления при увеличении угла атаки отходит назад.
Перемещение центра давления вызывает изменение момента равнодействующей воздушных сил относительно центра тяжести модели. Для того, чтобы судить об устойчивости крыла данного профиля, необходимо знать, как меняется момент воздушных сил, действующих на крыло, с изменением угла атаки.
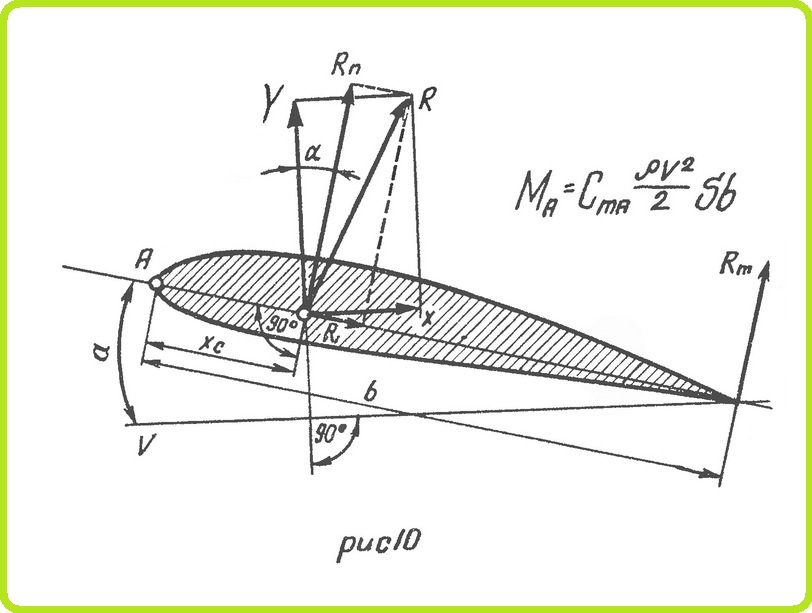
На рис. 10 изображен профиль крыла модели. Так как при предварительных расчетах конструкция модели еще неизвестна, и, следовательно, неизвестно положение ее центра тяжести, вращение крыла рассматривают не относительно центра тяжести, а относительно точки А, находящейся на носике профиля. Силу R раскладывают не на Y и X, как это делалось раньше, а на силы Rn и Rt.
Сила Rn мало отличается от Y, поэтому с небольшой ошибкой можно допустить, что Rn = Y. Момент силы Rn относительно точки А равен
где Хс— расстояние от центра давления до точки А.
Так как положение центра давления при разных углах атаки неизвестно, то считают, что крыло вращается силой Rm. приложенной на задней кромке профиля. Для этого необходимо, чтобы
Это равенство может сохраняться при разных углах атаки, так как изменение Y и Хс может соответствовать изменению Rm при постоянном плече b. Величину Rm определяют в аэродинамической трубе из условия равновесия относительно опоры весов. При этом замеряют силу Rm при разных углах атаки. Зная момент, нетрудно подсчитать и коэффициент CmA в формуле
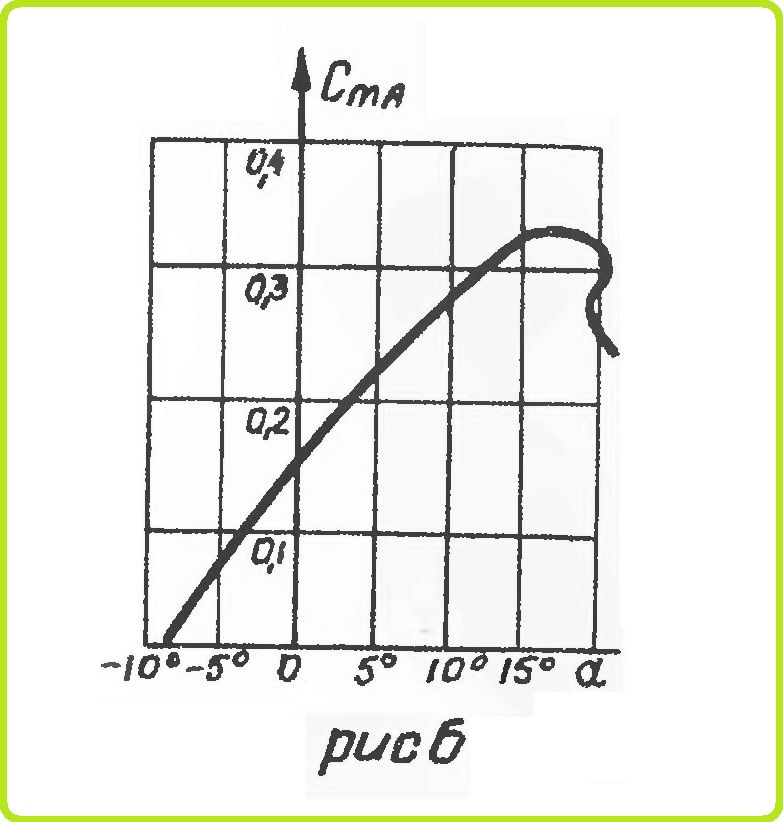
Зависимость коэффициента CmA от угла атаки α представлена на рис. 6.
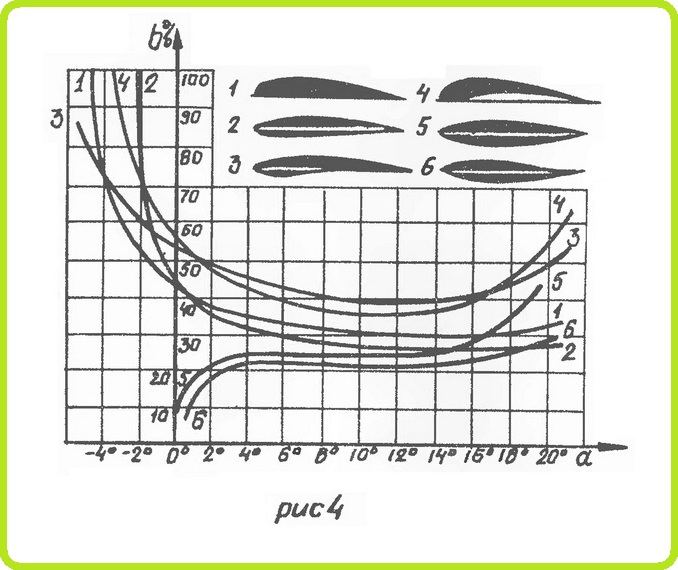
Значение коэффициентов Сх и Су для различных углов атаки — на рис. 3. Значения коэффициентов Су для различных профилей — на рис. 5. Кривая Су по α для симметричного профиля проходит через начало координат. С увеличением вогнутости профиля кривая зависимости Су по α смещается вверх.
Объединенный график зависимости Су от Сх при различных α называется полярой (рис. 8). Имея поляру, можно определить ряд величин, которые характеризуют крыло. Если провести касательную к поляре, параллельную оси Сх, то в точке касания получают угол атаки, соответствующий Су max (рис. 8). Этот угол называется критическим углом атаки «Крит- При увеличении угла атаки сверх критического нарушается обтекание крыла и подъемная сила уменьшается.
Наивыгоднейшим называется такой угол атаки, при котором отношение коэффициента подъемной силы к коэффициенту лобового сопротивления наибольшее. Чтобы найти этот угол, нужно из начала координат провести касательную к поляре.
Отношение подъемной силы к лобовому сопротивлению называют аэродинамическим качеством крыла.
При полете на угле атаки, имеющем Кmax модель проходит наибольшее расстояние. Для того, чтобы модель продержалась наибольшее время в воздухе, необходимо, чтобы угол атаки был равен экономическому углу.
Угол атаки нулевой подъемной силы α0 лежит на пересечении поляры с осью Сх. При этом угле атаки Су = 0.
Угол атаки, при котором Сх имеет наименьшее значение Сх min находится в точке касания линии к поляре, проведенной параллельно оси Су.
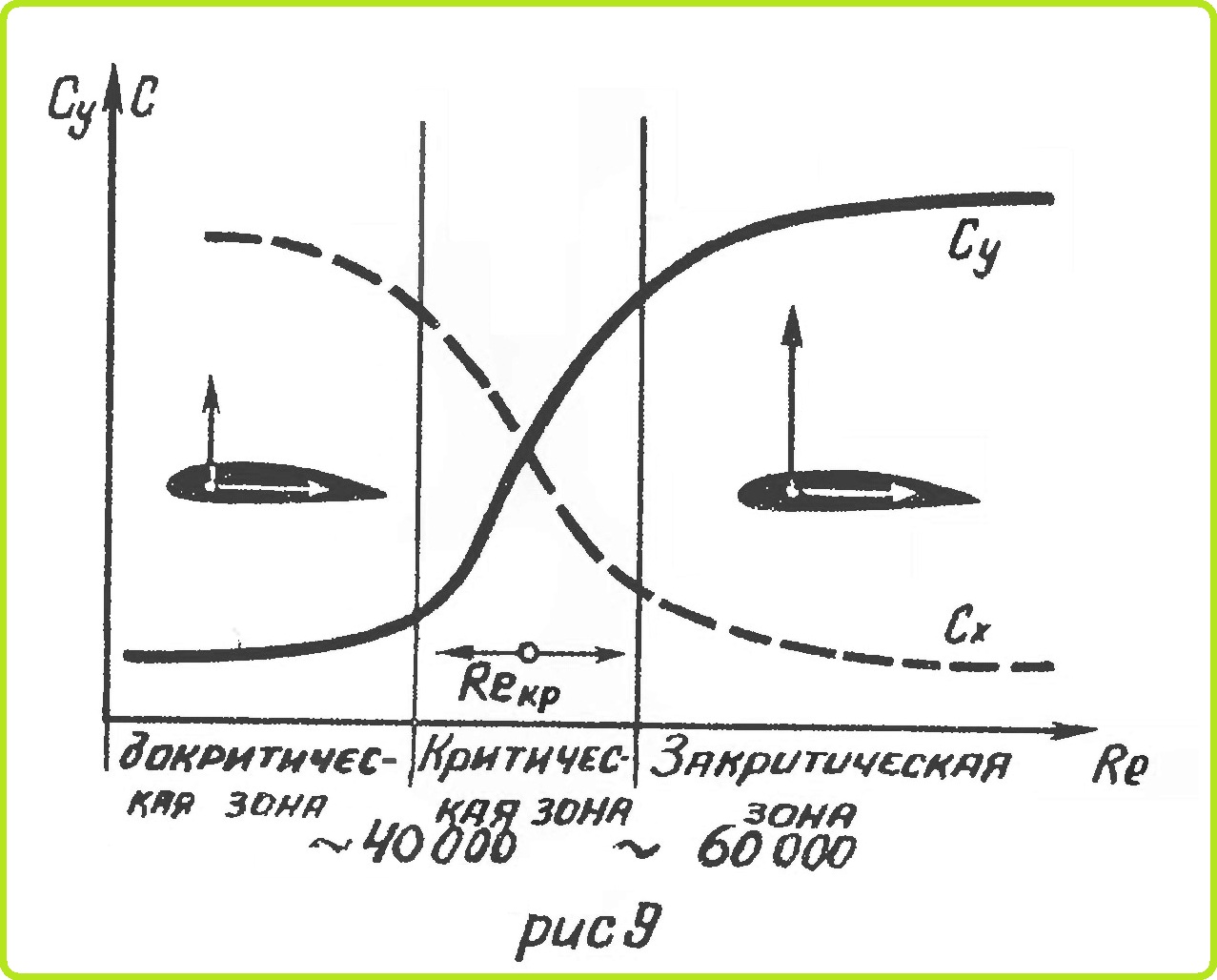
Значения коэффициентов Сх и Су при каком-либо значении угла атаки зависит от числа Re (рис. 9). При Re Reкpит обтекание профиля потоком турбулентное. Благодаря перемешиванию относительная скорость и кинетическая энергия частиц воздуха вблизи профиля более высокая, чем у ламинарного пограничного слоя, и турбулентный пограничный слой может преодолевать повышенное давление на значительном участке задней поверхности профиля. Точка отрыва турбулентного пограничного слоя лежит вблизи задней кромки и тем ближе к ней, чем меньше перепад давления между соседними точками профиля и чем большую скорость имеет внешний поток. Это приводит к росту Су и уменьшению Сх.
Н. ЛЯШЕНКО, руководитель заводского клуба юных техников Харьков
Что такое поляра крыла самолета
5.7. Аэродинамические характеристики самолета
   В общем случае при полете самолета (при наличии угла атаки α и угла скольжения β) вектор полной аэродинамической силы самолета Ra ориентирован в пространстве произвольным образом. В соответствии с записанным ранее выражением для полной аэродинамической силы проекции ее на оси скоростной системы координат можно записать в следующем виде:
 |
 |
 |
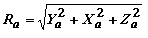 |
 |
   Физический смысл коэффициентов CYa, CXa, CZa аналогичен физическому смыслу коэффициента полной аэродинамической силы CRa .
   Составляющие ( CYa, CXa и CZa ) безразмерного коэффициента полной аэродинамической силы CRa и положение точки ее приложения (центр давления) полностью описывают аэродинамические характеристики самолета.
   В установившемся полете без скольжения (β=0) боковая сила отсутствует, поэтому, естественно,
 |
 |
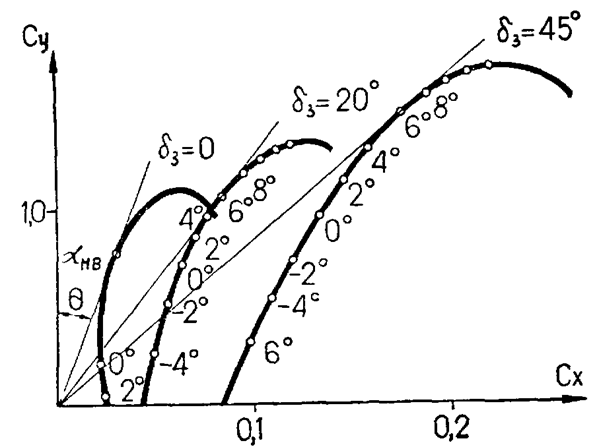
    Обычно принято представлять аэродинамические характеристики самолета в виде зависимостей составляющих коэффициента полной аэродинамической силы ( CYa и CXa ) от полетных углов (α и β). Примерные зависимости CYa(α) и CXa (α) приведены на рис. 5.31.
 |
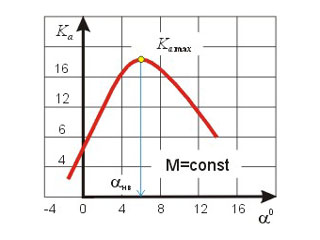 |
   На основании поляры самолета можно построить зависимость аэродинамического качества от угла атаки (рис. 5.34).
   Значения аэродинамических коэффициентов существенным образом зависят от скорости (числа М) полета. Для скоростей полета, соответствующих M ¥ ¥ ³ Mкрит, к этому сопротивлению добавляется волновое сопротивление.
   В общем виде
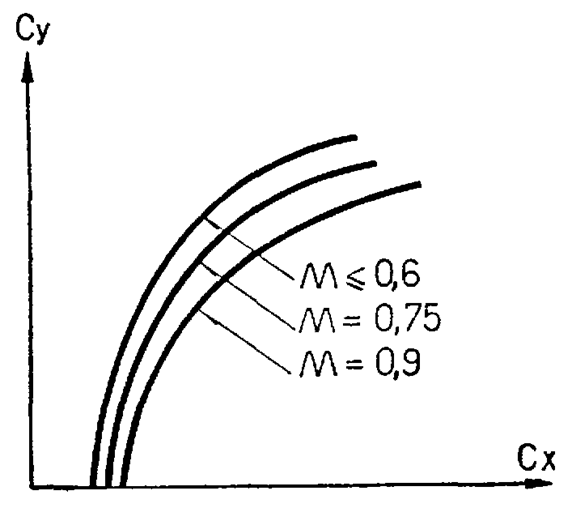
Рис. 5.35. Зависимость аэродинамических коэффициентов прямого крыла от числа М (пример)
   До чисел М £ 0,4 значения всех аэродинамических коэффициентов практически постоянны, так как сжимаемость воздуха в потоке не проявляется.
   С ростом скорости до соответствующей Mкрит увеличение коэффициента C α Ya происходит из-за проявления сжимаемости и увеличения зоны разрежения над крылом; коэффициент CXaо медленно растет из-за увеличения зоны повышенного давления перед крылом.
   В диапазоне чисел М от Mкрит до М=1 увеличение C α Ya замедляется из-за образования местной сверхзвуковой зоны и прямого скачка уплотнения над крылом и достигает максимума к моменту появления местной сверхзвуковой зоны и скачка уплотнения под крылом. С дальнейшим ростом скорости происходит сначала уменьшение до минимума, а затем опять увеличение коэффициента C α Ya, так как смещаются к задней кромке скачки уплотнения сначала на нижней, а затем на верхней поверхности крыла, что сопровождается соответствующим увеличением зон разрежения на этих поверхностях. Увеличение коэффициента C α Ya прекращается с появлением головного прямого отсоединенного скачка при М=1.
   Одновременно резко увеличивается коэффициент лобового сопротивления в связи с развитием волнового кризиса; коэффициент CXaо достигает максимального значения при М=1 вследствие появления головного прямого отсоединенного скачка.
   В диапазоне чисел M>1 с ростом сверхзвуковой скорости головной скачок уплотнения приближается к передней кромке, приобретая форму косого, затем скачок становится присоединенным, углы наклона скачков уменьшаются, соответственно уменьшаются зоны возмущений на верхней и нижней поверхностях профиля, что приводит к уменьшению коэффициентов C α Ya и CXaо.
   Резкое увеличение лобового сопротивления (рис. 5.35, 5.36) и, соответственно, уменьшение качества самолета (рис. 5.37) требуют для полета со скоростями, соответствующими M >Mкрит (преодоления так называемого «звукового барьера» ), значительного увеличения тяги двигателя P.
   Напомним, что для совершения горизонтального полета необходимо выполнить условия:
 |
 |
   Отсюда потребная для горизонтального полета тяга двигателя
   Самолеты с прямым крылом и поршневыми двигателями с воздушными винтами не могли не только достигнуть скоростей полета, соответствующих M ³ 1, но даже и приблизиться к таким скоростям.
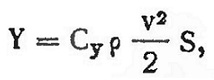
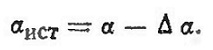
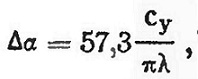
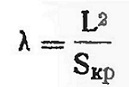
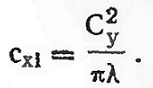
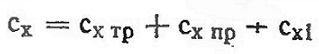
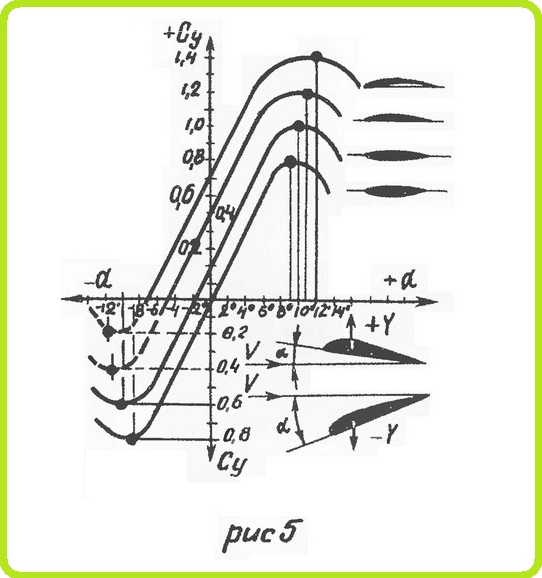
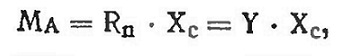
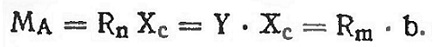
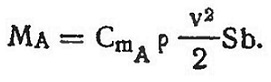
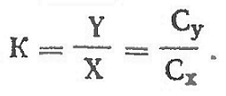
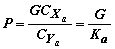



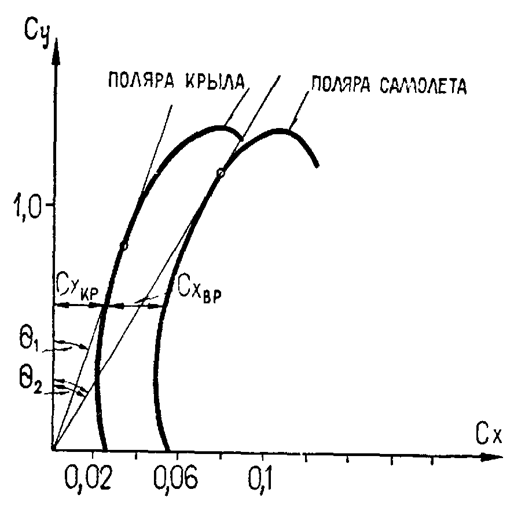
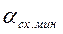 ) находится проведением параллельно оси Сy касательной к поляре. При полете на этом угле атаки будут наименьшие потери на сопротивление. На этом угле атаки (или близком к нему) совершается полет с максимальной скоростью.
) находится проведением параллельно оси Сy касательной к поляре. При полете на этом угле атаки будут наименьшие потери на сопротивление. На этом угле атаки (или близком к нему) совершается полет с максимальной скоростью.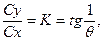 (28)
(28)
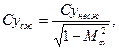 (29)
(29)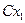 в дозвуковом потоке сжимаемого газа увеличится пропорционально
в дозвуковом потоке сжимаемого газа увеличится пропорционально 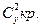 Аэродинамическое качество самолета с момента заметного проявления эффекта сжимаемости начинает уменьшаться.
Аэродинамическое качество самолета с момента заметного проявления эффекта сжимаемости начинает уменьшаться.