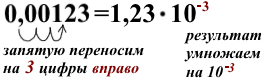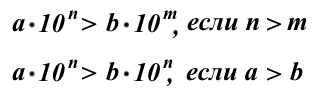Что такое порядок числа в алгебре 7 класс
Стандартный вид числа
Стандартный вид числа — это его запись в виде произведения
Число n называется порядком числа, записанного в стандартном виде.
В стандартном виде можно записать любое положительное число.
Как правило, стандартный вид числа используют для записи больших и малых величин.
Записать число в стандартном виде и указать порядок числа:
Чтобы записать число в стандартном виде, надо представить его в виде произведения, первый множитель которого — число от единицы до десяти (1≤a
Получили число, записанное в стандартном виде. Его порядок n=6.
При решении примеров на приведение числа к стандартному виду удобнее деление числа на
заменить умножением на
Итак, для приведения к стандартному виду числа, больше либо равного 10, запятую в его записи переносим влево на n цифр и результат умножаем на 10 в степени n:
2) 12 346 000 000=12 346 000 000,
Чтобы величина первого множителя входила в промежуток от 1 до 10, надо запятую в записи данного числа перенести на 10 знаков влево, а чтобы число не изменилось, умножить результат на 10¹º:
Это число записано в стандартном виде. Его порядок n=10.
Чтобы первый множитель соответствовал условию 1≤a
Число 5430 представляем в стандартном виде. Для этого запятую в его записи переносим на 3 цифры влево и результат умножаем на 10³.
Далее выполняем умножение степеней с одинаковыми основаниями.
Сравнение чисел, записанные в стандартном виде

так как порядок первого числа больше порядка второго числа (8>7);
поскольку порядок первого числа меньше порядка второго числа (-8 
так как при равных порядках первый множитель у первого числа больше, чем у второго (3,4>2,97).
Cтандартный вид числа
В задачах по физике часто приходится работать с очень большими и очень малыми величинами.
Как вести вычисления в атомной физике? Или записать радиус электрона? Если потребуется сравнить массу электрона и массу планеты Земля, как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?
Физики и математики, столкнувшись с такими задачами, поняли, что для решения подобных задач требуется привести числа к единому стандартному виду. Так появилось понятие стандартный вид числа.
Прежде чем переходить к объяснению, как записать число в стандартном виде, нужно вспомнить определение степени. Особенно хорошо нужно помнить, чему равняется число « 10 » в различных степенях.
Вспомним, что при умножении целого числа на 10, 100, 1000 и т.д. мы просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..
Теперь запишем тоже самое, используя определение степени.
При делении целого числа на 10, 100, 1000 и т.д. мы убирали нули.
С помощью степени можно записать вычисления выше следующим образом:
С помощью определения отрицательной степени можно записать вычисления выше следующим образом:
Стандартный вид числа
Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.
Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:
Такая запись называется — стандартный вид числа.
При этом число « n » называют порядком числа « a ».
Теперь к примеру. Пусть нам дано число « 5 600 » и требуется записать его в стандартном виде.
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».
В числе « 5 600 » первая цифра справа — « 5 ». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.
Теперь запишем « 1000 » с использованием степени.
Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.
Таким образом « 5 600 » в стандартном виде будет выглядеть следующим образом:
Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно. Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.
Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь « 0,017 ».
Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от « 1 » до « 9 ».
В десятичной дроби « 0,017 » вначале идет « 0 ». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от « 0 ».
Это цифра « 1 ». Посчитаем сколько знаков (цифр) стояло от запятой до цифры « 1 », включая саму цифру « 1 ».
Получается два знака. Начнем записывать « 0,017 » в стандартном виде. Перенесем запятую и поставим ее справа от « 1 ».
Выходит, чтобы из « 1,7 » сделать 0,017 », нужно « 1,7 разделить на « 100 » (чтобы перенести запятую на два знака влево).
Запишем это деление на « 100 », используя обыкновенную дробь.
С помощью отрицательной степени запишем окончательный вид числа « 0,017 » в стандартном виде.
Примеры решения задач
на запись числа в стандартном виде
№ 237 Алимов 8 класс
(Устно) Определить порядок числа, выражающего значение физической константы:
1) масса покоя электрона
me = 9,1093897 · 10 −31
Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень, в которой стоит « 10 ». В данном примере « 10 » стоит в
степени « −31 ». Значит, порядком массы покоя электрона является « −31 ».
№ 238 Алимов 8 класс
2) постоянная Фарадея
F = 96485,309 Кл/моль;
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от « 1 » до « 9 ».
Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра « 9 ».
Получается « 4 » знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим образом:
Порядком числа « 9,6485309 · 10 4 » является степень, в которой стоит « 10 ». Следовательно, порядок « k = 4 ».
Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:
Завершим решение и запишем окончательный ответ, используя свойство «Произведение степеней».
Что такое порядок числа в алгебре 7 класс
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: 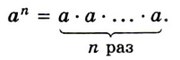
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
а m • а n = а m+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
(а m ) n = а mn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab) n = а n b n
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b) 2 = а 2 + 2аb + b 2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b) 2 = а 2 – 2аb + b 2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а 2 – b 2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а 3 + b 3 = (а + b)(a 2 – аb + b 2 )
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а 3 – b 3 = (а – b)(a 2 + ab + b 2 )
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :
Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Алгебра 7 класс Все формулы
Уравнения
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы 
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
Алгебра 7 класс Все формулы
Функции
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Математика
Числа, подобно единицам, также разделяются на порядки. Так, первые десять чисел называют числами первого порядка. Числа от десяти до ста называют числами второго порядка, от ста до тысячи — числами третьего порядка и т. д.
Названия чисел. При помощи указанных единиц различного порядка мы получаем названия всех остальных чисел. Так, числа, состоящие из одной, двух, трех … единиц второго порядка, или, что то же, одного, двух, трех … десятков, мы называем десять, двадцать (два десять), тридцать, сорок, пятьдесят, шестьдесят, семьдесят, восемьдесят, девяносто. Присоединяя к этим числам девять чисел первого порядка, мы получаем все числа второго порядка. Так, присоединяя к числу десять все числа первого порядка, мы получаем все числа между десятью и двадцатью: одиннадцать, двенадцать (два на десять), тринадцать, четырнадцать, пятнадцать, шестнадцать, семнадцать, восемнадцать, девятнадцать. Присоединяя к двадцати девять чисел первого порядка, получим все числа между двадцатью и тридцатью: двадцать один, двадцать два и т. д. Наибольшее число второго порядка есть девяносто девять.
Десять десятков образуют сотню или сто, единицу третьего порядка. Числа, состоящие из одной или нескольких единиц третьего порядка, мы называем: сто, двести, триста, четыреста, пятьсот, шестьсот, семьсот, восемьсот, девятьсот.
Присоединяя к этим числам все числа первого и второго порядка, мы получаем все числа третьего порядка, например, восемьсот сорок пять, девятьсот четыре. Наибольшее число третьего порядка есть девятьсот девяносто девять.
Десять сот образуют тысячу — единицу четвертого порядка. Повторяя тысячу один, два и т. д. раз, образуем числа: тысяча, две тысячи, три тысячи и т. д. Присоединяя к этим числам все числа первого, второго и третьего порядков, образуем все числа четвертого порядка и т. д.
Десятичная система. Систему счисления, в которой каждые десять единиц низшего образуют единицу следующего высшего порядка, называют десятичною. Она принята в настоящее время всеми образованными народами.
Основание системы. Число десять называется основанием системы. В основе ее лежит число десять.
Полагают, что число десять принято за основание потому, что первоначально люди считают обыкновенно по пальцам.
Пример. Шесть миллионов пятьсот семь тысяч двести семь есть число седьмого порядка. Оно состоит из шести единиц седьмого прядка (шесть миллионов), к которому присоединено число шестого порядка (пятьсот семь тысяч двести семь).
Число шестого порядка состоит из пяти единиц шестого порядка (пятьсот тысяч), к которому присоединено число четвертого порядка (семь тысяч двести семь).
Число четвертого порядка состоит из семи единиц четвертого порядка (семь тысяч), к которому присоединено число третьего порядка (двести семь).
Число третьего порядка состоит из двух единиц третьего порядка (двести), к которому присоединяется число первого порядка (семь).
Число семь состоит из семи простых единиц.
Всякое число содержится между двумя единицами различных порядков. Всякое число более единицы одного порядка и менее единицы следующего высшего порядка. Так, число триста сорок семь более ста и менее тысячи.