Что такое порядок фильтра
Постановка задачи и способы аппроксимации квадрата АЧХ
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
По форме амплитудно-частотной характеристики (АЧХ) различают следующие типы фильтров:
Примеры квадрата АЧХ для приведенных типов фильтров показаны на рисунке 1.
Полоса частот от 0 до называется полосой пропускания ФНЧ, полоса частот выше называется полосой подавления или полосой заграждения. Полоса частот между и называется переходной полосой фильтра. Мы должны научится регулировать искажения сигнала и подавление при использовании ФНЧ.
Таким образом, получили такой «изогнутый коридор» в который должна поместиться АЧХ нашего фильтра. При этом, чем «коридор уже», тем параметр меньше, а параметр больше.
Принято искажение в полосе пропускания и требуемое подавление фильтра в полосе заграждения выражать в децибелах, как и соответственно. Тогда:
Из (2) можно выразить:
Порядок фильтра можно определить как максимальное количество нулей и полюсов передаточной функции фильтра. Также можно сказать, что порядок фильтра задается максимальной степенью полинома числителя и знаменателя передаточной функции фильтра. Однако для расчета фильтра мы задаем параметры частотной характеристики, в которые должен укладываться наш фильтр, и мы не знаем какой порядок фильтра для этого потребуется.
Мы неслучайно уделяем особое внимание параметрам фильтров нижних частот. Дело в том, что ФНЧ служат прототипом для фильтров других типов (ФВЧ, ПФ и РФ), передаточные характеристики которых можно получить из передаточной характеристики ФНЧ путем алгебраических частотных преобразований. При этом ФНЧ с различными значениями частоты среза также могут быть получены из других ФНЧ путем преобразования частоты.
Поэтому фильтры нижних частот подходят на роль прототипов из которых можно получить все типы фильтров с любыми параметрами квадрата АЧХ. При этом особую роль играют нормированные ФНЧ, у которых частота среза рад/с.
Аппроксимация квадрата АЧХ нормированного фильтра нижних частот представляется в виде:
Для того чтобы квадрат АЧХ фильтра разместился в заданном коридоре необходимо, чтобы выполнялись следующие условия:
Необходимо отметить, что для сужения переходной полосы необходимо увеличивать порядок фильтра, однако при практической реализации от порядка фильтра зависит количество реактивных элементов (емкостей и индуктивностей) в его схеме. В результате, увеличение порядка фильтра приводит к усложнению самого фильтра, удорожанию и что самое важное, фильтр с увеличением порядка становится очень чувствительным к разбросу номиналов его компонент и требует точной прецизионной настройки.
Ось абсцисс на рисунке 3 показана в логарифмическом масштабе.
На рисунке 4 показаны аппроксимирующая функция и квадрат АЧХ нормированного ФНЧ Чебышева первого рода порядка при (неравномерность АЧХ фильтра в полосе пропускания дБ).
Хорошо видно, что в полосе пропускания квадрат АЧХ фильтра Чебышева первого рода совершает равноволновые колебания, в отличии от фильтра Баттерворта. При этом скорость спада АЧХ фильтра Чебышева первого рода за пределами полосы пропускания, выше чем у фильтра Баттерворта.
Можно заметить, что АЧХ фильтра Чебышева первого рода носит колебательный характер в полосе пропускания и максимально-гладкая в полосе заграждения, в то время как АЧХ фильтра Чебышева второго рода наоборот колеблется в полосе заграждения и максимально-гладкая в полосе пропускания. Однако есть еще один класс фильтров АЧХ которых носит колебательный характер как в полосе пропускания, так и в полосе подавления. Это эллиптические фильтры Кауэра.
Параметр (неравномерность АЧХ фильтра в полосе пропускания дБ), а параметр задает уровень подавления в полосе заграждения равный дБ. Обратите внимание, что квадрат аппроксимирующей функция эллиптического фильтра показан показан на двух графиках. На верхнем графике показан в масштабе от 0 до 400. Из верхнего графика видно, что имеет полюсы при 1″/> рад/c, что приводит к пульсация квадрата АЧХ фильтра в полосе заграждения. На нижнем графике показаны колебания аппроксимирующей функции в полосе пропускания.
Фильтр Баттерворта обладает самой широкой переходной полосой среди всех фильтров, но у него максимально-гладкая АЧХ. Внесение в АЧХ фильтра Баттерворта колебаний приводит к фильтрам Чебышева, переходная полоса которых у́же чем у фильтра Баттерворта. Равноволновые колебания в полосе пропускания приводят к фильтрам Чебышева первого рода, а равноволновые колебания в полосе заграждения к фильтрам Чебышева второго рода. Внесение равноволновых колебаний как в полосу пропускания, так и в полосу заграждения АЧХ приводит к эллиптическому фильтру с минимальной переходной полосой.
Порядок нормированного ФНЧ Баттерворта рассчитывается из уравнения:
Порядок эллиптического фильтра можно рассчитать из уравнения:
В таблице 1 приведены порядки нормированных ФНЧ Баттерворта, Чебышева и эллиптического для некоторых значения параметров квадрата АЧХ.
Из таблицы 1 видно, что сужение переходной полосы, когда приближается к и уменьшение неравномерности в полосе пропускания с одновременным ростом подавления в полосе заграждения, приводит к очень резкому росту требуемого порядка фильтра Баттерворта. При этом порядок фильтра Чебышева растет медленнее, однако и ему далеко до эллиптического фильтра, который обеспечивает минимальный порядок при заданном коридоре АЧХ.
Переход от фильтра Баттерворта к фильтру Чебышева позволяет сократить порядок фильтра более чем в 5 раз, а использование эллиптического фильтра более чем в 10 раз. В результате, вместо фильтра Баттерворта 118 порядка можно поставить эллиптический фильтр всего 8-го порядка без ухудшения характеристик фильтра. Но это потребует более точной настройки параметров емкостей и индуктивностей при реализации фильтра.
В данном разделе мы рассмотрели постановку задачи расчета аналогового нормированного ФНЧ и произвели анализ различных способов аппроксимации АЧХ фильтра: аппроксимация по Баттерворту, по Чебышеву и по Кауэру. Получили решения уравнения порядка фильтра при заданном коридоре АЧХ для всех перечисленных способов аппроксимации фильтра. Произведен сравнительный анализ порядоков фильтров Баттерворта, по Чебышева и по Кауэра (эллиптического) для некоторых коридоров АЧХ.
Показано, что при сужении коридора АЧХ (сужение переходной полосы, уменьшении неравномерностей в полосе пропускания и увеличении подавления в полосе заграждения) использование эллиптического фильтра приводит к наименьшему требуемому порядку фильтра.
Данные для построения рисунков данного раздела были просчитаны при использовании библиотеки DSPL-2.0
Опции темы
Поиск по теме
Отображение
Кроссоверы— это устройства в звуковых системах, которые создают нужные рабочие частотные диапазоны для динамиков. Динамики сконструированы таким образом, чтобы работать в определенном частотном диапазоне. Они не приемлют частоты, не входящие в эти рамки. Если на высокочастотный динамик (твитер) подать низкую частоту, то звуковая картина испортится, а если сигнал еще и мощный, то твитер «сгорит». Высокочастотные динамики должны работать только с высокими частотами, а низкочастотные динамики должны получить от общего звукового сигнала только низкочастотный диапазон. Оставшаяся средняя полоса достается среднечастотным динамикам (мидвуферы). Следовательно, задача кроссоверов заключается в разделении звукового сигнала на нужные (оптимальные) частотные полосы для соответствующих типов динамиков.
Кроссоверы четвертого порядка. Кроссоверы Баттерворта четвертого порядка имеют высокую чувствительность равную 24 дБ на октаву, что резко уменьшает взаимовлияние динамиков в области разделения частот. Сдвиг по фазе составляет 360 градусов, что фактически означает его отсутствие. Однако величина фазового сдвига в данном случае непостоянна и может привести к неустойчивой работе кроссовера. Эти кроссоверы практически не применяются на практике.
Оптимизировать конструкцию кроссовера четвертого порядка удалось Линквицу и Рили. Данный кроссовер состоит из двух последовательно соединенных кроссоверов Баттерворта второго порядка для твитера, и тоже самое для басового динамика. Чувствительность их также равна 24 дБ на октаву, однако уровень выходного сигнала на каждом фильтре меньше на 6 дБ, чем уровень выходного сигнала кроссовера. Кроссовер Линквица-Рили не имет фазовых сдвигов и позволяет проводить временную коррекцию для динамиков, не работающих в одной физической плоскости. Эти кроссоверы по сравнению с другими конструкциями дают самые лучшие акустические характеристики.
Конструирование пассивных кроссоверов
Пассивные и активные кроссоверы
Настройка активного кроссовера
В этой таблице приведены начальные величины частот среза для различных типов динамиков при настройке активных кроссоверов.
Коэффициенты (Coefficients) – см. Коэффициенты фильтра (Filter Coefficients).
Коэффициенты фильтра (Filter Coefficients) – набор постоянных, также называемых весами элементов (tap weights), используемые при фильтрации сигнала цифровым фильтром. Проектирование цифрового фильтра – это задача определения коэффициентов фильтра, которые бы обеспечивали желаемую частотную характеристику. Для КИХ-фильтра по определению коэффициенты являются значениями импульсной характеристикой фильтра.
Относительное затухание (Relative Attenuation) – затухание, измеренное относительно наибольшего значения амплитуды. Наибольший уровень сигнала (минимальное затухание) обычно задается относительно уровня в 0 ДБ, при этом остальные значения амплитуды на кривой частотной характеристики имеют отрицательные значения (в ДБ).
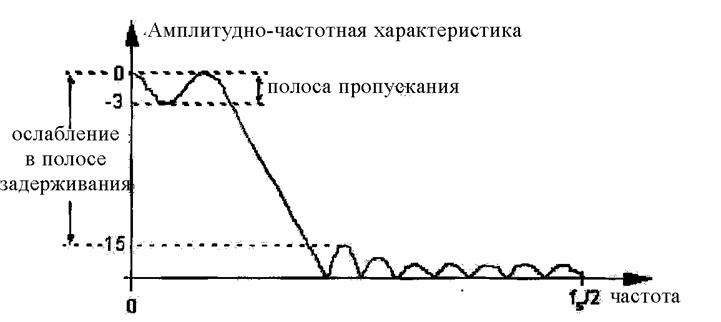
Переходная область (Transition Region) – область частот между полосой пропускания и полосой задерживания цифрового фильтра. Рисунок 4 иллюстрирует переходную область для фильтра нижних частот. Иногда переходная область также называют переходной полосой (transition band).
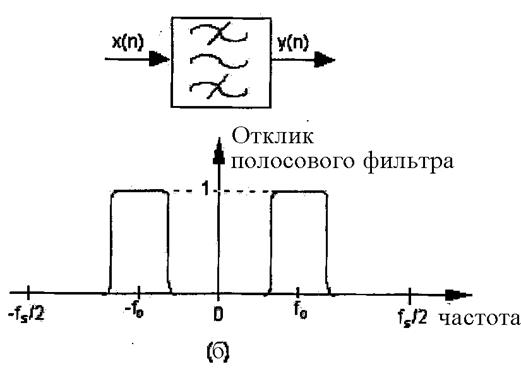
Полосовой фильтр (Bandpass Filter) – фильтр, изображенный на рис.5, который пропускает одну полосу частот и ослабляет частоты выше и ниже этой полосы.
Порядок фильтра (Filter Order) – число, описывающее самый высокий показатель степени числителя или знаменателя передаточной функции цифрового фильтра. Для КИХ-фильтров – знаменателя передаточной функции нет и порядок фильтра – это просто число элементов, входящих в структуру фильтра. Для БИХ-фильтров – порядок фильтра равен числу элементов задержки в структуре фильтра. Как правило, чем выше порядок фильтра, тем лучше АЧХ фильтра.
Пульсации (Ripple) – Пульсации показывают колебания в полосе пропускания или полосе задерживания на кривой амплитудно-частотной характеристики фильтра в дБ. Эллиптические фильтры или фильтры Чебышева имеют равно-волновые характеристики, то есть пульсации (колебания) постоянны по амплитуде во всей их полосе пропускания. Производные от АЧХ фильтров Бесселя и Баттерворта не имеют пульсаций в полосе пропускания. Пульсации в полосе задерживания иногда называют также внеполосными пульсациями (out-of-band ripple).
Пульсации в полосе пропускания (Passband Ripple) – пульсации или колебания амплитудно-частотной характеристики в пределах полосы пропускания фильтра. Неравномерность в полосе пропускания, измеряемая в дБ, проиллюстрирована на рисунке 4. (См. Неравномерность (Ripple)).
Рис. 4. Частотная характеристика цифрового фильтра низких частот, с обозначением неравномерности в полосе пропускания и ослабления в области непропускания.
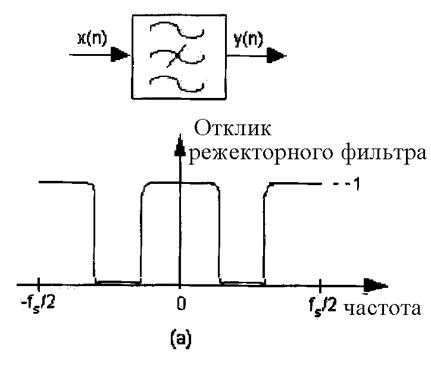
Режекторный фильтр (полосно – заграждающий фильтр, Band Reject Filter) – это фильтр, который ослабляет одну полосу частот и пропускает полосы частот ниже и выше её. Рис.5 изображает частотную характеристику идеального режекторного фильтра. Этот тип фильтра иногда называют также узкополосным режекторным фильтром (фильтр-пробка, notch filter).
Рис. 5 Обозначение фильтров и их частотные отклики (a) Режекторный фильтр; (б) Полосовой фильтр.
Спад (Rolloff) – этот термин используется для описания крутизны, или наклона, характеристики фильтра в области перехода от полосы пропускания к полосе задерживания. О некоторых цифровых фильтрах говорят, что они имеют спад 12 ДБ/октава – имеется в виду, что первая октава от частоты f 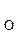
Структурная схема (Structure) – этот термин, используемый в цифровой обработке сигналов. Относится к блок-схеме, показывающей как устроен цифровой фильтр. Рекурсивная структура фильтра – такая, в которой имеет место обратная связь и используются предыдущие значения выходного сигнала фильтра вместе с предыдущими значениями входного сигнала для вычисления текущего выходного сигнала. БИХ-фильтры почти всегда описываются при помощи рекурсивной структуры фильтров. Нерекурсивная структура фильтров – такая, в которой при вычислении текущего выходного сигнала используются только предыдущие входные сигналы. КИХ-фильтры почти всегда описываются при помощи нерекурсивной структуры.
Фазочастотная характеристика (Phase Response) – разность фаз для различных частот между входным и выходным синусоидальными сигналами на данной частоте. ФЧХ, иногда называемая фазовой задержкой (phase delay), обычно изображается в виде кривой, показывающей сдвиг фазы фильтра как функцию от частоты.
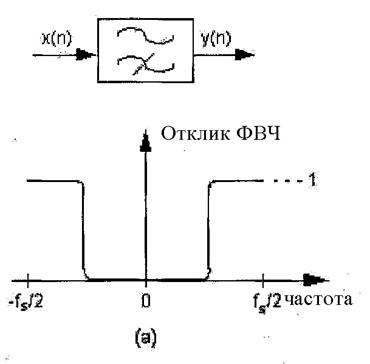
Фильтр верхних частот (ФВЧ, Highpass filter) – фильтр, который пропускает высокие частоты и ослабляет низкие, как показано на рисунке F-5(a).
Рис. 6. Обозначение фильтров и частотные отклики:
Все мы имели возможность ознакомиться с высокочастотной фильтрацией в нашей повседневной жизни. Обратите внимание, что происходит, когда мы усиливаем верхние звуковые частоты (или ослабляем нижние звуковые частоты) на наших домашних стереосистемах. Обычный диапазон частотного отклика звукового усилителя изменяется и дает нам повышенный и резкий (tinny) звук, поскольку подчеркиваются высокочастотные составляющие мелодии.
Чтобы распечатать файл, скачайте его (в формате Word).