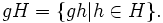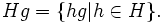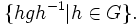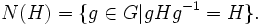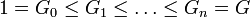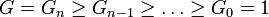Что такое порядок группы

Порядок группы

Для общего описания теории групп см. Группа (математика) и Теория групп.

Курсив обозначает ссылку на этот словарь.

p-группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о примарной группе. Более подробно см. в статье конечная p-группа.

Аддитивная группа кольца ― группа, элементами которой являются все элементы данного кольца, а операция совпадает с операцией сложения в кольце.

Антигомоморфизм групп — отображение групп f : (G,*) → (H,×) такое, что

для произвольных a и b в G (сравните с гомоморфизмом).

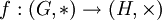
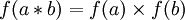
Гомоморфизм групп — отображение групп такое, что

для произвольных a и b в G.

Группа Шмидта — это ненильпотентная группа, все собственные подгруппы которой нильпотентны.

Группа Миллера — Морено — это неабелева группа, все собственные подгруппы которой абелевы.

Групповая алгебра группы G над полем K — это векторное пространство над K, образующими которого являются элементы G, а умножение образующих соответсвует умножению элементов G.

Длина ряда подгрупп — число n в определении ряда подгрупп.

Изоморфизм групп — биективный гомоморфизм.

Изоморфные группы — группы, между которыми существует хотя бы один изоморфизм.

Индекс подгруппы H в группе G — число смежных классов в каждом (правом или левом) из разложений группы G по этой подгруппе H.

Индексы ряда подгрупп — индексы | G_{i + 1}:G_i | в определении субнормального ряда подгрупп.

Класс смежности/смежный класс (левый или правый) подгруппы H в G. Левый класс смежности элемента 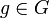по подгруппе H в G есть множество

Аналогично определяется правый класс смежности:

Класс сопряжённости элемента 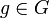есть множество

Коммутант группы есть подгруппа, порождённая всеми коммутаторами группы, обычно обозначается [G,G] или .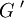

Коммутативная группа. Группа G является коммутативной, или абелевой, если её операция * коммутативна, то есть g*h=h*g .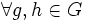

Коммутатор подгрупп — множество всевозможных произведений .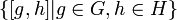

Композиционный ряд группы G — ряд подгрупп, в котором все факторы G_{i + 1} / G_i — простые группы.

Конечная группа — группа с конечным числом элементов.

Конечно определённая группа — группа, обладающая конечным числом образующих и задаваемая в этих образующих конечным числом соотношений.

Конечнопорождённая группа — группа, обладающая конечной системой образующих.

Кручение, TorG, коммутативной или нильпотентной группы G есть подгруппа всех элементов конечного порядка.

Локальная теорема. Говорят, что для некоторого свойства P групп справедлива локальная теорема, если всякая группа, локально обладающая этим свойством, сама обладает им.

Например: локально абелева группа является абелевой, но локально конечная группа может быть бесконечной.

Метабелева группа ― группа, второй коммутант которой тривиален (разрешимая ступени 2).

Метациклическая группа ― группа, обладающая циклической нормальной подгруппой, факторгруппа по которой также циклическая. Всякая конечная группа, порядок которой свободен от квадратов (то есть не делится на квадрат какого-либо числа), является метациклической.

Мультипликативная группа тела ― группа, элементами которой являются все ненулевые элементы данного тела, а операция совпадает с операцией умножения в теле.

Нильпотентная группа — группа, обладающая центральным рядом подгрупп. Минимальная из длин таких рядов называется её классом нильпотентности.

Норма группы — совокупность элементов группы, перестановочных со всеми подгруппами, то есть пересечение нормализаторов всех её подгрупп.

Нормализатор подгруппы H в G — это максимальная подгруппа G, в которой H нормальна. Иначе говоря, нормализатор есть стабилизатор H при действии G на множестве своих подгрупп сопряжениями, то есть

Нормальная подгруппа (инвариантная подгруппа, нормальный делитель). H есть нормальная подгруппа G, если для любого элемента g в G gH = Hg, то есть правые и левые классы смежности H в G совпадают. Иначе говоря, если .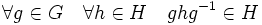

Период группы ― наименьшее общее кратное порядков элементов данной группы.

Периодическая группа ― группа, каждый элемент которой имеет конечный порядок.

Подгруппа — подмножество H группы G, которое является группой относительно операции, определённой в G.

Подгруппа кручения см. кручение.

Для произвольного подмножества S в G, обозначает наименьшую подгруппу G, содержащую S.

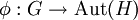
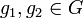
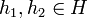
Полупрямое произведение групп G и H над гомоморфизмом (обозначается по разному, в том числе G ⋊_φ H) — множество G × H, наделенное операцией *, для которой (g₁,h₁) * (g₂,h₂) = (g₁φ(h₁)(g₂),h₁h₂) для любых , .

Порядок группы (G,*) — мощность G (то есть число её элементов).

Порядок элемента g группы G — минимальное натуральное число m такое, что g m = e. В случае, если такого m не существует, считается, что g имеет бесконечный порядок.

Простая группа — группа, в которой нет нормальных подгрупп, кроме тривиальной <e> и всей группы.

Примарная группа — группа, все элементы в которой имеют порядок, равный некоторой степени простого числа p (не обязательно одинаковой у всех элементов). Также говорят о p-группе.

Расширение группы — группа, содержащая данную группу в качестве нормальной подгруппы.

Разрешимая группа — группа, обладающая нормальным рядом подгрупп с абелевыми факторами. Наименьшая из длин таких рядов называется её ступенью разрешимости.

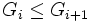
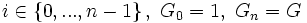
Ряд подгрупп — конечная последовательность подгрупп G₀,G₁. G_n называется рядом подгрупп, если , для всех . Такой ряд записывают в виде

Сверхразрешимая группа — группа, обладающая нормальным рядом подгрупп с циклическими факторами.

Свободная группа, порождённая множеством A — это группа, порождённая элементами этого множества и не имеющая никаких соотношений, кроме соотношений, определяющих группу. Все свободные группы, порождённые равномощными множествами, изоморфны.

Соотношение — тождество, которому удовлетворяют образующие группы (при задании группы образующими и соотношениями).

Факторгруппа группы G по нормальной подгруппе H есть множество классов смежности подгруппы H с умножением, определяемым следующим образом:

Факторы субнормального ряда — фактор-группы G_{i + 1} / G_i в определении субнормального ряда подгрупп.

Холлова подгруппа — подгруппа, порядок которой взаимно прост с её индексом во всей группе.

Центр группы G, обычно обозначается Z(G), определяется как

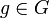
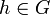
Z(G) = <| gh = hg для любого >,

иначе говоря, это максимальная подгруппа элементов, коммутирующих с каждым элементом G.

Централизатор элемента есть максимальная подгруппа, коммутирующая с этим элементом.

Центральный ряд подгрупп — нормальный ряд подгрупп, в котором 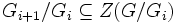, для всех членов ряда.

Циклическая группа — группа, состоящая из порождающего элемента и всех его целых степеней. Конечна в случае, если порядок порождающего элемента конечен.

Ядро гомоморфизма — прообраз нейтрального элемента при гомоморфизме. Ядро всегда есть нормальная подгруппа, более того, любая нормальная подгруппа есть ядро некоторого гомоморфизма.

Литература

Полезное

Смотреть что такое «Порядок группы» в других словарях:

порядок группы — grupės eilė statusas T sritis fizika atitikmenys: angl. order of a group vok. Ordnung einer Gruppe, f rus. порядок группы, m pranc. ordre du groupe, m … Fizikos terminų žodynas

Порядок — в широком смысле слова гармоничное, ожидаемое, предсказуемое состояние или расположение чего либо, а также: порядок в физике расположение атомов, обладающее некоторой инвариантностью относительно сдвига; порядок в биологии один… … Википедия

Порядок (математика) — Порядок в широком смысле слова гармоничное, ожидаемое, предсказуемое состояние или расположение чего либо. Специализированные варианты использования слова: Порядок (физика) Порядок (биология) Математика Порядок величины количество цифр в числе. О … Википедия

Порядок элемента группы — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Порядок элемента — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

ПОРЯДОК — 1) П. алгебраич. кривой F( х, y)=0, где F( х, у) многочлен от хи у, наз. наивысшую степень членов этого многочлена. Напр., эллипс + =1 есть кривая второго П., а лемниската ( х 2+y2)2=а 2 ( х 2 у 2) кривая четвертого П. 2) П. бесконечно малой… … Математическая энциклопедия

Порядок Спорыньевые или Клавицепсовые (Саvicipitales) — Спорыньевые образуют перитеции в хорошо развитых стромах, состоящих только из гиф гриба. Стромы обычно мясистые, светло или яркоокрашенные, у некоторых представителей порядка темные. Их форма разнообразна, от распростертых но субстрату… … Биологическая энциклопедия

Порядок Циттариевые (Cyttariales) — Маленький порядок циттариевых объединяет дискомицеты, апотеции которых погружены в студенистые или мясистые стромы. Обычно считают, что сумки у представителей этой группы иноперкулятные, как у фацидиевых и гелоциевых (рис. 121), но у… … Биологическая энциклопедия

Порядок беннеттитовые (Bennettitales) — Беннеттитовые одна из наиболее известных групп голосеменных растений мезозойской эры. Они начали свое существование с триаса, а по некоторым данным с перми, т. е. с конца палеозойской эры. Расцвет группы приходился на середину мезозоя юру … Биологическая энциклопедия

Источник

Теорема Лагранжа утверждает, что для любой подгруппы H группы G порядок подгруппы делит порядок группы: | H | является делителем | G |. В частности, порядок | а | любого элемента является делителем | G |,

СОДЕРЖАНИЕ

Пример

•	е	s	т	ты	v	ш
е	е	s	т	ты	v	ш
s	s	е	v	ш	т	ты
т	т	ты	е	s	ш	v
ты	ты	т	ш	v	е	s
v	v	ш	s	е	ты	т
ш	ш	v	ты	т	s	е

Порядок и структура

2 + 2 + 2 знак равно 6 ≡ 0 ( мод 6 ) <\ Displaystyle 2 + 2 + 2 = 6 \ эквив 0 <\ pmod <6>>> .

Связь между двумя понятиями порядка следующая: если мы напишем

Для любого целого k имеем

Если a имеет бесконечный порядок, то все ненулевые степени a также имеют бесконечный порядок. Если a имеет конечный порядок, у нас есть следующая формула для порядка степеней a :

Подсчет по порядку элементов

Относительно гомоморфизмов

Уравнение класса

Важным результатом, касающимся заказов, является уравнение классов ; он связывает порядок конечной группы G с порядком ее центра Z ( G ) и размерами ее нетривиальных классов сопряженности :

Источник

Порядок группы г обозначается через ord (г) или | г |, а порядок элемента а обозначается через ord (а) или | а |, Порядок элемента а равен порядку его циклическая подгруппа ⟨а⟩ = <а k для k целое число>, подгруппа генерируется от а. Таким образом, | а | = | ⟨а⟩ |.

Теорема Лагранжа утверждает, что для любой подгруппы ЧАС из г, порядок подгруппы делит порядок группы: |ЧАС| это делитель из | G |. В частности, порядок |а| любого элемента является делителем |г|.

Содержание

пример

•	е	s	т	ты	v	ш
е	е	s	т	ты	v	ш
s	s	е	v	ш	т	ты
т	т	ты	е	s	ш	v
ты	ты	т	ш	v	е	s
v	v	ш	s	е	ты	т
ш	ш	v	ты	т	s	е

Порядок и структура

Порядок группы г а порядок его элементов дает много информации о структуре группы. Грубо говоря, чем сложнее факторизация из |г|, чем сложнее структура г.

2 + 2 + 2 = 6 ≡ 0 ( мод 6 ) < Displaystyle 2 + 2 + 2 = 6 эквив 0 < pmod <6>>> .

Связь между двумя понятиями порядка следующая: если мы напишем

Для любого целого числа k, у нас есть

а k = е тогда и только тогда, когда ord (а) разделяет k.

В общем, порядок любой подгруппы г делит порядок г. Точнее: если ЧАС является подгруппой г, тогда

ord (г) / ord (ЧАС) = [г : ЧАС], где [г : ЧАС] называется показатель из ЧАС в г, целое число. Это Теорема Лагранжа. (Это, однако, верно только тогда, когда G имеет конечный порядок. Если ord (г) = ∞, то частное ord (г) / ord (ЧАС) не имеет смысла.)

Следующее частичное обратное верно для конечные группы: если d делит порядок группы г и d это простое число, то существует элемент порядка d в г (это иногда называют Теорема Коши). Заявление не распространяется на составной заказы, например в Кляйн четыре группы не имеет элемента четвертого порядка). Это может быть показано индуктивное доказательство. [1] Следствия теоремы включают: порядок группы г это сила простого п тогда и только тогда, когда ord (а) это некоторая сила п для каждого а в г. [2]

Если а имеет бесконечный порядок, то все ненулевые степени а иметь бесконечный порядок. Если а имеет конечный порядок, мы имеем следующую формулу для порядка степеней а:

для каждого целого числа k. Особенно, а и его обратное а −1 в таком же порядке.

Подсчет по порядку элементов

Относительно гомоморфизмов

Групповые гомоморфизмы имеют тенденцию уменьшать порядок элементов: если ж: г → ЧАС является гомоморфизмом и а является элементом г конечного порядка, то ord (ж(а)) делит ord (а). Если ж является инъективный, затем ord (ж(а)) = ord (а). Это часто может быть использовано для доказательства отсутствия (инъективных) гомоморфизмов между двумя конкретно данными группами. (Например, не может быть нетривиального гомоморфизма час: S₃ → Z₅, потому что каждое число кроме нуля в Z₅ имеет порядок 5, который не делит порядки 1, 2 и 3 элементов в S₃.) Еще одно следствие: сопряженные элементы в таком же порядке.

Уравнение класса

Важным результатом о заказах является уравнение класса; он связывает порядок конечной группы г в порядке его центр Z (г) и размеры его нетривиальных классы сопряженности:

Источник

Порядок элемента группы

Если порядок элемента конечный — то наивным возведением в степень можно найти его порядок. Правда конечный — не значит маленький, так что может и не сработать на практике.

Если о группе что-то известно — часто можно дать эффективные ответы на оба Ваших вопроса. Скорее всего Ваши группы — именно такие: либо группы вычетов либо подгруппы симметрической группы малого порядка.

Почти наверное по сложению — иначе нулевым вопросом был бы порядок группы

Чтобы что-то показывать — нужно знать, что Вы знаете или не знаете и где у Вас камень преткновения образовался.

Разумеется, группа нециклическая. И максимальный порядок элемента в ней — 240.
Порядок группы — да, 480.

Вообще-то строение групп вычетов и то, когда они циклические — это неотъемлемая часть любого около-математического образования.

Тот, кто Вам это подсказал — жестоко ошибается. Либо Вы сами неправильно поняли подсказку — Вам могли сказать, что порядок группы — 480, а Вы это поняли как «максимальный порядок элемента».

Зато теперь у Вас есть хороший повод самостоятельно понять, почему прав Anonimus, а не неизвестный подсказчик. Как Вы при этом будете действовать — в конкретных терминах делимости или в абстрактных прямых суммах групп — вопрос вторичный и чисто технический. Я бы Вам посоветовал пока не усугублять с абстракцией.

Скорее всего по сложению — о чем я и сказал в №7.

Хотя, если специальность около-криптографическая — группа по умножению будет актуальнее.

А давать такие задачи вполне можно — они не требуют никаких знаний из теории групп и прекрасно решаются в рамках элементарной школьной математики. За одним исключением — доказать цикличность Zp без теории групп — очень сложно, с этим даже Эйлер не справился в свое время (но дело в том, что тут не надо доказывать цикличность, также можно и вовсе ее не использовать ).

Другой вопрос — зачем пускать изучение теории групп на самотек?

Только не начинайте обучение с поисковиков и википедии. Почитайте нормальные книжки. Винберг, например, или Кострикин. Первая более математизирована, вторая — более «народная», но на вкус и цвет. Ваши проблемы адекватно покроет любая.

Присоединяюсь к совету Anonimus Vulgaris ( не обращая внимание на понятные только мне его замечания о реинкарнации)- учиться не по интернету и Википедии, а по учебникам.
В ИКСИ используется учебник Кострикина и Глухова, Елизарова, Нечаева.
Я бы порекомндовал:
Математические и компьютерные основы криптологии. Учебное пособие

Авторы: Ю. С. Харин, В. И. Берник, Г. В. Матвеев, С. В. Агиевич

Харин Ю. С. Компьютерный практикум по математическим методам защиты информации: Учеб. пособие / Ю. С. Харин. С. В. Агиевич. — Мн.: БГУ, 2001. — 190 с.: ил.
ISBN 985-445-217-4
Данное учебное пособие является первым отечественным компьютерным практикумом по новому актуальному направлению прикладной ма тематики — математическим методам защиты информации. Содержит свыше 200 заданий по всем основным разделам криптологии, а также модели, методы и алгоритмы, необходимые для выполнения этих заданий в рамках лабораторных занятий на компьютере. Приводится описание оригинального пакета прикладных программ «КриптоЛаборатория». поддерживающего компьютерный практикум.
Для студентов бакалаврского и магистерского уровней, аспирантов, обучающихся: по математическим и инженерно-техническим специальностям, слушателей факультетов переподготовки и повышения квалификации, а также для специалистов в области прикладной математики, информатики и электроники, желающих познакомиться с математическими методами защиты информации.

Источник