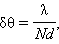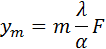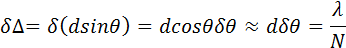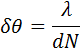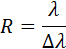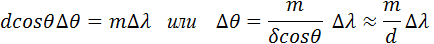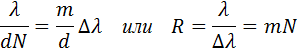Что такое порядок спектра
5.5. Дифракционная решетка
Широкое распространение в научном эксперименте и технике получили дифракционные решетки, которые представляют собой множество параллельных, расположенных на равных расстояниях одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционные решетки изготавливаются с помощью делительной машины, наносящей штрихи (царапины) на стекле или другом прозрачном материале. Там, где проведена царапина, материал становится непрозрачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.
Рассмотрим сначала дифракцию света от решетки на примере двух щелей. (При увеличении числа щелей дифракционные максимумы становятся лишь более узкими, более яркими и отчетливыми.)
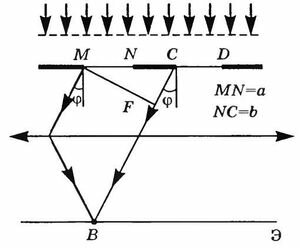
Пусть а — ширина щели, a b — ширина непрозрачного промежутка (рис. 5.6).
Рис. 5.6. Дифракция от двух щелей
Период дифракционной решетки — это расстояние между серединами соседних щелей:
Разность хода двух крайних лучей равна
Если разность хода равна нечетному числу полуволн
то свет, посылаемый двумя щелями, вследствие интерференции волн будет взаимно гаситься. Условие минимумов имеет вид
Эти минимумы называются дополнительными.
Если разность хода равна четному числу полуволн
то волны, посылаемые каждой щелью, будет взаимно усиливать друг друга. Условие интерференционных максимумов с учетом (5.36) имеет вид
Это формула для главных максимумов дифракционной решетки.
Кроме того, в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть главные минимумы решетки будут наблюдаться в направлениях, определяемых условием (5.21) для одной щели:
Если дифракционная решетка состоит из N щелей (современные решетки, применяемые в приборах для спектрального анализа, имеют до 200 000 штрихов, и период d = 0.8 мкм, то есть порядка 12 000 штрихов на 1 см), то условием главных минимумов является, как и в случае двух щелей, соотношение (5.41), условием главных максимумов — соотношение (5.40), а условие дополнительных минимумов имеет вид
Положение главных максимумов зависит от длины волны l. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный — наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Заметим, что в то время как спектральная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, наоборот, сильнее отклоняет красные лучи.
Важной характеристикой всякого спектрального прибора является разрешающая способность.
Разрешающая способность спектрального прибора — это безразмерная величина
Спектральные приборы. Дифракционная решетка
В состав видимого спектра света включены монохроматические волны с различными длинами. В излучении нагретых объектов (к примеру, нити лампы накаливания) длины волн беспрерывно заполняют весь диапазон видимого света. Данное излучение называют белым светом.
Свет, излучаемый, например, газоразрядными лампами или одним из множества других подобных им приборами, включает в свой состав отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн.
Комплекс монохроматических компонент в излучении называется спектром.
Белый свет имеет непрерывный спектр, излучение источников, в которых он испускается атомами вещества, и дискретный спектр.
Спектральные приборы – это устройства, с помощью которых изучаются спектры излучения источников.
Первый опыт по разложению белого света в спектр осуществил известный физик И. Ньютон в 1672 году.
Дифракционные решетки
В каждой точке P на экране в фокальной плоскости линзы сходятся лучи, который до линзы являлись параллельными между собой и расходились под некоторым углом θ к направлению падающей волны.
Интерференция волн
Колебание в точке P представляют собой следствие интерференции вторичных волн, которые сходятся в эту точку от разных щелей.
Для того, чтобы в точке P прослеживался интерференционный максимум, разность хода Δ между волнами, который испускают соседние щели, должна быть эквивалентной целому числу длин волн:
Где d – это период дифракционной решетки, а m – целое число, носящее название порядка дифракционного максимума. В точках экрана, для которых это условие выполнено, расположены главные максимумы дифракционной картины.
где F – фокусное расстояние.
Также следует обратить внимание на то, что в каждой точке фокальной плоскости линзы, имеет место интерференция N волн, которые приходят в эту точку от N щелей решетки. Данный феномен является так называемой многоволновой или же «многолучевой» интерференцией.
Распространение световой энергии в плоскости наблюдения значительно отличается от того, которое выходит в обыкновенных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, из-за чего амплитуда колебаний увеличивается в N раз, а интенсивность в N 2 раз, относительно колебания, которое провоцирует волна только от одной конкретной щели.
Здесь, дифракционные углы считаются достаточно малыми. Таким образом,
Где N d – это полный размер решетки. Данное выражение находится в полной симметрии с теорией дифракции в параллельных лучах. Согласно этой теории, дифракционная расходимость параллельного пучка лучей эквивалентна отношению длины волны λ к поперечному размеру препятствия.
Волновая природа света
Волновая природа света определяет разрешающую способность спектральных приборов, в частности, дифракционной решетки, так же от нее зависит предельное разрешение различных оптических инструментов, которые создают изображение объектов, таких как телескоп, микроскоп и др.
Из формулы решетки следует:
d d · cos θ · ∆ θ = m ∆ λ или ∆ θ = m δ cos θ ∆ λ ≈ m d ∆ λ
Что такое порядок спектра
Первый опыт по разложению белого света в спектр был осуществлен И. Ньютоном (1672 г.).
Простейшая дифракционная решетка состоит из прозрачных участков (щелей), разделенных непрозрачными промежутками. На решетку с помощью коллиматора направляется параллельный пучок исследуемого света. Наблюдение ведется в фокальной плоскости линзы, установленной за решеткой (рис. 3.10.3).
В каждой точке на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под определенным углом к направлению падающей волны. Колебание в точке является результатом интерференции вторичных волн, приходящих в эту точку от разных щелей. Для того, чтобы в точке наблюдался интерференционный максимум, разность хода между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн:
Следует обратить внимание на то, что в каждой точке фокальной плоскости линзы происходит интерференция волн, приходящих в эту точку от щелей решетки. Это так называемая многоволновая (или «многолучевая») интерференция. Распределение световой энергии в плоскости наблюдения резко отличается от того, которое получается в обычных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, потому амплитуда колебаний возрастает в раз, а интенсивность в раз по сравнению с колебанием, которое возбуждает волна только от одной щели.
Здесь для простоты полагается, что дифракционные углы достаточно малы. Следовательно,
|
где – полный размер решетки. Это соотношение находится в полном согласии с теорией дифракции в параллельных лучах, согласно которой дифракционная расходимость параллельного пучка лучей равна отношению длины волны к поперечному размеру препятствия.
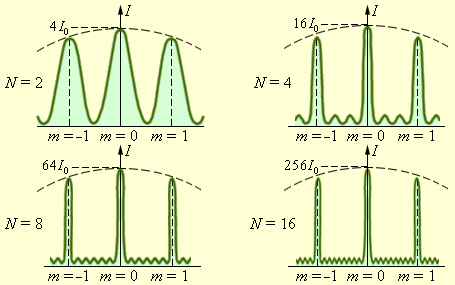
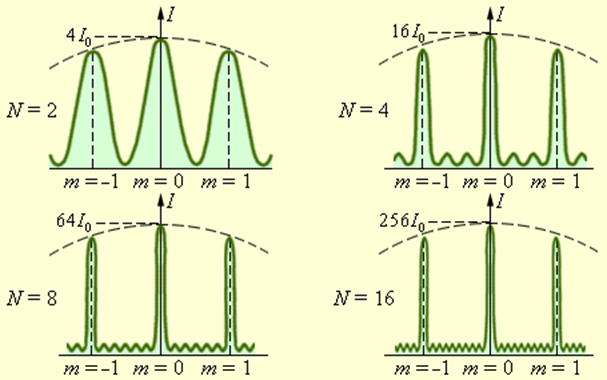
Можно сделать важный вывод: при дифракции света на решетке главные максимумы чрезвычайно узки. Рис. 3.10.5 дает представление о том, как меняется острота главных максимумов при увеличении числа щелей решетки.
Учебники
Журнал «Квант»
Общие
Дифракционная решетка. Дифракционный спектр
Важную роль в прикладной оптике играют явления дифракции на отверстиях в форме щели с параллельными краями. При этом использование дифракции света на одной щели в практических целях затруднено из-за слабой видимости дифракционной картины. Широко используются дифракционные решетки.
Дифракционная решетка — спектральный прибор, служащий для разложения света в спектр и измерения длины волны. Различают прозрачные и отражающие решетки. Дифракционная решетка представляет собой совокупность большого числа параллельных штрихов одинаковой формы, нанесенных на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга.
В прозрачной плоской дифракционной решетке (рис. 17.22) ширина прозрачного штриха равна а, ширина непрозрачного промежутка — Ь. Величина \(d = a + b = \frac<1>
Пусть плоская монохроматическая волна падает нормально к плоскости решетки (рис. 17.22). По принципу Гюйгенса—Френеля каждая щель является источником вторичных волн, способных интерферировать друг с другом. Получившуюся дифракционную картину можно наблюдать в фокальной плоскости линзы, на которую падает дифрагированный пучок.
Допустим, что свет дифрагирует на щелях под углом \(\varphi.\) Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного направления \(\varphi\) будут одинаковыми в пределах всей дифракционной решетки:
В тех направлениях, для которых разность хода равна четному числу полуволн, наблюдается интерференционный максимум. Наоборот, для тех направлений, где разность хода равна нечетному числу полуволн, наблюдается интерференционный минимум. Таким образом, в направлениях, для которых углы \(\varphi\) удовлетворяют условию
\(d \sin \varphi = m \lambda (m = 0,1,2, \ldots),\)
При наблюдении дифракции в немонохроматическом (белом) свете все главные максимумы, кроме нулевого центрального максимума, окрашены. Это объясняется тем, что, как видно из формулы \(\sin \varphi = \frac
Ширина спектра зависит от постоянной решетки и увеличивается при уменьшении d. Максимальный порядок спектра определяется из условия \(
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 517-518.
Спектральные приборы. Дифракционная решетка
В состав видимого света входят монохроматические волны с различными значениями длин. В излучении нагретых тел (нить лампы накаливания) длины волн непрерывно заполняют весь диапазон видимого света. Такое излучение называется белым светом. Свет, испускаемый, например, газоразрядными лампами и многими другими источниками, содержит в своем составе отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн. Совокупность монохроматических компонент в излучении называется спектром. Белый свет имеет непрерывный спектр, излучение источников, в которых свет испускается атомами вещества, имеет дискретный спектр. Приборы, с помощью которых исследуются спектры излучения источников, называются спектральными приборами.
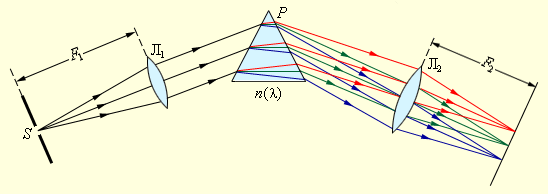
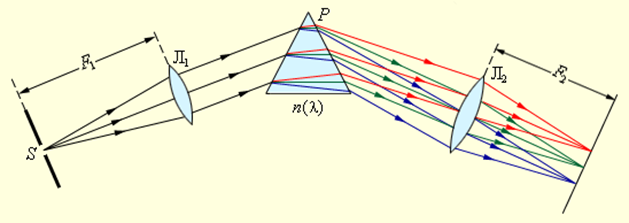
Для разложения излучения в спектр в простейшем спектральном приборе используется призма (рис. 3.10.1). Действие призмы основано на явлении дисперсии, то есть зависимости показателя преломления n вещества от длины волны света λ.
Разложение излучения в спектр при помощи призмы
Щель S, на которую падает исследуемое излучение, находится в фокальной плоскости линзы Л1. Эта часть прибора называется коллиматором. Выходящий из линзы параллельный пучок света падает на призму P. Вследствие дисперсии свет разных длин волн выходит из призмы под разными углами. В фокальной плоскости линзы Л2 располагается экран или фотопластинка, на которой фокусируется излучение. В результате в разных местах экрана возникает изображение входной щели S в свете разных длин волн. У всех прозрачных твердых веществ (стекло, кварц), из которых изготовляются призмы, показатель преломления n в диапазоне видимого света убывает с увеличением длины волны λ, поэтому призма наиболее сильно отклоняет от первоначального направления синие и фиолетовые лучи и наименее – красные. Монотонно убывающая зависимость n (λ) называется нормальной дисперсией.
Первый опыт по разложению белого света в спектр был осуществлен И.Ньютоном (1672 г.).
В спектральных приборах высокого класса вместо призм применяются дифракционные решетки. Решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки (рис. 3.10.2). У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50 – 100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки. В качестве дифракционной решетки может быть использован кусочек компакт-диска или даже осколок граммофонной пластинки.
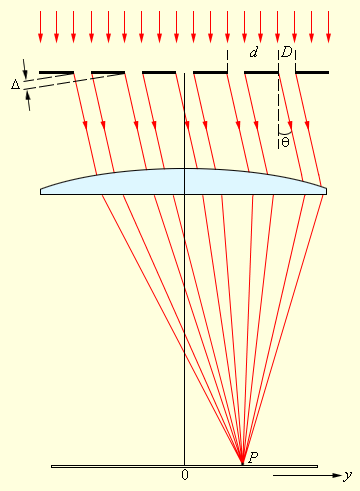
Простейшая дифракционная решетка состоит из прозрачных участков (щелей), разделенных непрозрачными промежутками. На решетку с помощью коллиматора направляется параллельный пучок исследуемого света. Наблюдение ведется в фокальной плоскости линзы, установленной за решеткой (рис. 3.10.3).
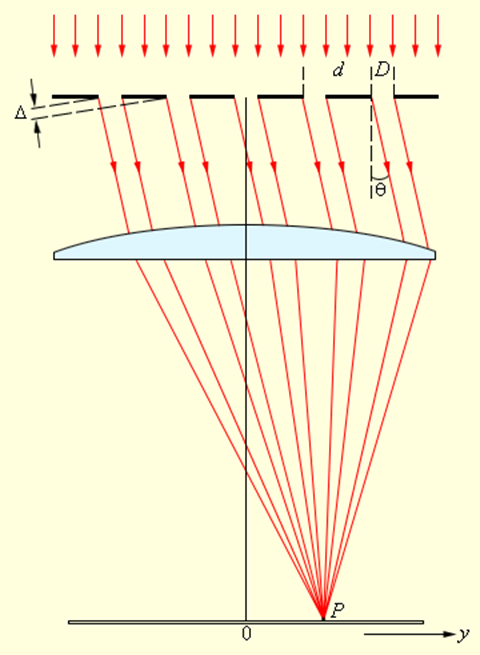
Дифракция света на решетке
В каждой точке P на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под определенным углом θ к направлению падающей волны. Колебание в точке P является результатом интерференции вторичных волн, приходящих в эту точку от разных щелей. Для того, чтобы в точке P наблюдался интерференционный максимум, разность хода Δ между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн:
Здесь d – период решетки, m – целое число, которое называется порядком дифракционного максимума. В тех точках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины.
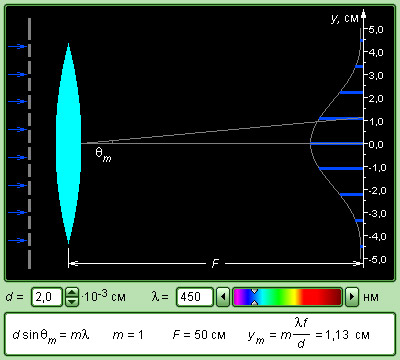
В фокальной плоскости линзы расстояние ym от максимума нулевого порядка (m = 0) до максимума m-го порядка при малых углах дифракции равно
где F – фокусное расстояние.
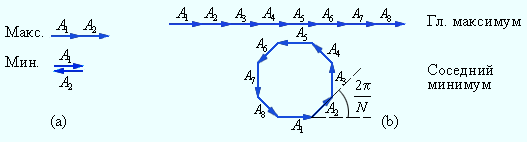
Следует обратить внимание на то, что в каждой точке фокальной плоскости линзы происходит интерференция N волн, приходящих в эту точку от N щелей решетки. Это так называемая многоволновая (или «многолучевая») интерференция. Распределение световой энергии в плоскости наблюдения резко отличается от того, которое получается в обычных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, потому амплитуда колебаний возрастает в N раз, а интенсивность в N 2 раз по сравнению с колебанием, которое возбуждает волна только от одной щели.
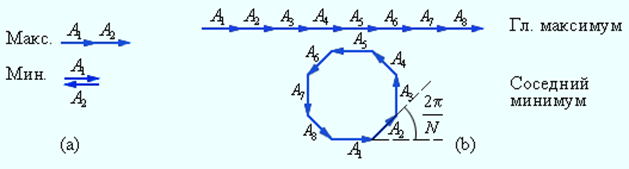
При смещении из главных максимумов интенсивность колебаний быстро спадает. Чтобы N волн погасили друг друга, разность фаз должна измениться на 2π / N, а не на π, как при интерференции двух волн. На рис. 3.10.4 изображена векторная диаграмма колебаний, возбуждаемых волнами от всех N щелей при условии, что сдвиг фаз волн от соседних щелей равен 2π / N, а соответствующая разность хода равна λ / N. Вектора, изображающие N колебаний, образуют в этом случае замкнутый многоугольник. Таким образом, при переходе из главного максимума в соседний минимум разность хода Δ = d sin θ должна измениться на λ / N. Из этого условия можно оценить угловую полуширину δθ главных максимумов:
Здесь для простоты полагается, что дифракционные углы достаточно малы. Следовательно,
где Nd – полный размер решетки. Это соотношение находится в полном согласии с теорией дифракции в параллельных лучах, согласно которой дифракционная расходимость параллельного пучка лучей равна отношению длины волны λ к поперечному размеру препятствия.
Сложение колебаний в максимуме и минимуме интерференционной картины: a – интерференция двух волн, b – интерференция N волн (N = 8)
Можно сделать важный вывод: при дифракции света на решетке главные максимумы чрезвычайно узки. Рис. 3.10.5 дает представление о том, как меняется острота главных максимумов при увеличении числа щелей решетки.
Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I0 – интенсивность колебаний при дифракции света на одной щели
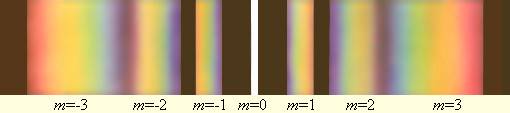
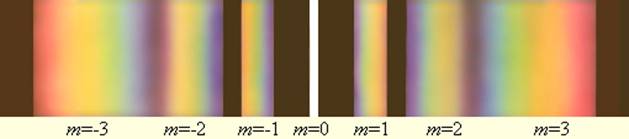
Как следует из формулы дифракционной решетки, положение главных максимумов (кроме нулевого) зависит от длины волны λ. Поэтому решетка способна разлагать излучение в спектр, то есть она является спектральным прибором. Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (т. е. при каждом значении m) возникает спектр исследуемого излучения, причем фиолетовая часть спектра располагается ближе к максимуму нулевого порядка. На рис. 3.10.6 изображены спектры различных порядков для белого света. Максимум нулевого порядка остается неокрашенным.
Разложение белого света в спектр с помощью дифракционной решетки
С помощью дифракционной решетки можно производить очень точные измерения длины волны. Если период d решетки известен, то определение длины сводится к измерению угла θm, соответствующего направлению на выбранную линию в спектре m-го порядка. На практике обычно используются спектры 1-го или 2-го порядков.
Если в спектре исследуемого излучения имеются две спектральные линии с длинами волн λ1 и λ2, то решетка в каждом спектральном порядке (кроме m = 0) может отделить одну волну от другой.
Одной из важнейших характеристик дифракционной решетки является ее разрешающая способность, характеризующая возможность разделения с помощью данной решетки двух близких спектральных линий с длинами волн λ и λ + Δλ. Спектральной разрешающей способностью R называется отношение длины волны λ к минимальному возможному значению Δλ, то есть
Разрешающая способность спектральных приборов, и, в частности, дифракционной решетки, также как и предельное разрешение оптических инструментов, создающих изображение объектов (телескоп, микроскоп) определяется волновой природой света. Принято считать, что две близкие линии в спектре m-го порядка различимы, если главный максимум для длины волны λ + Δλ отстоит от главного максимума для длины волны λ не менее, чем на полуширину главного максимума, т. е. на δθ = λ / Nd. По существу, это критерий Релея, примененный к спектральному прибору. Из формулы решетки следует:
где Δθ – угловое расстояние между двумя главными максимумами в спектре m-го порядка для двух близких спектральных линий с разницей длин волн Δλ. Для простоты здесь предполагается, что углы дифракции малы (cos θ ≈ 1). Приравнивая Δθ и δθ, получаем оценку разрешающей силы решетки:
Таким образом, предельное разрешение дифракционной решетки зависит только от порядка спектра m и от числа периодов решетки N.