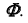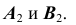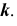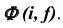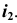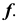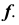Что такое постоянная монжа
Метод Монжа
Метод Монжа использует метод прямоугольных проекций или метод ортогонального проецирования геометрического образа (точки, прямой, плоскости, поверхности) на две взаимно перпендикулярные и взаимно связанные плоскости проекции лучами перпендикулярными этим плоскостям проекций, в этом состоит сущность метода Монжа:
H – горизонтальная плоскость проекции; V – фронтальная плоскость проекции; W – профильная плоскость проекции. Линии пересечения плоскостей проекции называются осью проекции или осью координат: ОХ = V ∩ H; ОУ = H ∩ W; ОZ= V ∩ W. А`– проекция точки А на плоскость H (горизонтальная проекция точки А); А»– проекция точки А на плоскость V (фронтальная проекция точки А); А»`– проекция точки А на плоскость W (профильная проекция точки А). Методы проецирования с использованием одно-картинных чертежей позволяют решать прямую задачу (т.е. по данному оригиналу построить его проекцию). Однако, обратную задачу (т.е. по проекции воспроизвести оригинал) решить однозначно невозможно. Эта задача допускает бесчисленное множество решений, т.к. каждую точку Аα плоскости проекций α можно считать проекцией любой точки проецирующего луча SАα, проходящего через Аα. Таким образом, рассмотренные одно-картинные чертежи не обладают свойством обратимости. Для получения обратимых одно-картинных чертежей их дополняют необходимыми данными. Существуют различные способы такого дополнения. Например, чертежи с числовыми отметками. Способ заключается в том, что наряду с проекцией точки А1 задаётся высота точки, т.е. её расстояние от плоскости проекций. Задают, также, масштаб. Такой способ используется в строительстве, архитектуре, геодезии и т. д. Однако, он не является универсальным для создания чертежей сложных пространственных форм.
В 1798 году французский геометр-инженер Гаспар Монж, обобщив накопленные к этому времени теоретические знания и опыт, впервые дал научное обоснование общего метода построения изображений, предложив рассматривать плоский чертёж, состоящий из двух проекций, как результат совмещения с плоскостью двух взаимно связанных взаимно перпендикулярных плоскостей проекций.
Отсюда ведёт начало принцип построения чертежей, получивший название Метод Монжа, которым мы пользуемся и поныне.
Научная электронная библиотека
Пиралова О. Ф., Ведякин Ф. Ф.,
1.6. Система трех плоскостей проекций. Эпюр Монжа
Эти координатные плоскости обозначаются:
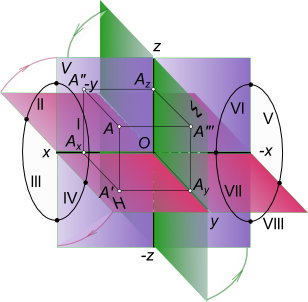
Линии пересечения этих плоскостей образуют координатные оси: ось абсцисс – Х; ось ординат – Y; ось аппликат – Z. Точка О пересечения координатных осей принимается за начало координат и обозначается буквой О. Положительными направлениями осей считают: для оси x − влево от начала координат, для оси Y − в сторону зрителя от плоскости π2, для оси z – вверх от плоскости π1; противоположные направления считают отрицательными.
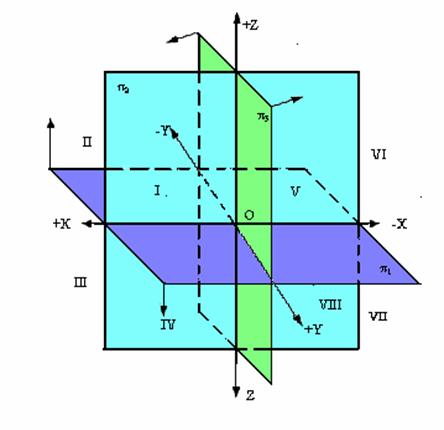
Рис. 1.12. Изображение системы трех плоскостей проекций
Для упрощения дальнейших рассуждений будем рассматривать только часть пространства, расположенную влево от профильной плоскости проекций π3.
При таком допущении три координатные плоскости проекций образуют четыре пространственных угла – октанта ( в общем случае – 8 октантов).
Оси ординат Y и аппликат Z делят профильную плоскость проекций π3 на четыре части:
Для того, чтобы получить плоскую (двухмерную) модель пространственных координатных плоскостей проекций, горизонтальную π1 и профильную π3 плоскости совмещают с фронтальной π2 в том порядке как это показано стрелками на рис. 1.12.
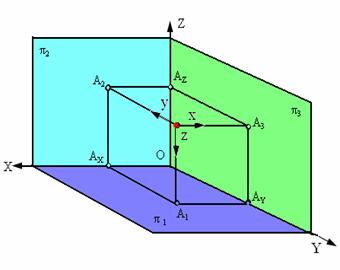
Рис. 1.13. Пространственная модель точки А
При этом горизонтальная плоскость проекций π1 вращается вокруг оси Х на 90°, а профильная плоскость проекций π3 вращается вокруг оси Z также на 90° (направление вращения показано на рис. 1.12).
Полученное таким образом совмещение трех плоскостей проекций (рис. 1.13) является плоской моделью системы трех пространственных координатных плоскостей
Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций π1, π2 и π3, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром Монжа.
Порядок построения эпюры точки, расположенной в первом октанте.
На рис. 1.13 изображена пространственная точка А, координаты которой (x, y, z) показывают величины расстояний, на которые точка удалена от плоскостей проекций.
Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций.
Точки пересечения этих перпендикуляров с плоскостями проекций образуют проекции точки А:
А1 – горизонтальную проекцию точки;
А2 – фронтальную проекцию точки;
А3 – профильную проекцию точки.
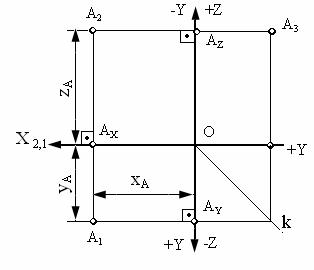
Рис. 1.14. Эпюр точки А
На рис. 1.14 плоскости проекций π1 и π3 совмещены с плоскостью чертежа ( с плоскостью проекции π2), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А1, А2, А3) и таким образом получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А – ее эпюра.
Положение проекций точки А на эпюре однозначно определяется ее тремя координатами (рис. 1.14).
На рис. 1.13 и рис. 1.14 также видно, что на эпюре горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси Х, а также фронтальная и профильная проекции – на одном перпендикуляре к оси Z:
А1А2 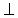
Из рис 1.12 видно, что точки, расположенные в различных октантах, имеют определенные знаки координат.
В таблице приведены знаки координат точек, расположенных в различных октантах
Моделирование поверхностей на эпюре Монжа с примерами
Содержание:
Моделирование поверхностей на эпюре Монжа:
В начертательной геометрии при моделировании поверхностей преимущественно используют кинематический и каркасный способы их образования.
При кинематическом способе поверхность рассматривается как совокупность всех последовательных положений некоторой линии — образующей, перемещающейся в пространстве по определенному закону. Линия, которую пересекают все образующие поверхности, называется направляющей.
Упорядоченное множество линий, принадлежащих поверхности, называется ее каркасом. Обычно в качестве линий каркаса используют семейство образующих или семейство направляющих.
При каркасном способе поверхность рассматривается как совокупность некоторого числа линий, образующих каркас. Основное отличие каркасных поверхностей от кинематических состоит в том, что для первых задается определенное число линий каркаса — дискретный каркас, а у вторых в любой точке поверхности может быть построена линия каркаса, т. е. поверхность имеет непрерывный каркас.
При моделировании поверхности важную роль играет ее определитель.
Определитель поверхности
Совокупность условий, задающих поверхность, называется определителем поверхности. Определитель состоит из двух частей: геометрической и алгоритмической.
Геометрическая часть определителя включает в себя геометрические элементы, участвующие в образовании поверхности. Такой набор элементов называется репером (от французского слова repere — метка, ориентир).
Алгоритмическая часть определителя содержит перечень операций, позволяющих реализовать переход от репера к остальным точкам поверхности.
При моделировании поверхности необходимо:
На эпюре Монжа поверхность задается проекциями ее репера.
Построение произвольной точки, принадлежащей поверхности, осуществляется с помощью простейших линий каркаса поверхности, проходящих через эту точку.
При моделировании поверхности возникает понятие очерка поверхности.
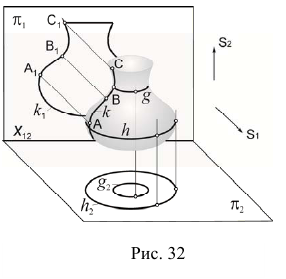
Очерк поверхности
Совокупность точек касания проецирующих прямых поверхности образует контурную линию k (рис. 32). Очерк k1 — проекция контурной линии на плоскость проекций. Контурная линия делит поверхность на две части — видимую и невидимую.
При моделировании поверхности по методу Монжа различают фронтальный
Моделирование линейчатых поверхностей
Линейчатая поверхность образуется движением прямой линии (образующей), которая в общем случае пересекает три направляющие, в частном случае — две или одну направляющую.
Линейчатые поверхности с одной направляющей
Линейчатые поверхности с одной направляющей образуются движением прямой линии, которая пересекает направляющую (кривую или ломаную линию) и вершину (собственную или несобственную точку). В табл. 1 представлены различные формы поверхности с одной направляющей в зависимости от вида направляющей и вершины.
Моделирование конической поверхности
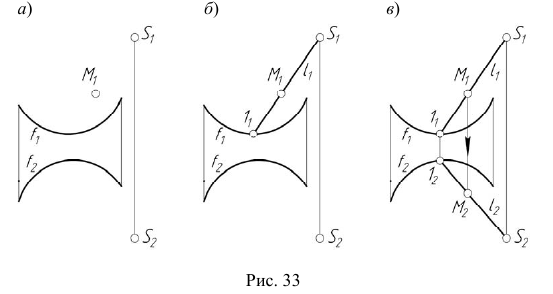
Для построения модели конической поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей (кривая линия) и вершины (собственная точка), а также решить задачу построения произвольной точки поверхности.
Задача 1.
На эпюре Монжа построить произвольную точку M, принадлежащую конической поверхности 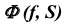
Алгоритм решения
6. Через точку 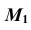
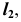
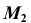
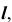
Моделирование цилиндрической поверхности
Для построения модели цилиндрической поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей 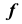
Моделирование пирамидальной поверхности
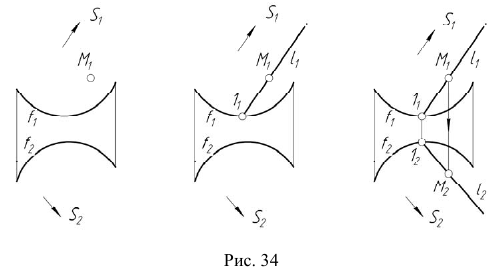
Для построения модели пирамидальной поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей 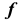
Моделирование призматической поверхности
Для построения модели призматической поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей 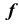
Пример:
Построение линии 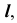
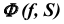
Порядок построения
1. Построение очерковых линий и определение видимости направляющей 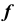
Для определения видимости линии 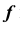
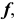
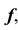
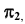
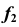
2. Определение проекций точек изменения видимости линии 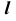
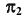
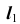
Построение начинается с горизонтальной проекции — с точек касания 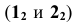
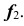
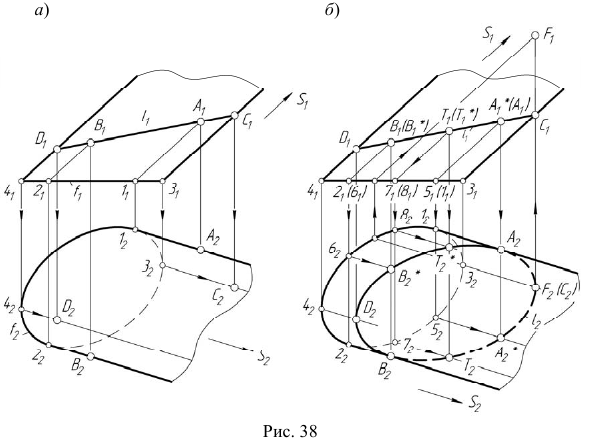
3. Построение точек С и D (рис. 38, а). Построение начинается с фронтальных проекций 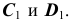
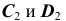
4. Построение проекций точек 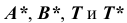
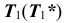
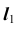
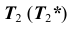
Аналогично строятся остальные точки заданной линии.
5. Определение видимости линии 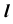
Видимость линии 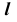
Линейчатые поверхности с двумя направляющими и плоскостью параллелизма
Такие поверхности образуются движением прямой, которая движется параллельно некоторой плоскости 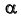
В табл. 2 представлены различные формы поверхности с двумя направляющими в зависимости от вида направляющих.
Наибольшее применение из приведенных (см. Табл. 2) поверхностей в инженерной практике нашла косая плоскость. Косую плоскость также называют гиперболическим параболоидом, так как ее каркас состоит не только из прямых линий, но также из семейств кривых второго порядка — гипербол и парабол.
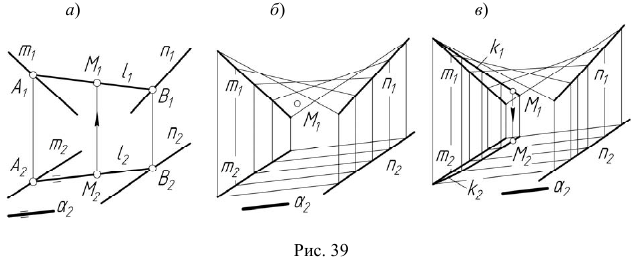
Моделирование косой плоскости
Для построения модели косой плоскости необходимо задать на эпюре Монжа проекции направляющих m и n, а также проекции плоскости параллелизма 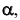
Задача 2.
На эпюре Монжа построить недостающую проекцию 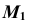
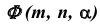
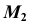
Плоскостью параллелизма в данной задаче является горизонтально-проецирующая плоскость 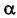
Алгоритм решения
На рис. 39, б, в показано построение недостающей проекции 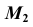
Проекция 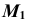
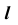
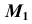
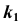
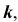
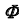
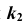
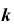
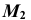
Линейчатые проецирующие поверхности
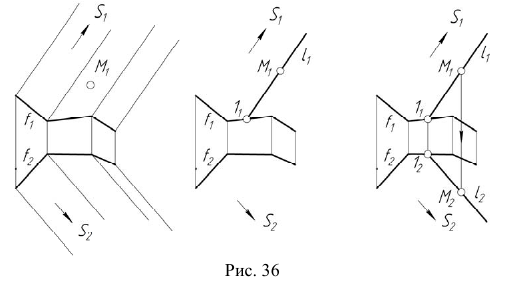
Цилиндрическая и призматическая поверхности могут занимать проецирующее положение в том случае, если направление на вершину (несобственную точку) будет совпадать с направлением проецирования на одну из плоскостей проекций. Другими словами, образующие проецирующей поверхности будут перпендикулярны одной из плоскостей проекций.
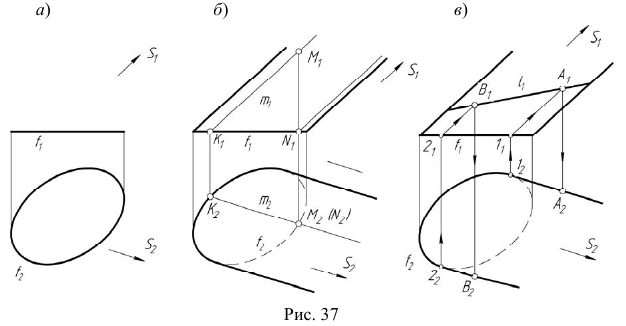
На рис. 40 приведен пример фронтально-проецирующей цилиндрической поверхности.
Фронтальная проекция любой точки, принадлежащей поверхности 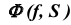
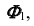
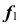
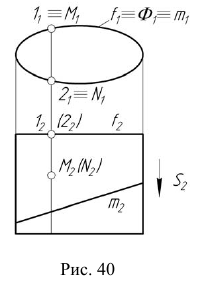
На рис. 40 также показано положение проекций точек M, N и линии m, принадлежащих цилиндрической поверхности. На рис. 41 приведен пример горизонтально-проецирующей призматической поверхности.
Горизонтальная проекция любой точки, принадлежащей поверхности 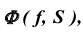
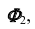
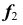
На рис. 41 также показано положение проекций точек M, N и линии m, принадлежащих призматической поверхности.
Моделирование поверхностей вращения
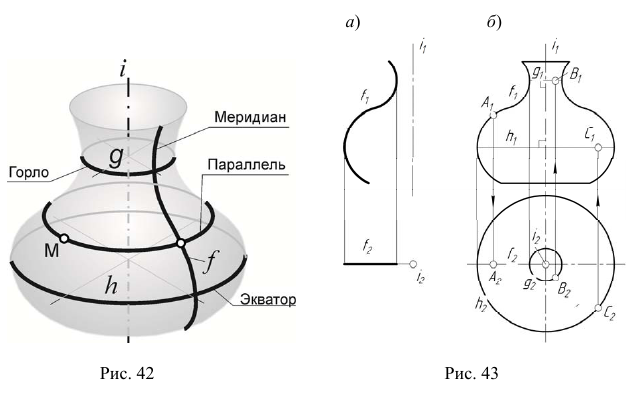
Поверхность вращения образуется вращением какой-либо линии (образующей) вокруг неподвижной оси (рис. 42). Как правило, ось вращения располагается перпендикулярно одной из плоскостей проекций.
Если образующая поверхности вращения — прямая линия, то образуется линейчатая поверхность. Если образующая — кривая, поверхность вращения будет относиться к классу нелинейчатых поверхностей.
Репер поверхности вращения включает в себя ось вращения i и образующую линию f. Каждая точка образующей линии вращается по окружности, которая называется параллелью. Плоскость этой параллели перпендикулярна оси вращения, а центр принадлежит оси вращения.
Параллель наибольшего радиуса называется экватором, а параллель наименьшего радиуса — горлом.
Меридиан — линия на поверхности, расположенная в одной плоскости с осью вращения. Главный меридиан — меридиан, плоскость которого параллельна плоскости проекций. Если ось вращения перпендикулярна плоскости 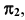
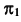
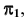
Один из очерков поверхности вращения определяется главным меридианом, а второй — экватором или экватором и горлом.
Моделирование поверхности вращения общего вида
Для построения модели поверхности вращения необходимо задать на эпюре Монжа проекции ее репера: оси вращения 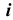
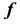
Задача 3.
На эпюре Монжа построить произвольную точку 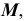
Алгоритм решения 1
Алгоритм решения 2
1. Отмечаем произвольно проекцию 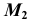
2. Через 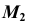
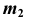
3. Находим проекцию 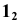
4. Строим проекции 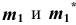
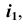
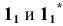
5. Через точку 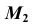
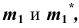
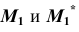
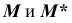
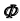
Приведенные алгоритмы решения подобной задачи применимы для любой поверхности вращения.
В зависимости от формы образующей линии 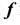
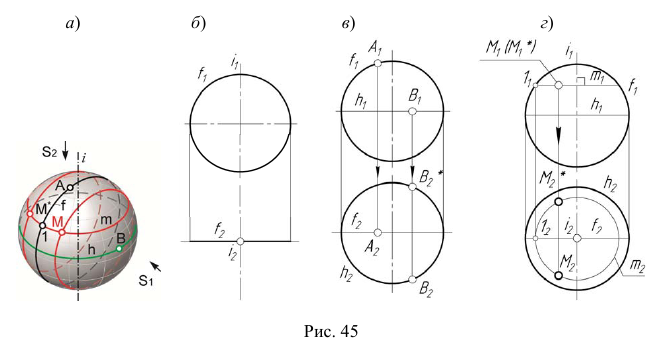
Моделирование сферы
Сфера образуется вращением окружности вокруг одного из ее диаметров (рис. 45, а). Один из реперов сферы — ось вращения 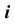
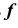
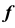
На рис. 45, г показано построение точки M, принадлежащей сфере 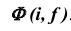
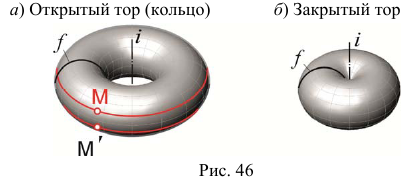
Моделирование торовой поверхности
Торовая поверхность образуется вращением окружности вокруг оси, которая расположена в плоскости окружности, но не проходит через ее центр (рис. 46).
Репером торовой поверхности будут ось вращения 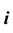
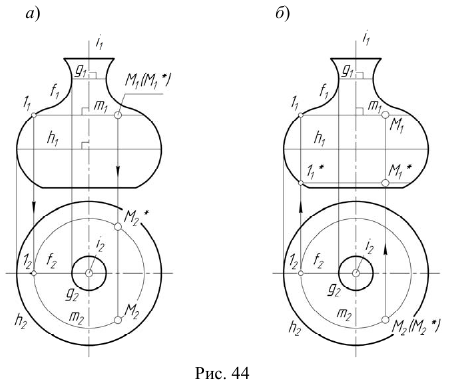
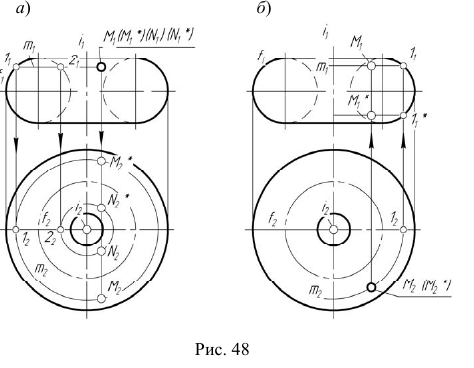
На рис. 47 изображены три модели торовой поверхности в зависимости от взаимного положения оси вращения и образующей окружности, а также модели точек, принадлежащих контурным линиям торовой поверхности. Если ось вращения 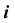
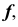
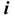
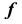
На рис. 48, а показано построение произвольной точки M, принадлежащей торовой поверхности 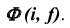
Линейчатые поверхности вращения
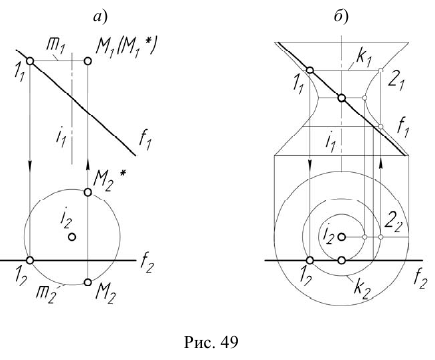
При вращении прямой линии, которая пересекает ось вращения в собственной или несобственной точке, образуются, соответственно, коническая или цилиндрическая поверхности. Если прямая линия 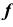
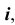
Эта поверхность также может быть получена путем вращения гиперболы вокруг ее мнимой оси. На рис. 49, а показано построение произвольной точки M, принадлежащей поверхности однополостного гиперболоида вращения 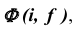
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.