Что такое посылка в логике
Посылка (логика)
Аристотель утверждал, что любой логический аргумент может быть сведен к двум посылкам и выводу. Посылки иногда опускают, в этом случае они называются опущенными посылками, например:
Сократ смертен, так как все люди смертны.
Очевидно, что Сократ является человеком (эта посылка опущена). Развернутым суждением было бы:
Так как все люди смертны, а Сократ — человек, то следовательно Сократ смертен.
В этом примере два первых независимых высказывания — «все люди смертны» и «Сократ — человек» — это посылки, в то время как «Сократ смертен» является выводом.
Доказательство вывода зависит как от истинности обеих посылок, так и от обоснованности аргумента.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Деду́кция (лат. deductio — выведение, также дедуктивное умозаключение, силлогизм) — метод мышления, следствием которого является логический вывод, в котором частное заключение выводится из общего. Цепь умозаключений (рассуждений), где звенья (высказывания) связаны между собой логическими выводами.
На эту страницу установлено перенаправление со страницы «A posteriori», см. также статью о музыкальном альбоме «A Posteriori».Апостерио́ри, а постерио́ри (лат. a posteriori букв. «из последующего») — знание, полученное из опыта. Противопоставляется априори — доопытному знанию. Значение термина исторически менялось: нынешнее значение установилось благодаря И. Канту и его работе «Критика чистого разума» (впервые опубликована в 1781 году, второе издание в 1787 г.) Однако, в латинской форме, выражения.
Инду́кция (лат. inductio — наведение, от лат. inducere — влечь за собой, установить) — процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не строго через законы логики, а скорее через некоторые фактические, психологические или математические представления.Объективным основанием индуктивного умозаключения является всеобщая связь явлений в природе.
10. Краткий курс логики. Умозаключение
Умозаключение – это форма мышления, в которой из двух суждений, называемых посылками, вытекает третье – вывод.
1. Посылка: «Все люди – смертны».
2. Посылка: «Сократ – человек»
Ввод: «Сократ – смертный».
Умозаключения бывают непосредственные и опосредованные. Непосредственные умозаключения делаются из одной посылки, и являют собой уже известные нам действия над суждениями (обращения, превращения, противоставления предикату), а так же преобразование суждений по логическому квадрату. Опосредованные умозаключения делаются из нескольких посылок, о них мы и будем говорить в данной главе.
Существуют такие виды опосредованных умозаключений, их еще называют методами мышления:
Дедуктивный метод (Силлогизм) – метод при котором вывод о частном делается из общей совокупности вещей, о которых говориться в посылках. Проще говоря – вывод от общего к частному. К примеру:
1 посылка: «В группе 311 все студенты отличники».
2 посылка: «Этот ученик из 311 группы»
Вывод: «Этот ученик – отличник».
Еще пример:
1 посылка: «В этом ящике все шарики красные»
2 посылка: «Этот шарик их этого ящика»
Вывод: «Этот шарик красный».
Преимущество дедуктивного метода заключается в том, что при правильном использовании всегда дает точные выводы. Важно понимать, что все посылки входящие в силлогизм должны быть истинными, ложность хотя бы одной из них, ведет к ложности вывода. В принципе кто знаком с произведениями Артура Конана Дойля, должен был слышать о дедуктивном способе мышления. Его использовал Шерлок Холмс, в одном из произведений он приводит пример своего дедуктивного умозаключения Ватсону. Около жертвы преступления было найдена выкуренная сигарета, все решили, что сигарету выкурил полковник перед смертью. Однако у покойного были большие пышные усы, а сигарета была докуренная полностью. Шерлок Холм берется доказывать, что полковник не мог курить эту сигарету, так как он непременно бы подпалил бы себе усы. Вывод дедуктивный и верный, так как из общего правила вытекает частное.
Общее правило и первая посылка, выглядит так: «Все люди, которые носят большие, пышные усы не могут выкурить сигарету до конца»
Событие или вторая посылка выглядит так: «Полковник носил большие, пышные усы».
Вывод: «Полковник не мог выкурить сигарету до конца»
Индукция – метод, при котором вывод об общем делается из совокупности частных случаев. Проще говоря – это вывод от частного к общему. И пример тому:
1 посылка: «Первый, второй и третий студент – отличники».
2 посылка: «Эти студенты из 311 группы».
Вывод: «Все студенты в 311 группе – отличники».
1 посылка: ««Этот шарик красный».
2 посылка: «Этот шарик их этого ящика».
Вывод: «В этом ящике все шарики красные»
Некоторые учебники различают полную и не полную индукцию, полная индукция это когда перечисляются все элементы конечного множества вещей, о котором рассуждают. В нашем примере берутся все ученики и проверяют отличники они все или нет, а уже потом заключают обо всей группе. Не полная или частичная индукция – это наши примеры, в которых берутся только некоторые элементы конечного множества вещей. Само собой разумеется, не полное индуктивное заключения, на отмену от дедуктивного носит вероятностный, а не достоверный характер. Тем не менее, это не мешает пользоваться этим методом умозаключения в повседневной жизни. К примеру, мы, я уверен, слышали такое высказывание из уст женщины «Все мужчины – козлы», а ведь вывод об общем сделан из частного, по всем правилам индуктивного мышления.
1 посылка: «Первый человек – козел»
2 посылка: «Второй человек – козел».
3 посылка: «Эти люди – мужчины»
Вывод: «Все мужчины – козлы».
Чаще всего не полные индуктивные выводы – неверные. Их преимущество состоит в том, что они направленны на расширения знаний о предмете, могут указать на новые их свойства, в то время как индуктивный метод чаще всего направлен на выяснения уже известных фактов.
Я с некоторыми другими логиками выделяю еще такой вид умозаключения как Абдукция. Абдукция – это вид умозаключения, при котором на основе общего, делается вывод о причине частного, проще говоря – это вывод от общего к причине частного.
Я считаю, на отмену от общепринятого мнения, что именно этот вид умозаключений использовал на самом деле Шерлок Холмс, а так же другие реальные и не реальные детективы.
Чтобы понять, в чем заключается суть Абдукции, ее лучше рассматривать в сравнении с другими видами умозаключения.
А: «В этом ящике все шарики красные»
Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
Как видим с помощью дедукции – мы узнали результат, теперь переделаем рассуждения под индукцию:
Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
А: «В этом ящике все шарики красные»
Индукция, вывод от частного к общему открыл нам правило. Не трудно догадаться, что должен быть еще один вид умозаключений, который открывал бы нам случай, причину, ним и является Абдукция. Такой вид умозаключений будет выглядит так:
Существует, еще такой вид умозаключений как «вывод по аналогии». Это когда на основе свойств, признаков одного предмета делается вывод о свойствах другого. Формально это выглядит так:
Предмет А имеет свойство а, б, с, д.
Предмет В имеет свойсво а, б, с.
Вероятно В имеет и свойство д.
Так же как и неполная индукция умозаключения по аналогии носит вероятностный характер, но, не смотря на это, он широко используется, как в повседневной жизни, так и в науке.
Вернемся к дедукции. Мы предположили, что дедуктивный вид умозаключения имеет достоверный характер. Но, тем не менее, надо выделить некоторые правила простого силлогизм, чтобы это было действительно так. Итак, рассмотрим общие правила силлогизма.
1. В силлогизме должно быть только три термина или не должно быть термина, который употребляется в двух значениях. Если такой есть считается, что в силлогизме больше трех терминов, так как четвертый подразумевается. К примеру:
Движение – вечно.
Хождение в университет – это движение.
Хождение в университет – вечно.
Термин «Движение» употреблено в двух смыслах, в первом суждении, первой посылке оно обозначает всеобщее мировое изменения. А во второй механическое передвижение из одной точки в другую.
2. Средний термин должен быть распределён хотя бы в одной из посылок. Средний термин – это термин, который является базисом рассуждения и находиться в каждой из посылок.
Все хищные животные (+) – живые существа (-)
Все хомяки (+) – живые существа (-).
Все хомяки – хищные животные.
Средним термином является «живые существа». В обоих посылках его объем не распределён. В первой посылке оно не распределено, потому, что живые существа – это не только хищные животные. А во втором, потому, что живые существа – это не только все хомяки. Соответственно вывод в данном суждении не верный.
Еще один пример, который недавно прочел в одном журнале:
Все старые фильмы (+) – черно белые (-)
Все пингвины (+) – черно белые (-).
Пингвины – это старые фильмы.
Средний термин, то есть термин, который встречается в двух посылках – «черно белый». Как в первом, так и во втором суждении он не распределён, ведь черно белыми могут быть не только все старые фильмы или все пингвины.
4. Посылки силлогизма не могут быть только отрицательными. Вывод в таком силлогизме в лучшем случае будет вероятностным, но чаще всего его либо вообще невозможно сделать, либо он ложен.
5.Посылки силлогизма не могут быть только частными. Хотя бы одна посылка из силлогизма должна быть общая. В силлогизме, в котором две посылки частные сделать вывод не возможно.
6.Если в силлогизме одна посылка отрицательная, то и вывод будет отрицательным.
7.Если в силлогизме одна посылка частная, вывод из него следует так же только частный.
Силлогизм – самый распространённый вид умозаключений, потому, мы часто используем его в повседневной жизни и науке. Однако мы редко соблюдаем его логическую форму, и пользуемся сокращенными силлогизмами. К примеру: «Сократ смертный, потому, что все люди смертные». «Этот шарик красный, потому, что его взяли из ящика, в котором все шарики красные». «Железо – электропроводно, так как все металлы электропроводны» и т.д.
Различают такие виды сокращенного силлогизма:
Энтимема – это сокращенный силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что из простого силлогизма можно вывести три энтимемы. К примеру, из простого силлогизма:
Все металлы – электропроводные.
Железо – это метал.
Железо – электропроводно.
Можно вывести три энтимемы:
1. «Железо – электропроводно так как оно является металлом». (пропущена первая посылка)
2. «Железо – электропроводно потому, что все металлы электропроводны». (пропущена вторая посылка)
3. «Все металлы электропроводны, а железо тоже метал». (пропущен вывод)
Следующий вид сокращенного умозаключения – Эпихейрема. Оно являет собой простой силлогизм, в которой две посылки – энтимемы.
Сначала сделаем из двух силлогизмов энтимемы:
Силлогизм №1.
Все то, что ограничивает человеческую свободу, делает его рабом.
Социальная необходимость ограничивает человеческую свободу
Социальная необходимость делает человека рабом.
Первая энтимема, если пропустить первую посылку будет выгладить так:
«Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Силлогизм №2.
Все действия, которые дают возможность существовать в социуме – являются социальной необходимостью.
Работа – это действие, которое дает возможность существовать в социуме.
Работа – это социальная необходимость.
Вторая энтимема, если пропустить первую посылку: «Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме».
Теперь сделаем силлогизм из двух энтимем, который и будет нашей эпихейремой:
Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме.
Работа – делает человека рабом.
Не исключено, что именно в таком порядке рассуждал Ницше говоря: «Мы видим, к чему сводится жизнь в обществе — каждый отдельный индивид приносится в жертву и служит орудием. Пройдите по улице, и вы увидите только «рабов». Куда? Зачем?»
Сорит – полисиллогизм, в котором пропущено суждение, связывающее два простых силлогизма, то есть вывод первого силлогизма, который стал первой посылкой второго, попросту упускается.
Все что развивает память и мышления – полезно.
Изучения наук – развивает память и мышления.
Логика – это наука.
Изучения логики – полезно.
Как видим суть силлогизма от того, что оно из полисиллогизма превратилось в сорит, не поменялась.
Простой категорический силлогизм



От греческого syllogismos – сосчитывание.
Новое знание, получаемого с помощью простого категорического силлогизма высчитывается из имеющегося суждения.
А простой категорический называется, так как в состав суждения входят простые категорические суждения.
Простой категорический силлогизм (ПКС) – это дедуктивное умозаключение об отношении двух крайних терминов на основании их отношения к среднему термину.
Состав ПКС: Состоит из двух посылок и заключения.
Например:
Значит все логики смертные.
Над чертой 2 посылки, а потом заключение.
В свою очередь, посылки и заключение состоят из 3 терминов. Эти термины называются «термины ПКС»:
Р – больший термин – это предикат заключения силлогизма. В нашем случае – это «смертны». Посылка, которая содержит больший термин – большая посылка.
В ясной логической форме ПКС большая посылка записывается вверху, меньшая под большей, а заключение под чертой.
М – средний термин – это термин, который содержится в обоих посылах, но отсутствует в заключении. В нашем случае – это «люди».
Аксиома силлогизма:
Имеет две трактовки:
1) Атрибутивная: Признак признака некоторой вещи есть признак самой той вещи; то, что противоречит признаку вещи, противоречит и вещи (признак признака есть признак вещи).
2) Объемная: Все, что утверждается (или отрицается) относительно всех предметов класса, утверждается (или отрицается) относительно каждого предмета и любой части предметов этого класса (сказанное обо всем и ни об одном).
Атрибутивная трактовка нашего примера говорит, что признак людей есть «смертны». А признак «люди» признака «смертны» есть признак «логики» вещи «смертны».
Общие правила ПКС:
Всего 7 правил, которые поделены на 2 группы.
I группа – правила терминов:
2) Средний термин должен быть распределен хотя бы в одной из посылок. Таблица распределенности:
| Распределенность | S | P |
| A | + | — |
| I | — | — |
| E | + | + |
| O | — | + |
Например, «Все печеночные сосальщики поедают печень. Некоторые люди в ресторане тоже поедают печень. Значит некоторые люди в ресторане – печеночные сосальщики.» Средний термин – «поедают печень». Меньший термин «люди в ресторане». А больший термин – «печеночные сосальщики». То есть получилось, что средний термин в обоих случаях с минусом. Это неправильно.
3) Если крайний термин (больший или меньший) не распределен в посылке, то он не должен быть распределен в заключении. Ошибка: «незаконное расширение термина». Например, «Я – человек (А). Ты не я (Е). Значит, ты не человек (Е)». Находим термины силлогизма: Средний термин – «Я». Меньший термин – «Ты». Больший термин – «Человек». Этот силлогизм неправильный.
II группа – правила посылок:
1) Должна быть хотя бы одна общая посылка (из двух частных вывод не делается). То есть одна из посылок должна быть общим суждением.
2) Должна быть хотя бы одна утвердительная посылка (из двух отрицательных посылок вывод не делается).
4) Если одна из посылок отрицательная, то и вывод в силлогизме отрицательный.
Решение задач по ПКС:
3 вида задач:
1) Проверка ПКС на правильность.
Задача:
«Каждый пассионарий может изменить ход истории. Ни один дворник не является пассионарием. Значит, ни один дворник не может изменить ход истории».
Определить термины и расставить распределенность.
Решение:
Определить термины:
P – тот, кто может изменить ход истории.
Расставляем распределенность:
Е Ни один S+ не есть M+
Е Ни один S+ не есть Р+
Проверить на правильность (по правилам): Первое – не нарушается. Второе – не нарушается. Третье – нарушается. То есть ПКС неправильный.
Задача:
«Все студенты бюджетники ИЮ, являются студентами 111 группы. Некоторые студенты 111 группы посещают консультации. Значит, некоторые студенты бюджетники ИЮ посещают консультации».
1) Ищем заключение силлогизма и термины: «Значит, некоторые студенты бюджетники ИЮ посещают консультации»
S – студент бюджетник ИЮ.
P – студент, который посещает лекции.
M – студент 111 группы.
2) Составляем схему:
I Некоторые М- есть Р-.
I Некоторые S- есть Р-.
3) Проверяем нарушаемость правил:
1) Нарушается. Остальное можно не проверять.
Задача:
«Все гуси серы. Гусь Гриша не серый. Значит, гусь Гриша не гусь».
1) Ищем заключение и термины: «Значит, гусь Гриша не гусь».
Силлогизм неправильный, так как нарушается аксиома силлогизма.
2) Выведение заключения из посылок.
Задача:
«Все ананасы приятны на вкус. Картошка не ананас. Значит…»
Раз нет заключения, то мы не можем определить меньший и больший термины. Ошибка заключается в том, что студенты пытаются определить термины.
Поэтому надо начать решение этой задачи с поиска среднего термина.
1) Средний термин: M – ананас.
2) Условно обозначаем крайние термины, из которых получим заключение:
А – вещи приятные на вкус.
3) Пишем структуру силлогизмов:
О Некоторые S- не есть Р+
Устанавливаем распределенность терминов.
Порядок выведения из посылок заключения:
1) Определить связку в заключении. Связка определяется по правилам и аксиомам посылок. Вывод в нашем суждении тоже отрицателен. Если одна из посылок отрицательна, то вывод отрицателен.
2) Определить вид суждения в заключении. Вид суждения в заключении определяется по распределенности крайних терминов. Крайние термины А и В. У них распределенность – и +. Когда выводим вывод нельзя нарушать 3 правило посылки. Поэтому, мы не можем взять в качестве вывода общеотрицательное суждение, потому что там оба термина распределены.
3) Снести крайние термины заключения. Делаем по распределенности терминов. В О S-, а Р+, следовательно, подставляем: А-=S-, а B+=Р+
Меняем термины суждения на наши термины.
Записываем вывод: «Некоторые вещи, приятные на вкус, не являются картошкой».
Задача:
«Все зелюки являются момзюками. Каждый снарк является зелюком. Значит…».
Что такое посылка в логике
1. хНПЪБЛМАЮЕОЙЕ: ПРТЕДЕМЕОЙЕ, УФТХЛФХТБ, ЛМБУУЙЖЙЛБГЙС.
йУФЙООПУФШ Й РТБЧЙМШОПУФШ НЩУМЙ.
уФТХЛФХТБ ХНПЪБЛМАЮЕОЙС
фТБДЙГЙПООЩК ДТЕЧОЕЗТЕЮЕУЛЙК УЙММПЗЙЪН:
2. рлу: ПРТЕДЕМЕОЙЕ, УФТХЛФХТБ, ПВЭЙЕ РТБЧЙМБ.
бЛУЙПНБ УЙММПЗЙЪНБ
пВЭЙЕ РТБЧЙМБ рлу.
I. рТБЧЙМБ ФЕТНЙОПЧ:
1) Ч УЙММПЗЙЪНЕ ДПМЦОП ВЩФШ ФПМШЛП 3 ФЕТНЙОБ
фЕТНЙО н ДПМЦЕО ВЩФШ ПДОЙН Й ФЕН ЦЕ РПОСФЙЕН Ч ПВЕЙИ РПУЩМЛБИ, ЙОБЮЕ РПМХЮЙН ПЫЙВЛХ, ОБЪЩЧБЕНХА «ХЮЕФЧЕТЕОЙЕН ФЕТНЙОПЧ».
2) УТЕДОЙК ФЕТНЙО ДПМЦЕО ВЩФШ ТБУРТЕДЕМЕО ИПФС ВЩ Ч ПДОПК ЙЪ РПУЩМПЛ.
еУМЙ УТЕДОЙК ФЕТНЙО ОЕ ТБУРТЕДЕМЕО ОЙ Ч ПДОПК ЙЪ РПУЩМПЛ, ФП ПФОПЫЕОЙЕ НЕЦДХ ЛТБКОЙНЙ ФЕТНЙОБНЙ Ч ЪБЛМАЮЕОЙЙ ПУФБЕФУС ОЕПРТЕДЕМЕООЩН.
3) ФЕТНЙО, ОЕ ТБУРТЕДЕМЕООЩК Ч РПУЩМЛБИ, ОЕ НПЦЕФ ВЩФШ ТБУРТЕДЕМЕО Ч ЪБЛМАЮЕОЙЙ.
рТЙ ОБТХЫЕОЙЙ ЬФПЗП РТБЧЙМБ ЧПЪОЙЛБЕФ МПЗ. ПЫЙВЛБ «ОЕЪБЛПООПЕ ТБУЫЙТЕОЙЕ ФЕТНЙОБ».
чУЕ РЕДБЗПЗЙ ЧПУРЙФБООЩ
пО ОЕ РЕДБЗПЗ
пО ОЕЧПУРЙФБО
II. рТБЧЙМБ РПУЩМПЛ:
1) йЪ ДЧХИ ПФТЙГБФЕМШОЩИ РПУЩМПЛ ЪБЛМАЮЕОЙЕ УДЕМБФШ ОЕМШЪС (ИПФС ВЩ ПДОБ ЙЪ РПУЩМПЛ ДПМЦОБ ВЩФШ ХФЧЕТДЙФЕМШОПК).
оЙ ПДЙО УФХДЕОФ ОЕ СЧМСЕФУС РТЕРПДБЧБФЕМЕН
CФХДЕОФ йЧБОПЧ ОЕ СЧМСЕФУС РТЕРПДБЧБФЕМЕН
?
2) йЪ ДЧХИ ЮБУФОЩИ РПУЩМПЛ ЪБЛМАЮЕОЙЕ ОЕ УМЕДХЕФ (ИПФС ВЩ ПДОБ ЙЪ РПУЩМПЛ ДПМЦОБ ВЩФШ ПВЭЙН УХЦДЕОЙЕН).
йЪ ДЧХИ ЮБУФОЩИ РПУЩМПЛ РТБЧЙМШОПЕ ЪБЛМАЮЕОЙЕ УДЕМБФШ ОЕЧПЪНПЦОП.
рТЙНЕТ РТБЧ. ЧЩЧПДБ:
оЙ ПДЙО РБРПТПФОЙЛ ОЙЛПЗДБ ОЕ ГЧЕФЕФ
ьФП ТБУФЕОЙЕ ГЧЕФЕФ
ьФП ТБУФЕОЙЕ ОЕ РБРПТПФОЙЛ
4) ЕУМЙ ПДОБ ЙЪ РПУЩМПЛ ЮБУФОБС, ФП Й ЪБЛМАЮЕОЙЕ ДПМЦОП ВЩФШ ЮБУФОЩН.
3. жЙЗХТЩ Й НПДХУЩ РТПУФПЗП ЛБФЕЗПТЙЮЕУЛПЗП УЙММПЗЙЪНБ
I ЖЙЗХТБ
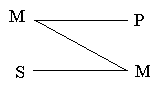
ч 1-К ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП УХВЯЕЛФБ Ч ВПМШЫЕК РПУЩМЛЕ РТЕДЙЛБФБ Ч НЕОШЫЕК.
рТЙНЕТ:
рТБЧЙМБ 1-К ЖЙЗХТЩ:
1) ВoМШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ПВЭЕК (б ЙМЙ е);
2) НeОШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ХФЧЕТДЙФЕМШОПК (б ЙМЙ I).
II ЖЙЗХТБ
чП 2-К ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП РТЕДЙЛБФБ Ч ПВЕЙИ РПУЩМЛБИ
ьФПФ УНЕТФЕМШОЩК ХДБТ (т) ОБОЕУЕО ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ (M)
пВЧЙОСЕНЩК (S) ОЕ СЧМСЕФУС ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ (н)
пВЧЙОСЕНЩК (S) ОЕ ОБОЕУ ЬФПФ УНЕТФЕМШОЩК ХДБТ (P)
рТБЧЙМБ 2-К ЖЙЗХТЩ:
1) ВoМШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ПВЭЙН УХЦДЕОЙЕН (б, е);
2) ПДОБ ЙЪ РПУЩМПЛ ДПМЦОБ ВЩФШ ПФТЙГБФЕМШОЩН УХЦДЕОЙЕН (E, I).
чУЕ ЖЙЪЙЛЙ УФТЕНСФУС Л ЙУФЙОЕ
оЕЛПФПТЩЕ ЙУФПТЙЛЙ УФТЕНСФУС Л ЙУФЙОЕ
оЕЛПФПТЩЕ ЙУФПТЙЛЙ СЧМСАФУС ЖЙЪЙЛБНЙ — ОЕЧЕТОП, Ф. Л. ПВЕ РПУЩМЛЙ ХФЧЕТДЙФЕМШОЩЕ УХЦДЕОЙС
оЕЛПФПТЩЕ МАДЙ НПЗХФ ВЩФШ ПФГБНЙ
оЙ ПДОБ ЦЕОЭЙОБ ОЕ НПЦЕФ ВЩФШ ПФГПН
оЕЛПФПТЩЕ ЦЕОЭЙОЩ ОЕ НПЗХФ ВЩФШ МАДШНЙ — ОЕЧЕТОП, Ф. Л. ВoМШЫБС РПУЩМЛБ ЮБУФОПЕ УХЦДЕОЙЕ
III ЖЙЗХТБ
ч 3-ЕК ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП УХВЯЕЛФБ Ч ПВЕЙИ РПУЩМЛБИ.
оЙ ПДЙО УФТБХУ (н) ОЕ МЕФБЕФ (т)
чУЕ УФТБХУЩ (н) РФЙГЩ (S)
оЕЛПФПТЩЕ РФЙГЩ (S) ОЕ МЕФБАФ (P)
рТБЧЙМБ 3-К ЖЙЗХТЩ:
1) НeОШЫБС РПУЩМЛБ ДПМЦОБ ВЩФШ ХФЧЕТДЙФЕМШОЩН УХЦДЕОЙЕН (б, I);
2) ЪБЛМАЮЕОЙЕ ДПМЦОП ВЩФШ ЮБУФОЩН УХЦДЕОЙЕН (I, п).
чУЕ УФХДЕОФЩ СЧМСАФУС МАДШНЙ
оЕЛПФПТЩЕ УФХДЕОФЩ ОЕ СЧМСАФУС НХЦЮЙОБНЙ
оЕЛПФПТЩЕ НХЦЮЙОЩ ОЕ СЧМСАФУС МАДШНЙ — ОЕЧЕТОП, Ф. Л. НЕОШЫБС РПУЩМЛБ ПФТЙГБФЕМШОБС
чУЕ УФХДЕОФЩ СЧМСАФУС МАДШНЙ
чУЕ УФХДЕОФЩ СЧМСАФУС ЦЙЧЩНЙ УХЭЕУФЧБНЙ
чУЕ ЦЙЧЩЕ УХЭЕУФЧБ СЧМСАФУС УФХДЕОФБНЙ — ОЕЧЕТОП, Ф. Л. ЪБЛМАЮЕОЙЕН СЧМСЕФУС ПВЭЕЕ УХЦДЕОЙЕ.
IV ЖЙЗХТБ
ч 4-К ЖЙЗХТЕ УТЕДОЙК ФЕТНЙО ЪБОЙНБЕФ НЕУФП РТЕДЙЛБФБ Ч ВПМШЫЕК Й УХВЯЕЛФБ Ч НЕОШЫЕК РПУЩМЛЕ.
оЙ ПДЙО УЮБУФМЙЧЩК ЮЕМПЧЕЛ(т) ОЕ УФТЕНЙФУСЛ УРТБЧЕДМЙЧПУФЙ (н)
оЕЛПФПТЩЕ УФТЕНСЭЙЕУС Л УРТБЧЕДМЙЧПУФЙ МАДЙ (M) СЧМСАФУС АТЙУФБНЙ (S)
оЕЛПФПТЩЕ АТЙУФЩ ОЕУЮБУФОЩ
рЕТЧБС ЖЙЗХТБ ФТБДЙГЙПООП УЮЙФБЕФУС Ч МПЗЙЛЕ ПУОПЧОПК. юЕФЧЕТФБС ЖЙЗХТБ ОПУЙФ ЙУЛХУУФЧЕООЩК ИБТБЛФЕТ, ЙУРПМШЪХЕФУС ТЕДЛП Й, ЛБЛ РТБЧЙМП, РТЕПВТБЪХЕФУС Ч ДТХЗЙЕ.
ъБДБЮЙ, ТЕЫБЕНЩ РТЙ РПНПЭЙ УЙММПЗЙЪНПЧ:
пРТПЧЕТЦЕОЙЕ ОЕРТБЧЙМШОЩИ ДЕДХЛГЙК ЙМЙ ОЕРТБЧЙМШОЩИ РПДЮЙОЕОЙК.
дБООБС ЪБДБЮБ РТПФЙЧПРПМПЦОБ 1-К Й УЙММПЗЙЪНЩ ЕЕ ТЕЫБАЭЙЕ ЮБУФП ЙУРПМШЪХАФУС ДМС ПРТПЧЕТЦЕОЙС ОЕРТБЧЙМШОЩИ ЧЩЧПДПЧ, УДЕМБООЩИ РП 1-К ЖЙЗХТЕ.
ьФХ ЪБДБЮХ ТЕЫБАФ УЙММПЗЙЪНБНЙ РП 2-К ЖЙЗХТЕ (оБРТ: ьФПФ УНЕТФ. ХДБТ ОБОЕУЕО ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ. пВЧЙОСЕНЩК ОЕ СЧМСЕФУС ЮЕМПЧЕЛПН ПЗТПНОПК УЙМЩ. ъОБЮЙФ, ПВЧЙОСЕНЩК ОЕ ОБОЕУ ЬФПФ УНЕТФЕМШОЩК ХДБТ).
пВПУОПЧБОЙЕ ЙУЛМАЮЕОЙК ЙЪ ПВЭЙИ РПМПЦЕОЙК.
ьФБ УЙФХБГЙС ЮБУФП ЧУФТЕЮБЕФУС Ч УРПТЕ. рТЕДРПМПЦЙН, ЧБЫ ПРРПОЕОФ ЧЩДЧЙЗБЕФ ЛБЛПЕ-МЙВП ПВЭЕЕ РПМПЦЕОЙЕ, Б ЧБН ОБДП ДПЛБЪБФШ ЙУЛМАЮЕОЙЕ ЙЪ ОЕЗП. фПЗДБ НПЦОП УНЕМП РТЙВЕЗОХФШ Л 3-ЕК ЖЙЗХТЕ (оБРТ: рТЕДРПМПЦЙН, ОБН ОБДП ДПЛБЪБФШ, ЮФП УХЦДЕОЙЕ «ЧУЕ МАДЙ ЙНЕАФ РТЕУФХРОЩЕ УЛМПООПУФЙ» ОЕ СЧМСЕФУС ЙУФЙООЩН. фПЗДБ ОБН ОБДП РПУФТПЙФШ УЙММПЗЙЪН РП 3-ЕК ЖЙЗХТЕ: оЙ ПДЙО ТЕВЕОПЛ ОЕ ЙНЕЕФ РТЕУФХРОЩИ ОБЛМПООПУФЕК. лБЦДЩК ТЕВЕОПЛ СЧМСЕФУС ЮЕМПЧЕЛПН. уМЕДПЧБФЕМШОП, ОЕЛПФПТЩЕ МАДЙ ОЕ ЙНЕАФ РТЕУФХРОЩИ ОБЛМПООПУФЕК)
лТПНЕ ФПЗП, Ч ЛБЦДПК ЖЙЗХТЕ ЧЩДЕМСАФ НПДХУЩ.
| жЙЗ. I | жЙЗ. II | жЙЗ. III | жЙЗ. IV |
| AAA (Barbara) | EAE (Cesare) | AAI (Darapti) | AAI (Bramantip) |
| EAE (Celarent) | AEE (Camestres) | IAI (Disamis) | AEE (Camenes) |
| AII (Darii) | EIO (Festino) | AII (Datisi) | IAI (Dimaris) |
| EIO (Ferio) | AOO (Baroco) | EAO (Felapton) | EAO (Fesapo) |
| OAO (Bocardo) | EIO (Fresison) | ||
| EIO (Ferison) |
иПД ТБУУХЦДЕОЙС РП 4-К ЖЙЗХТЕ ОЕ ФЙРЙЮЕО ДМС РТПГЕУУБ НЩЫМЕОЙС (4-С ЖЙЗХТБ СЧМСЕФУС ЙУЛХУУФЧЕООПК) РТБЧЙМБ ЬФПК ЖЙЗХТЩ ОБНЙ ОЕ ТБУУНБФТЙЧБАФУС
тБЪОПЧЙДОПУФЙ РТПУФПЗП ЛБФЕЗПТЙЮЕУЛПЗП УЙММПЗЙЪНБ:
йЪ ЬФПЗП УЙММПЗЙЪНБ НПЦОП РПУФТПЙФШ УМЕДХАЭЙЕ ЬОФЙНЕНЩ:
у ПРХЭЕООПК ВoМШЫЕК РПУЩМЛПК: «лХТЕОЙЕ ЪБУМХЦЙЧБЕФ ОБЛБЪБОЙС, РПФПНХ ЮФП ПОП РПТПЛ»
у ПРХЭЕООПК НЕОШЫЕК РПУЩМЛПК: «чУСЛЙК РПТПЛ ЪБУМХЦЙЧБЕФ ОБЛБЪБОЙС, РПЬФПНХ ЛХТЕОЙЕ ЪБУМХЦЙЧБЕФ ОБЛБЪБОЙС:
ьОФЙНЕНБ ЮБУФП ЙУРПМШЪХЕФУС Ч РПЧУЕДОЕЧОПН НЩЫМЕОЙЙ Й Ч ПТБФПТУЛПК РТБЛФЙЛЕ. уПЛТБЭЕООБС ЖПТНБ УРПУПВУФЧХЕФ МХЮЫЕНХ ЧПУРТЙСФЙА. лТПНЕ ФПЗП РТЙ РПНПЭЙ ЬОФЙНЕНЩ ДПУФЙЗБЕФУС ЬЖЖЕЛФ ХВЕДЙФЕМШОПУФЙ, ФБЛ ЛБЛ УПВЕУЕДОЙЛ ЧЩОХЦДЕО ТЕЛПОУФТХЙТПЧБФШ ЕЕ ДП РПМОПЗП ХНПЪБЛМАЮЕОЙС Й ОБЮЙОБЕФ УЮЙФБФШ ЪБЛМАЮЕОЙЕ УЧПЙН УПВУФЧЕООЩН.
тБЪМЙЮБАФ РТПЗТЕУУЙЧОЩК Й ТЕЗТЕУУЙЧОЩК РПМЙУЙММПЗЙЪН.
Б) рТПЗТЕУУЙЧОЩН РПМЙУЙММПЗЙЪНПН ОБЪЩЧБЕФУС РПМЙУЙММПЗЙЪН, Ч ЛПФПТПН ЪБЛМАЮЕОЙЕ РТПУЙММПЗЙЪНБ УФБОПЧЙФУС ВoМШЫЕК РПУЩМЛПК ЬРЙУЙММПЗЙЪНБ.
у РПНПЭША ЬФПЗП РТПЗТЕУУЙЧОПЗП РПМЙУЙММПЗЙЪНБ НЩ РПЬФБРОП У НБЛУЙНБМШОПК ПЮЕЧЙДОПУФША РЕТЕОЕУМЙ РТЙЪОБЛ «УНЕТФОЩК» У ПВЭЕЗП РПОСФЙС «ЦЙЧПЕ УХЭЕУФЧП» ОБ ЕДЙОЙЮОПЕ РПОСФЙЕ «уПЛТБФ»
В) тЕЗТЕУУЙЧОЩН РПМЙУЙММПЗЙЪНПН ОБЪЩЧБЕФУС РПМЙУЙММПЗЙЪН, Ч ЛПФПТПН ЪБЛМАЮЕОЙЕ РТПУЙММПЗЙЪНБ УФБОПЧЙФУС НЕОШЫЕК РПУЩМЛПК ЬРЙУЙММПЗЙЪНБ.
чУЕ НЩУМСЭЙЕ МАДЙ УРПУПВОЩ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ СЧМСАФУС НЩУМСЭЙНЙ МАДШНЙ
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ УРПУПВОЩ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА
чУЕ МАДЙ, УРПУПВОЩЕ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА, ЪБУМХЦЙЧБАФ УОЙУИПЦДЕОЙС
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ УРПУПВОЩ Л УБНПУПЧЕТЫЕОУФЧПЧБОЙА
оЕЛПФПТЩЕ РТЕУФХРОЙЛЙ ЪБУМХЦЙЧБАФ УОЙУИПЦДЕОЙС
ч РТПЗТЕУУЙЧОПН УПТЙФЕ РТПРХЭЕОЩ ВoМШЫЙЕ РПУЩМЛЙ ЬРЙУЙММПЗЙЪНПЧ:
дБООБС ЬРЙИЕКТЕНБ УПУФПЙФ ЙЪ ДЧХИ ЬОФЙНЕН У РТПРХЭЕООЩНЙ ВoМШЫЙНЙ РПУЩМЛБНЙ.
4. чЩЧПДЩ ЙЪ УМПЦОЩИ УХЦДЕОЙК.
рТБЧЙМП ХУМПЧОПЗП УЙММПЗЙЪНБ: УМЕДУФЧЙЕ УМЕДУФЧЙС ЕУФШ УМЕДУФЧЙЕ ПУОПЧБОЙС ;
х ЬФПЗП УЙММПЗЙЪНБ ЧПЪНПЦОЩ 4 НПДХУБ:
| рПОЕОУ | фПММЕОУ | ||
| p→q | p→q | p→q | p→q |
| p | q | ¬p | ¬q |
| q | p | ¬q | ¬p |
дПУФПЧЕТОЩЕ НПДХУЩ
нПДХУ РПОЕОУ (ТБУУХЦДЕОЙЕ ЙДЕФ ПФ ХФЧЕТЦДЕОЙС ПУОПЧБОЙС Л ХФЧЕТЦДЕОЙА УМЕДУФЧЙС):
| p→q | еУМЙ Ч ЙНРЕТЙСИ ОБЮЙОБЕФ ТХЫЙФШУС УЕНШС, ФП ПОЙ ПВТБЭБАФУС Ч РТБИ. |
| p | ч тЙНУЛПК ЙНРЕТЙЙ ОБЮБМБ ТХЫЙФШУС УЕНШС. |
| q | пОБ ПВТБФЙМБУШ Ч РТБИ. |
нПДХУ ФПММЕОУ (ТБУУХЦДЕОЙЕ ЙДЕФ ПФ ПФТЙГБОЙС УМЕДУФЧЙС Л ПФТЙГБОЙА ПУОПЧБОЙС):
| p→q | еУМЙ РПДЗПФПЧМАУШ, ФП УДБН ЬЛЪБНЕО. |
| ¬q | ьЛЪБНЕО С ОЕ УДБМ |
| ¬p | с ОЕ РПДЗПФПЧЙМУС. |
рТБЧДПРПДПВОЩЕ (ОЕРТБЧЙМШОЩЕ НПДХУЩ):
дБООЩЕ НПДХУЩ ОЕ РПЪЧПМСАФ ХУФБОПЧЙФШ ЗМБЧОХА РТЙЮЙОХ УМЕДУФЧЙС Й РПЬФПНХ ДБАФ МЙЫШ РТБЧДПРПДПВОЩЕ ЪБЛМАЮЕОЙС.
(1) ХФЧЕТЦДБАЭЕ-ПФТЙГБАЭЙК (modus ponendo tollens)
| pvq | мЙВП РБО, МЙВП РТПРБМ. |
| p | рБО. |
| ¬q | оЕ РТПРБМ. |
(2) ПФТЙГБАЭЕ-ХФЧЕТЦДБАЭЙК (modus tollendo ponens)
| pvq | мЙВП РБО, МЙВП РТПРБМ. |
| ¬p | оЕ РБО |
| q | рТПРБМ. |
рТБЧЙМБ:
1) Ч ДЙЪЯАОЛФЙЧОЩИ РПУЩМЛБИ ДПМЦОЩ ВЩФШ РЕТЕЮЙУМЕОЩ ЧУЕ ЮМЕОЩ ДЙЪЯАОЛГЙЙ (ДЕМЕОЙС);
2) ЮМЕОЩ ДЕМЕОЙС ДПМЦОЩ ЙУЛМАЮБФШ ДТХЗ ДТХЗБ (УФТПЗБС ДЙЪЯАОЛГЙС).
5. йОДХЛФЙЧОЩЕ ХНПЪБЛМАЮЕОЙС Й БОБМПЗЙЙ.
ч ПУОПЧЕ ТБУУХЦДЕОЙС РП БОБМПЗЙЙ МЕЦЙФ УИПДУФЧП НЕЦДХ РТЕДНЕФБНЙ. уФЕРЕОШ ДПУФПЧЕТОПУФЙ ФБЛПЗП ЧЩЧПДБ ЪБЧЙУЙФ ЛБЛ ПФ ЮЙУМБ УИПДОЩИ РТЙЪОБЛПЧ (ЮЕН ВПМШЫЕ, ФЕН МХЮЫЕ), ФБЛ Й ПФ ЙИ УХЭЕУФЧЕООПУФЙ (ЮЕН УХЭЕУФЧЕООЕЕ РТЙЪОБЛ, ФЕН ЧЕТПСФОЕЕ РТБЧЙМШОЩК ЧЩЧПД).