Что такое поверхность в геометрии

Поверхность

Полезное

Смотреть что такое «Поверхность» в других словарях:

ПОВЕРХНОСТЬ — ПОВЕРХНОСТЬ, поверхности, жен. Наружная, особенно верхняя сторона предмета. Поверхность земли. Поверхность воды. Гладкая, зеркальная поверхность. || Граница, отделяющая геометрическое тело от внешнего пространства или от другого тела; след… … Толковый словарь Ушакова

ПОВЕРХНОСТЬ — ПОВЕРХНОСТЬ, поверхности, жен. Наружная, особенно верхняя сторона предмета. Поверхность земли. Поверхность воды. Гладкая, зеркальная поверхность. || Граница, отделяющая геометрическое тело от внешнего пространства или от другого тела; след… … Толковый словарь Ушакова

поверхность — См … Словарь синонимов

ПОВЕРХНОСТЬ — ПОВЕРХНОСТЬ, математическое понятие, возникшее как абстракция понятия деформированного куска плоскости. Поверхность обычно бывает границей двух смежных областей пространства. Поверхности могут быть гладкими (сфера, цилиндр), многогранными, с… … Современная энциклопедия

поверхность — ПОВЕРХНОСТЬ, гладь, зеркало … Словарь-тезаурус синонимов русской речи

Поверхность — ПОВЕРХНОСТЬ, математическое понятие, возникшее как абстракция понятия деформированного куска плоскости. Поверхность обычно бывает границей двух смежных областей пространства. Поверхности могут быть гладкими (сфера, цилиндр), многогранными, с… … Иллюстрированный энциклопедический словарь

ПОВЕРХНОСТЬ — общая часть двух смежных областей пространства. В аналитической геометрии в пространстве поверхности выражаются уравнениями, связывающими координаты их точек, напр. Ax + By + Cz + D = 0 уравнение плоскости, x2 + y2 + z2 = R2 уравнение сферы … Большой Энциклопедический словарь

ПОВЕРХНОСТЬ — ПОВЕРХНОСТЬ, и, жен. 1. В математике: общая часть геометрических тел. 2. Наружная сторона чего н. П. озера. Скользить по поверхности чего н. (также перен.: не вникать глубоко в суть, ограничиваясь лишь приблизительным, внешним знакомством).… … Толковый словарь Ожегова

ПОВЕРХНОСТЬ — граница разделамежду двумя контактирующими средами. В разл. ситуациях употребляются такжетермины: свободная, или атом но чистая, П. (П. твёрдого тела в вакууме … Физическая энциклопедия

Поверхность — (Surface, Oberflache). Всякую непрерывную кривую линиюможно представить, как след движущейся точки. подобно этому и всякую П.можно образовать или описать движением в пространстве некоторой кривойлинии неизменяемого или изменяемого вида и размеров … Энциклопедия Брокгауза и Ефрона

Поверхность — уровня. Если равнодействующая сил, приложенных кматериальной точке, имеет П. функцию V, то все пространство, в которомможет находиться точка, можно представить себе заполненным системоюбесконечного множества поверхностей, на каждой из которых V… … Энциклопедия Брокгауза и Ефрона

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

7.1. Понятия и определения

В начертательной геометрии фигуры задаются графически, поэтому целесообразно рассматривать поверхность как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии. Образование поверхности с помощью линии позволяет дать иное определение поверхности, базирующейся на таких основных элементарных геометрических понятиях, как точка и множество. В свою очередь, линия определяется как непрерывное однопараметрическое множество точек, поэтому можно дать следующее определение поверхности:

Поверхностью называется непрерывное двупараметрическое множество точек.

Для получения наглядного изображения поверхности на чертеже закон перемещения линии целесообразно задавать графически в виде совокупности линий и указаний о характере перемещения линии. Эти указания могут быть заданы графически, в частности с помощью направляющей поверхности. В процессе образования поверхностей линия может оставаться неизменной или менять свою форму. Такой способ образования поверхности называется кинематическим, а сама поверхность − кинематической. Закон перемещения образующей линии, как правило, задается при помощи направляющих линий и алгоритма перемещения образующей по направляющим.

На чертеже кинематическая кривая поверхность задается при помощи ее определителя. Определителем поверхности называют совокупность условий, необходимых и достаточных для задания поверхности в пространстве.

Подвижная линия называется образующей, неподвижные линии и поверхность – направляющими.

Примером такого способа образования могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» профиля резца.

Режущие кромки являются неотъемлемой частью исполнительных механизмов многих строительных и дорожных машин, применяемых не только для разработки и перемещения грунта (бульдозеры, грейдеры и т. п.), но и рытье траншей, котлованов, проходка траншей, профилирование откосов и многое другое.

Но режущие кромки во многих случаях начинают уступать место производящей поверхности, с которой связано развитие прогрессивных производительных процессов обработки металлов давлением и обкаткой. Геометрическая сущность этих процессов – метод огибания.

Рассмотрим некоторые кривые поверхности.

Кривые поверхности широко применяются в различных областях науки и техники при создании очертаний различных технических форм или как объекты инженерных исследований. Существуют три способа задания кривых поверхностей:

2. При помощи каркаса;

3. Кинематический, т. е. перемещением линий в пространстве.

.

Рис. 7.1. Пример поверхности, заданной аналитически

Составлением уравнений поверхностей занимается аналитическая геометрия; она рассматривает кривую поверхность как множество точек, координаты которых удовлетворяют некоторому уравнению. На рис. 7.1 приведен пример поверхности, за­данной аналитически (системой алгебраических уравнений).

При каркасном способе задания кривая поверхность задается совокупностью некоторого количества линий, принадлежащих поверхности.

Каркас поверхности

Другим способом образования поверхности и ее изображения на чертеже может служить каркас поверхности.

Каркасом поверхности принято называть упорядоченное множество точек или линий, принадлежащих поверхности.

В зависимости от того, чем задается каркас поверхности, точками или линиями, каркасы называют точечными или линейными. Линейным каркасом называется множество таких линий, которые имеют единый закон образования и связаны между собой определенной зависимостью. Условия связи между линиями каркаса называются зависимостью каркаса. Эта зависимость характеризуется некоторой изменяющейся величиной, которая называется параметром каркаса. Если параметр линейного каркаса является непрерывной функцией, то каркас называется непрерывным, а если параметр − прерывная функция, то каркас называется дискретным.

На рис. 7.2 приведен пример каркаса поверхности, состоящей из двух ортогонально расположенных семейств линий а₁, а₂, а₃,…, а_n, b₁, b₂, b₃,…b_n.

.

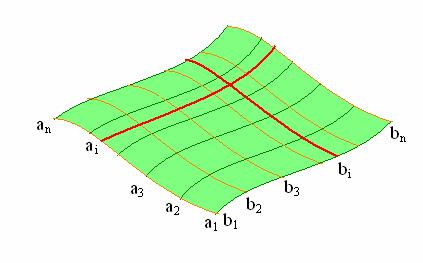
Рис. 7.2. Пример линейного каркаса поверхности

Определитель поверхности

Кинематический способ образования поверхности можно представить как множество положений движущейся линии или поверхности.

Этот способ дает возможность сформулировать понятие определителя поверхности. Под этим понятием обычно подразумевают необходимую и достаточную совокупность геометрических фигур и кинематических связей между ними, которые однозначно определяют поверхность.

Определитель поверхности состоит из двух частей:

Чтобы найти определитель поверхности, следует исходить из кинематического способа образования поверхности.

Для того чтобы построить чертеж поверхности, необходимо предварительно выявить ее определитель. Определитель поверхности выявляется путем анализа способов образования поверхности или ее основных свойств. В общем случае поверхность может быть образована несколькими способами и поэтому может иметь несколько определителей. Обычно из всех способов образования поверхности выбирают простейший.

Поверхность считается заданной на комплексном чертеже, если относительно любой точки пространства, заданной на чертеже, можно однозначно решить вопрос о принадлежности ее данной поверхности. Построение проекций любых точек и линий, принадлежащих поверхности, а также второй их проекции, если одна задана, выполняется на основании ее определителя.

Точка принадлежит поверхности, если она принадлежит линии, принадлежащей поверхности.

Рассмотрим примеры выявления определителя для некоторых простейших поверхностей:

Через три точки А, В, С, не принадлежащие одной прямой, можно провести одну и только одну плоскость ( 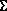на рис. 7.3, а). Точки А, В и С составляют геометрическую часть определителя плоскости.

Вторая часть определителя, т. е. алгоритм построения в плоскости 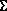(А, В, С) любых линий и точек, выражается рассмотренными ранее условиями принадлежности прямой и точки плоскости.

На чертеже (рис. 7.3, б) плоскость 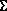задана проекциями геометрической части своего определителя: А(А₁А₂), В(В₁В₂), С(С₁С₂).

Цилиндрическая поверхность вращения может быть образована вращением прямой l i вокруг оси i (рис. 7.4, а).

Геометрическая часть определителя поверхности состоит из образующей l и оси i. Алгоритмическая часть определителя состоит из операции вращения образующей линии l вокруг оси i.

Определитель цилиндрической поверхности вращения имеет вид Ф(l i, i) [А]. На чертеже (рис. 7.4, б) цилиндр вращения задан проекциями геометрической части своего определителя.

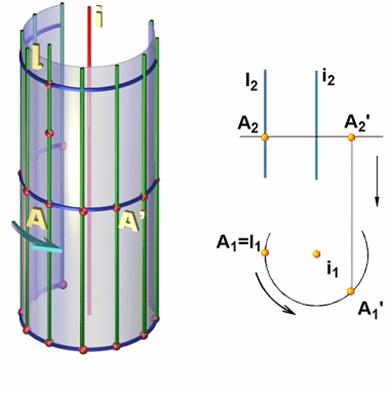
Коническая поверхность вращения может быть образована вращением прямой l, пересекающей ось вращения i под некоторым углом (рис. 7.5, а). Алгоритмическая часть определителя состоит из словесного указания о том, что поверхность образуется вращением образующей l вокруг оси i.

.

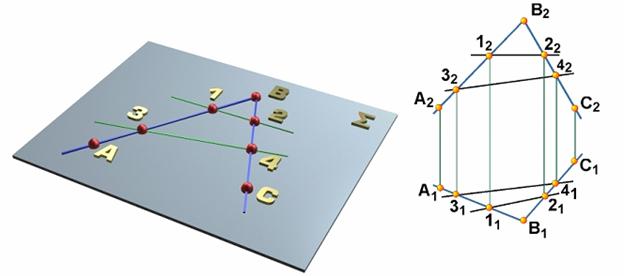
Рис.7.3. Примеры определителя: а − алгоритмическая часть; б − геометрическая часть

Определитель конической поверхности вращения имеет вид Ф(l i)[A].

На чертеже (рис. 7.5, б) конус вращения задан проекциями геометрической части его определителя:

l(l₁l₂) 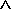i(i₁i₂>

В указанных примерах определитель поверхности выявляется путем анализа способов ее образования. Рассмотрим пример выявления определителя поверхности путем анализа ее основных свойств. Возьмем, например, сферу. Сферой называется поверхность, образованная множеством точек пространства, находящихся на расстоянии | r | от данной точки O (рис. 7.6, а). Геометрическая часть определителя сферы состоит из точки O (центра сферы) и точки М, принадлежащей ее поверхности. Алгоритм построения любой точки сферы заключается в проведении через точку О произвольной прямой и откладывания на ней от точки О отрезка | OM’ = | ОМ | = | r |. Определитель сферы имеет вид Ф(О, М) [А].

.

На рис. 7.6, б (справа) сфера задана проекциями точек О(O₁O₂) и М(М₁М₂), которые составляют геометрическую часть ее определителя, и показано построение произвольной точки М n (М n ₁ М n ₂)сферы.

При чтении чертежа немаловажную роль играет его наглядность. Задание поверхности проекциями геометрической части ее определителя не обеспечивает наглядности изображений. Поэтому для придания чертежу поверхности большей наглядности и выразительности прибегают к построению очерков ее проекций или проекций достаточно плотного каркаса ее образующих.

При проецировании поверхности на какую-либо плоскость проекций часть проецирующих лучей касается ее, образуя проецирующую поверхность. Точки касания при этом образуют линию видимого контура поверхности относительно этой плоскости проекций (рис. 7.7). Очерк проекции поверхности является проекцией соответствующей линии видимого контура.

Линия видимого контура поверхности разделяет ее на две части − видимую, обращенную к наблюдателю, и невидимую. Никакая точка поверхности не может спроецироваться за пределы очерка.

.

На чертежах (рис. 7.8, а, в) конус вращения и сфера заданы проекциями геометрической части своего определителя, а на чертежах (рис. 7.8, б, г) для тех же поверхностей построены очерки их проекций. Последние, безусловно, обладают большей наглядностью и выразительностью.

Кривые поверхности разделяются на линейчатые и нелинейчатые, закономерные и незакономерные. Поверхность называется линейчатой, если она может быть образована перемещением прямой линии, в противном случае − нелинейчатой.

Если поверхность может быть задана каким-либо уравнением, она называется закономерной, в противном случае − незакономерной, или графической (задается только чертежом).

Закономерные поверхности, в зависимости от вида уравнения, разделяются на алгебраические и трансцендентные.

Алгебраическое уравнение n-й степени (в декартовых координатах) задает алгебраическую поверхность n-го порядка (трансцендентные поверхности порядка не имеют). Алгебраическая поверхность n-го порядка пересекается плоскостью по кривой n-го порядка, а с прямой линией − в n точках.

.

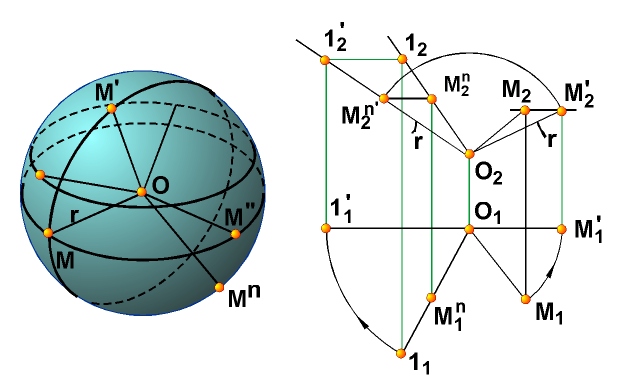
Рис. 7.6. Изображение определителя сферы: а – алгоритмическая часть; б – геометрическая часть

Плоскость, имеющую уравнение первой степени (с произвольной плоскостью пересекается по прямой линии, а с прямой − в одной точке), можно рассматривать как поверхность первого порядка. Примерами кривых поверхностей второго порядка могут служить поверхности, образованные вращением кривых второго порядка вокруг одной из своих осей.

Поверхности второго порядка пересекаются с произвольной плоскостью по кривым второго порядка, а с прямой − в двух точках. Примером поверхности четвертого порядка может служить тор (см. поверхности вращения).

.

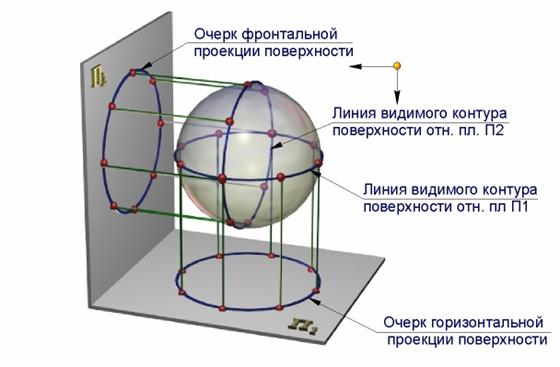
Рис. 7.7. Образование проекций сферы

.

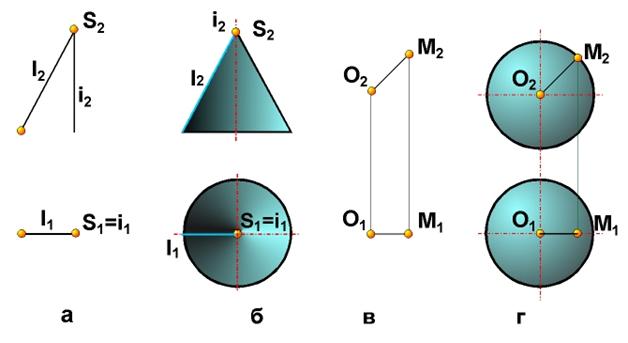
Рис. 7.8. а, в − проекции геометрической части определителей конуса и сферы; б, г − очерки проекций конуса и сферы

Определитель может быть положен в основу классификации поверхностей. К одному и тому же классу относятся поверхности, имеющие одинаковую структуру определителя.

Наибольшее применение в технике получили кинематические кривые поверхности с образующими постоянной формы:

1. Линейчатые поверхности:

Источник

ПОВЕРХНОСТЬ

ПОВЕРХНОСТЬ, одно из основных геометрич. понятий. При логич. уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.

Смотреть что такое ПОВЕРХНОСТЬ в других словарях:

ПОВЕРХНОСТЬ

(Surface, Oberfläche). — Всякую непрерывную кривую линию можно представить, как след движущейся точки. Подобно этому и всякую П. можно образовать или о. смотреть

ПОВЕРХНОСТЬ

ПОВЕРХНОСТЬ

ПОВЕРХНОСТЬ

поверхность 1. ж. 1) а) Наружная сторона чего-л. б) Верхний слой массы какого-л. вещества, жидкости и т.п. 2) Совокупность неровностей земной коры, образующих низменности, возвышенности и т.п.; рельеф (в географии). 2. ж. 1) а) Граница, отделяющая геометрическое тело от внешнего пространства или от другого тела (в геометрии). б) След движения какой-л. линии в пространстве. 2) Сторона плоскости или твердого тела, пересекающаяся с другими сторонами под углом; грань. 3. ж. устар. Преимущество, превосходство над кем-л. (в борьбе, споре и т.п.).

ПОВЕРХНОСТЬ

ПОВЕРХНОСТЬ

ПОВЕРХНОСТЬ

Поверхность (Surface, Oberflä che). — Всякую непрерывную кривую линию можно представить, как след движущейся точки. Подобно этому и всякую П. можно образовать или описать движением в пространстве некоторой кривой линии неизменяемого или изменяемого вида и размеров, и притом способ образования П. может быть разнообразен. Например, всякая П. вращения может быть получена вращением надлежащей плоской кривой вокруг оси, находящейся в одной с нею плоскости, и та же П. может быть описана окружностью круга, радиус которого изменяется по надлежащему закону, а плоскость которого движется поступательно вместе с центром, движущимся по оси вращения, перпендикулярной к плоскости круга. Из этого видно, что вид П. может быть еще более разнообразен, чем вид кривых. Наглядное представление о виде П. труднодостижимо помощью рисунков и чертежей, столь удобных для представления плоских кривых линий. Лучшим средством для наглядного представления П. служат модели, металлические, деревянные. гипсовые и др. Предмет учения о П. разного рода, теперь известных и изученных, очень обширен, и в настоящей статье придется ограничиться указанием на некоторые виды II., более известные и чаще встречающиеся. Многие П. могут быть аналитически представлены уравнениями вида: f(x, у, z) = 0, выражающими зависимость между координатами (см.) точек, принадлежащих П. Иногда П. выражается двумя уравнениями, заключающими, кроме координат, еще четвертую переменную величину, имеющую значение параметра кривой линии, которая своим движением образует П.; в таком случае уравнение П. должно получиться, по исключении этого переменного параметра, из двух уравнений. Наконец, случается, что координаты точек П. выражены функциями двух переменных параметров, тогда уравнение П. должно быть результатом исключения этих параметров из трех уравнений. Если f(x, y, z) есть функция алгебраическая, то П. называется алгебраической, а если в этой функции заключаются функции трансцендентные, то П. называется трансцендентной. Соответственно степени уравнения, алгебраические П. разделяются на порядки. П. первого порядка суть плоскости. П. второго порядка: эллипсоиды, шары, гиперболоиды об одной и двух полах, параболоиды эллиптические и гиперболические, цилиндрические и конические П. второго порядка рассматриваются в любом курсе аналитической геометрии в пространстве. П. третьего порядка рассматривались и исследовались с 30-х годов настоящего столетия многими авторами; таково, например, исследование проф. Клейна («Mathem. Annal.», т. VI), в котором П. эти разделены на несколько классов, начиная с таких, на которых лежат 27 прямых линий. П. четвертого порядка также были предметом изучения некоторых математиков, и построены модели многих П. третьего порядка и некоторых четвертого порядка. Наконец, встречаются исследования касательно П. высшего порядка, такова, напр., алгебраическая П. девятого порядка, открытая Эннепером и принадлежащая к числу П. minima, т. е. таких, средняя кривизна которых равна нулю. Гиперболоиды об одной поле и параболоиды гиперболические принадлежат к классу линейчатых поверхностей (см.), к которым принадлежат еще всевозможные П. цилиндрические (см.), конические (см.), линейчатые коноиды (см.), линейчатые геликоиды (см.). Гиперболоид об одной поле и параболоид гиперболический имеют по две системы прямолинейных производящих. Линейчатые П. могут быть разделены на два разряда: развертываемые на плоскость и косые. К первым принадлежат: все цилиндрические, все конические П. и геликоид, развертываемый на плоскость (см.). К косым принадлежат вышесказанные гиперболоид и параболоид и обыкновенная винтовая П., производящие которой перпендикулярны к оси (см.). Эта П. есть вместе с тем и коноид и одна из П. minirna. П. minima названы так потому, что занимают собою наименьшую площадь при заданном контуре; в каждой точке такой П. сумма главных кривизн, или средняя кривизна П., равна нулю, а поэтому они могут быть воспроизведены пластинчатой (см. Пластинчатое состояние жидкости) поверхностью мыльной воды по способу Плато. Существует весьма большая литература по вопросу о П. Minima. В книге Дарбу «Le çons sur théorie générale des surfaces» (4 тт.) можно найти весьма полное изложение по теории П. Minima. В числе П. Mmima есть катеноид, т. е. П., образуемая вращением цепной линии (см. соотв. ст.; см. табл. Кривые, черт. 3) вокруг ее оси абсцисс. Этот катеноид может быть наложен без разрыва и складок на вышесказанную винтовую линейчатую П. таким образом, что обратившаяся в прямую линию окружность шейки катеноида ляжет вдоль оси винта и все кривые меридиональных сечений катеноида обратятся в прямые, которые лягут по производящим. Катеноид есть единственная минимальная П. вращения. П. с постоянною средней кривизной принадлежат к числу тех, которыми может быть ограничена П. жидкости, не подверженной действию внешних сил. К числу таких П., кроме катеноида, принадлежат две П. вращения: ундулоид и нодоид. Из числа П. с постоянной полной отрицательной кривизной мы укажем на одну П. вращения, меридиональное сечение которой есть трактриса, или трактория (см.; см. также таблицу Кривые, черт. 12, левая фигура); эта П. называется псевдосферою (см.), потому что, подобно как на сфере, можно переносить фигуру, начерченную на ней, на другую часть П. с сохранением длин дуг, углов и величин площадей. О величинах площадей замкнутых П. (см.). Д. Б.

ПОВЕРХНОСТЬ

34 поверхность: Двухмерный пространственный объект, образованный в своих границах набором значений функции двухмерных координат в виде непрерывного п. смотреть

ПОВЕРХНОСТЬ

area, (напр. лакокрасочного покрытия) finish, surface* * *пове́рхность ж.surface; (площадь) area; (плоскость) plane, faceвыступа́ть на пове́рхности (. смотреть

ПОВЕРХНОСТЬ

Атомная структура кристалла с ковалентнымисвязями (двойные линии). Соседние атомы поверхностного слоя (светлые кружки)образуют связи между собой, объединяясь в димеры. При этом на поверхностипериод решётки равен 2d (реконструкция 2 х 1). Кроме того, межплоскостноерасстояние уменьшается на величину (релаксация).

Особенности атомной структуры характернытакже для границ раздела между двумя конденсиров. средами. В пограничномслое жидкости (толщиной

Магнитные свойства П. Теория предсказываетотличие намагниченности поверхностного слоя, а также темп-ры магн. фазовыхпереходов на П. от соответствующих объёмных значений. Эксперим. исследованиямагнетизма П. осуществляются методами дифракции медленных поляризов. электронов, квантовых магнитометров, чувствительность к-рыхдостаточна для измерения намагниченности отд. монослоёв вещества.

Поверхностная энергия. П. обладаетнек-рой избыточной поверхностной энергией, т. к. образование П. требуетразрыва или перестройки связей между атомами или молекулами в конденсиров. фаза, необходимость затратыэнергии на образование межфазной П. приводит к явлениям перегрева или переохлаждения(см. Кипение, Кристаллизация).
Равновесное состояние системы конечныхразмеров определяется (при пост. объёме) минимумом суммарной свободнойэнергии, в к-рую вносит вклад как объём, так и П., причём относительныйвклад П. изменяется обратно пропорц. размеру объекта. Уменьшение поверхностнойсвободной энергии, происходящее за счёт тех или иных изменений П. (сокращенияеё площади, понижения энергии в результате насыщения свободных связей поверхностныхатомов и молекул и т. д.), служит движущей силой таких поверхностных явлений, адсорбция, смачивание, растекание, адгезия и коге-зия, коагуляцияакустическая, образование капель, капиллярные явления и др. скорость испарениявещества подложки, хим. активность П. по отношению к разл. реакциям. Ввеществах, у к-рых адсорбция уменьшает поверхностную энергию, облегчаетсяобразование дефектов, тем самым понижается прочность твёрдых тел (см. Ребиндераэффект). Адсорбция стимулирует также образование эмульсий и пен (см.Поверхностно-активныевещества).

Экспериментальные методы, дающиеинформацию о поверхностных явлениях на атомном уровне, разнообразны. Этоавтоэмиссионная микроскопия (см. Ионный проектор), дифракция электронов, инфракраснаяспектроскопия, ионная спектроскопия, комбинационное рассеяние света, сканирующая туннельная микроскопия, термодесорбц. фотоэлектронная спектроскопия, электронная микроскопия, электрон-фотоннаяспектроскопия, эллипсометрия и др. Эти методы позволяют решать мн. микроэлектроники.

Источник