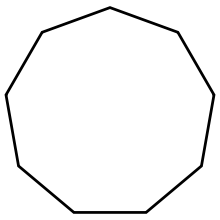
Что такое правильный десятиугольник
Десятиугольник
| Правильный десятиугольник | |
|---|---|
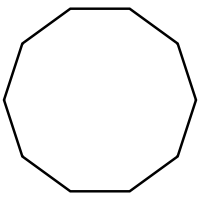 | |
| Рёбра и вершины | 10 |
| Площадь |    |
| Внутренний угол (градусы) | 144° |
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами.
Площадь правильного десятиугольника вычисляется следующим образом:
Внешние ссылки
Планигон
Полезное
Смотреть что такое «Десятиугольник» в других словарях:
десятиугольник — декагон Словарь русских синонимов. десятиугольник сущ., кол во синонимов: 3 • декагон (1) • … Словарь синонимов
ДЕСЯТИУГОЛЬНИК — ДЕСЯТИУГОЛЬНИК, десятиугольника, муж. (геом.). Замкнутый многоугольник с десятью сторонами. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
десятиугольник — (10 угольник) … Орфографический словарь-справочник
Десятиугольник — (мат.) Разделяя окружность круга на 10 равных частей, получим десять точек. Если мы соединим точки последовательно одну за другой прямыми линиями, то получим Д., так называемый правильный, вписанный в круг. Если же соединим прямыми линиями точки… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Десятиугольник — м. 1. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей десять углов. 2. Пространство или предмет такой формы. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
десятиугольник — десятиугольник, десятиугольники, десятиугольника, десятиугольников, десятиугольнику, десятиугольникам, десятиугольник, десятиугольники, десятиугольником, десятиугольниками, десятиугольнике, десятиугольниках (Источник: «Полная акцентуированная… … Формы слов
десятиугольник — десятиуг ольник, а … Русский орфографический словарь
десятиугольник — (2 м); мн. десятиуго/льники, Р. десятиуго/льников … Орфографический словарь русского языка
десятиугольник — а; м. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей десять углов. Начертить д … Энциклопедический словарь
десятиугольник — а; м. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей десять углов. Начертить десятиуго/льник … Словарь многих выражений
Десятиугольник: правильный, неправильный, свойства, примеры
В десятиугольник представляет собой плоскую фигуру в форме многоугольника с 10 сторонами и 10 вершинами или точками. Десятиугольники могут быть правильными или неправильными, в первом случае все сторо
Содержание
В десятиугольник представляет собой плоскую фигуру в форме многоугольника с 10 сторонами и 10 вершинами или точками. Десятиугольники могут быть правильными или неправильными, в первом случае все стороны и внутренние углы имеют одинаковую величину, а во втором стороны и / или углы отличаются друг от друга.
На рисунке 1 показаны примеры десятиугольника каждого типа, и, как мы видим, правильный десятиугольник очень симметричен.
Рис. 1. Слева правильный десятиугольник, а справа неправильный десятиугольник. Источник: Wikimedia Commons / Ф. Zapata / Mathopenref.
Основными элементами каждого десятиугольника являются:
-Стороны, отрезки прямых, которые при соединении образуют десятиугольник.
-Vertices или точки между каждой последовательной стороной.
-Внутренние и внешние углы между соседними сторонами.
-Диагональные, сегменты, соединяющие две непоследовательные вершины.
Вершины обозначаются заглавными буквами, как показано на рисунке 1, где использовались первые буквы алфавита, но можно использовать любую букву.
Обычный десятиугольник
В правильном десятиугольнике все стороны имеют одинаковую меру, как и внутренние углы. Поэтому говорят, что это равносторонний (равные стороны) и равносторонний (равные углы). Это очень симметричная фигура
Внутренние углы правильного десятиугольника
Чтобы найти меру внутренних углов правильного многоугольника, включая правильный десятиугольник, используется следующая формула:
Подставляя n = 10 в предыдущую формулу, получаем следующее:
Говорят, что многоугольник выпуклый если его угловые размеры меньше 180 °, в противном случае многоугольник вогнутый. Поскольку любой внутренний угол правильного десятиугольника составляет 144º и меньше 180º, то это выпуклый многоугольник.
Сумма внутренних углов
Сумма внутренних углов любого многоугольника в градусах:
S = (n-2) x 180 °; n всегда больше 2
В этой формуле мы имеем:
Применяя формулу для n = 10 результатов:
S = (10–2) x 180º = 1440º
Внешние углы
Между одной стороной и продолжением соседней стороны образуется внешний угол, посмотрим:
Рисунок 2.- Внешний угол правильного десятиугольника составляет 36º. Источник. Wikimedia Commons / Ф. Сапата.
Сумма угла ∠ ABC плюс внешний угол составляет 180 °, то есть они равны дополнительный. Следовательно, внешний угол равен 180º-144º = 36º, как мы видим на рисунке.
Количество диагоналей
К счастью, есть формула, по которой можно узнать количество диагоналей многоугольника. п стороны:
Подставляем десятиугольник n = 10 и получаем:
В правильном десятиугольнике все диагонали пересекаются в одной точке, которая является центром фигуры:
Рис. 3. Углы и диагонали правильного десятиугольника. Источник: Wikimedia Commons.
Центр
Центр многоугольника определяется как точка, равноудаленная от любой вершины. На рисунке выше центр совпадает с точкой пересечения всех диагоналей.
Периметр
Если у правильного десятиугольника есть сторона a, его периметр P равен сумме всех сторон:
Площадь
Зная длину к сбоку площадь правильного десятиугольника рассчитывается по формуле:
Примерная формула для площади:
В таком случае площадь можно рассчитать по формуле:
Неправильный десятиугольник
Неправильный десятиугольник не является равносторонним или равноугольным, и, как правило, ему не хватает симметрии правильной фигуры, хотя некоторые декагоны могут иметь ось симметрии.
Они также могут быть выпуклыми или вогнутыми, если внутренние углы превышают 180º.
Неправильный десятиугольник на фиг. 1 вогнут, так как некоторые из его внутренних углов больше 180 °. Очевидно, что существует множество комбинаций углов и сторон, которые приводят к неправильному десятиугольнику.
В любом случае верно то, что:
-Внутренние углы неправильного десятиугольника также составляют 1440º.
-Также имеет 35 диагоналей.
Площадь неправильного десятиугольника по гауссовским определителям
В общем, не существует единой формулы для определения площади неправильного многоугольника, поскольку стороны и углы разные. Однако его можно найти, зная координаты вершин и вычисливГауссовские детерминанты:
-Вы можете начать с любой вершины, до которой координаты (x1, а также1 ). Теперь нам нужно подставить значения каждой координаты в эту формулу:
-Важно отметить, что последний определитель снова включает первую вершину вместе с последней. Для десятиугольника это будет выглядеть так:
Важный: Полоски имеют абсолютное значение и означают, что окончательный результат дается с положительным знаком. навсегда.
Упражнение решено
Рис. 4. Неправильный десятиугольник и его вершины. Источник: Ф. Сапата с Geogebra.
Решение
-Делаем каждую из 10 операций:
-Давайте добавим результаты:
12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124
Положительный результат получается даже без столбцов абсолютного значения, но если он отрицательный, знак меняется.
-Предыдущий результат делится на 2, и это площадь многоугольника:
Свойства Десятиугольника
Вот краткое изложение общих свойств десятиугольника, правильного или неправильного:
-У него 10 сторон и 10 вершин.
-Сумма внутренних углов 1440º.
-Есть 35 диагоналей.
-Периметр складывается из всех сторон.
-Вы можете создавать треугольники внутри многоугольника, рисуя сегменты от одной вершины ко всем остальным. В десятиугольнике можно нарисовать 8 треугольников, как показано ниже:
Рис. 5. Внутренние треугольники в правильном десятиугольнике. Источник: Матопенреф.
Правильный десятиугольник
| Правильный десятиугольник | |
|---|---|
 | |
| Сторон и вершин | 10 |
| Символ Шлефли | |
| Внутренний угол | 144° |
| Симметрия | Диэдрическая ( D 10 <\displaystyle D_<10>>  ), порядок 20. ), порядок 20. |
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Содержание
Правильный десятиугольник
У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.
Площадь правильного десятиугольника равна (t — длина стороны):
и может быть представлен в радикалах как
Радиус описанной окружности десятиугольника равен
а радиус вписанной окружности
Построение
По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку. На диаграмме показано одно из таких построений. Иначе его можно построить следующим образом:
Разбиение правильного десятиугольника
| Разбиение правильного десятиугольника | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ортогональные проекции многогранников | |||
|---|---|---|---|
 Додекаэдр Додекаэдр |  Икосаэдр Икосаэдр |  Икосододекаэдр Икосододекаэдр |  Ромботриаконтаэдр Ромботриаконтаэдр |
Многоугольники Петри
Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.
Десятиугольник: правильный, неправильный, свойства, примеры
Содержание:
В десятиугольник представляет собой плоскую фигуру в форме многоугольника с 10 сторонами и 10 вершинами или точками. Декагоны могут быть правильными или неправильными, в первом случае все стороны и внутренние углы имеют одинаковую величину, а во втором стороны и / или углы отличаются друг от друга.
На рисунке 1 показаны примеры десятиугольника каждого типа, и, как мы видим, правильный десятиугольник очень симметричен.
Основными элементами каждого десятиугольника являются:
-Стороны, отрезки линии, которые при соединении образуют десятиугольник.
-Vertices или точки между каждой последовательной стороной.
-Внутренние и внешние углы между соседними сторонами.
-Диагональные, сегменты, соединяющие две непоследовательные вершины.
Вершины названы заглавными буквами, как показано на рисунке 1, где использовались первые буквы алфавита, но можно использовать любую букву.
Обычный десятиугольник
В правильном десятиугольнике все стороны имеют одинаковую меру, как и внутренние углы. Поэтому говорят, что это равносторонний (равные стороны) и равносторонний (равные углы). Это очень симметричная фигура
Внутренние углы правильного десятиугольника
Чтобы найти меру внутренних углов правильного многоугольника, включая правильный десятиугольник, используется следующая формула:
Подставляя n = 10 в предыдущую формулу, получаем следующее:
Говорят, что многоугольник выпуклый если его угловые размеры меньше 180 °, иначе многоугольник вогнутый. Поскольку любой внутренний угол правильного десятиугольника составляет 144º и меньше 180º, то это выпуклый многоугольник.
Сумма внутренних углов
Сумма внутренних углов любого многоугольника в градусах:
S = (n-2) x 180 °; n всегда больше 2
В этой формуле мы имеем:
Применяя формулу для n = 10, получаем:
Внешние углы
Между одной стороной и продолжением соседней стороны образуется внешний угол, посмотрим:
Сумма угла ∠ ABC плюс внешний угол составляет 180 °, то есть они равны дополнительный. Следовательно, внешний угол равен 180º-144º = 36º, как мы видим на рисунке.
Количество диагоналей
К счастью, есть формула, по которой можно узнать, сколько диагоналей многоугольника. п стороны:
Подставляем десятиугольник n = 10 и получаем:
В правильном десятиугольнике все диагонали пересекаются в одной точке, которая является центром фигуры:
Центр
Центр многоугольника определяется как точка, равноудаленная от любой вершины. На рисунке выше центр совпадает с точкой пересечения всех диагоналей.
Периметр
Если у правильного десятиугольника есть сторона a, его периметр P равен сумме всех сторон:
Площадь
Зная длину к сбоку площадь правильного десятиугольника рассчитывается по формуле:
Приблизительная формула для площади:
В этом случае площадь можно рассчитать по формуле:
Неправильный десятиугольник
Неправильный десятиугольник не является равносторонним или равноугольным, и обычно ему не хватает симметрии правильной фигуры, хотя некоторые десятиугольники могут иметь ось симметрии.
Они также могут быть выпуклыми или вогнутыми, если внутренние углы превышают 180º.
Неправильный десятиугольник на фиг. 1 вогнут, поскольку некоторые из его внутренних углов больше 180 °. Ясно, что существует множество комбинаций углов и сторон, которые приводят к неправильному десятиугольнику.
В любом случае верно, что:
-Внутренние углы неправильного десятиугольника также составляют в сумме 1440º.
-Также имеет 35 диагоналей.
Площадь неправильного десятиугольника по гауссовским определителям
В общем, не существует единой формулы для определения площади неправильного многоугольника, поскольку стороны и углы разные. Однако его можно найти, зная координаты вершин и вычисливГауссовские детерминанты:
-Вы можете начать с любой вершины, до которой координаты (x1, Y1 ). Теперь нам нужно подставить значения каждой координаты в эту формулу:
-Важно отметить, что последний определитель снова включает первую вершину вместе с последней. Для десятиугольника это будет выглядеть так:
Важный: Полоски имеют абсолютное значение и означают, что окончательный результат дается с положительным знаком. всегда.
Упражнение решено
Решение
-Делаем каждую из 10 операций:
-Давайте добавим результаты:
12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124
Положительный результат получается даже без столбцов абсолютного значения, но если он отрицательный, знак меняется.
-Предыдущий результат делится на 2, и это площадь многоугольника:
Свойства Десятиугольника
Вот краткое изложение общих свойств десятиугольника, правильного или неправильного:
-У него 10 сторон и 10 вершин.
-Сумма внутренних углов 1440º.
-Есть 35 диагоналей.
-Вы можете создавать треугольники внутри многоугольника, рисуя сегменты от одной вершины ко всем остальным. В десятиугольнике можно нарисовать 8 треугольников таким образом, как показано ниже:
Ссылки
Греческий театр: история, элементы, костюмы и маски
Автоматонофобия: симптомы, причины и лечение
Правильный девятиугольник
Правильный девятиугольник — это правильный многоугольник с девятью сторонами.
Свойства
Правильный девятиугольник имеет внутренние углы, равные 140°. Площадь правильного девятиугольника со стороной a определяется выражением
Построение
Хотя правильный девятиугольник и невозможно построить с помощью циркуля и линейки, существуют методы построения также достаточно неточных приближений.
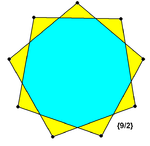
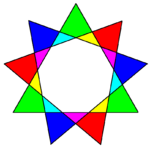
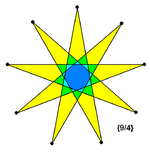
Девятиугольные звёзды
Существует три звёздчатых девятиугольника: <9/2>, <9/3>и <9/4>, причём звезда <9/3>состоит из трёх равносторонних треугольников:
 |
 Правильные многоугольники Правильные многоугольники | |
|---|---|
| Основные | Треугольник • Квадрат • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Семнадцатиугольник • 257-угольник • 65537-угольник |
| См. также | Многоугольник • Теорема Гаусса — Ванцеля |
Полезное
Смотреть что такое «Правильный девятиугольник» в других словарях:
Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
Правильный шестиугольник — (гексагон) это правильный многоугольник с шестью сторонами … Википедия
Правильный треугольник — Правильный треугольник. Правильный (или равносторонний) треугольник это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны … Википедия
Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия
Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание … Википедия
Правильный восьмиугольник — (октагон) геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой … Википедия
Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия
Правильный 257-угольник — 257 угольник или окружность? Правильный 257 угольник правильный многоугольник с 257 сторонами. Содержание … Википедия
Правильный пятиугольник — Иное название этого понятия «Пентагон»; см. также другие значения. Правильный пятиугольник Правильный пятиугольник (греч … Википедия
- Что такое основная и дополнительная погрешности прибора и какими факторами они определяются
- Что такое нервный срыв и как он проявляется