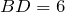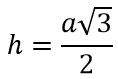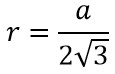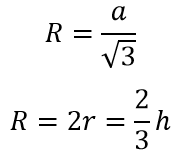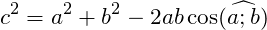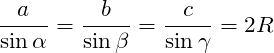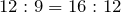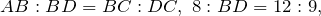Что такое правильный треугольник в геометрии
Правильный треугольник
Связанные понятия
Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.
Упоминания в литературе
Связанные понятия (продолжение)
В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.
Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.
Равносторонний треугольник
Правильный треугольник или равносторонний треугольник — это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60° (или π / 3 ).
В силу определения правильный треугольник также является равнобедренным.
Свойства
Радиус вписанной окружности правильного треугольника, выраженный через его сторону

Радиус описанной окружности правильного треугольника, выраженный через его сторону
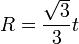
Периметр правильного треугольника равен
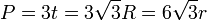
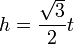
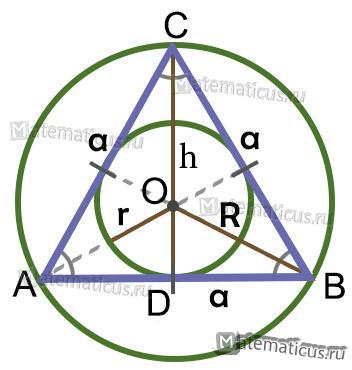
Площадь правильного треугольника рассчитывается по формулам:
| Правильные многоугольники |
|---|
| Треугольник | Четырёхугольник | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Семнадцатиугольник | 257-угольник | 65537-угольник |
| (См. также: Многоугольник, Теорема Гаусса — Ванцеля) |
Полезное
Смотреть что такое «Равносторонний треугольник» в других словарях:
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК — РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК, плоская фигура, имеющая три стороны равной длины; три внутренних угла, образуемых сторонами, также равны и составляют 60 °С. см. также ТРЕУГОЛЬНИК … Научно-технический энциклопедический словарь
ТРЕУГОЛЬНИК — и (прост.) трёхугольник, треугольника, муж. 1. Геометрическая фигура, ограниченная тремя взаимно пересекающимися прямыми, образующими три внутренних угла (мат.). Тупоугольный треугольник. Остроугольный треугольник. Прямоугольный треугольник.… … Толковый словарь Ушакова
Треугольник Серпинского — Треугольник Серпинского фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Серпински … Википедия
РАВНОСТОРОННИЙ — РАВНОСТОРОННИЙ, равносторонняя, равностороннее (мат.). Имеющий стороны равной длины. Равносторонний многоугольник. Равносторонний треугольник. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Треугольник — Триединая природа вселенной: Небо, Земля, Человек; отец, мать, дитя; человек как тело, душа и дух; мистическое число три; тройка, первая из плоских фигур. Отсюда символ поверхности вообще. Поверхность состоит из треугольников (Платон).… … Словарь символов
Треугольник — У этого термина существуют и другие значения, см. Треугольник (значения). Треугольник (в евклидовом пространстве) это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки,… … Википедия
Треугольник Рёло — Построение треугольника Рёло Треугольник Рёло[* 1] предста … Википедия
треугольник — ▲ многоугольник ↑ имеющий, три, угол треугольник простейший многоугольник; задается 3 точками, не лежащими на одной прямой. треугольный. остроугольник. остроугольный. прямоугольный треугольник: катет. гипотенуза. равнобедренный треугольник. ▼… … Идеографический словарь русского языка
ТРЕУГОЛЬНИК — Этим геометрическим термином называется музыкальный инструмент, который входит в группу ударных и довольно часто применяется в симфонической и оперной музыке. По форме инструмент представляет собой равносторонний треугольник. Сделан он из… … Музыкальный словарь
РАВНОСТОРОННИЙ — РАВНОСТОРОННИЙ, яя, ее. Имеющий равные стороны. Р. треугольник. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Равносторонний (правильный) треугольник
Равносторонний или правильный треугольник — треугольник, у которого три стороны равны. Все углы равностороннего треугольника равны.
Равносторонним треугольником называется такой треугольник, у которого все стороны равны, то есть АВ = ВС = АС (рис. 1)
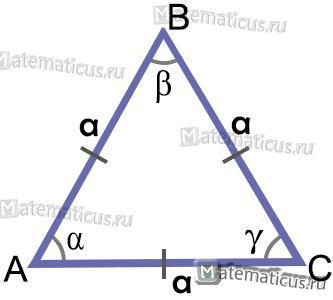
Свойства равностороннего (правильного) треугольника
∠А=∠С=∠В=60°
Из (рис. 2) обозначения:
h — высота=биссектриса=медиана
R — радиус описанной окружности
r — радиус вписанной окружности
a — стороны правильного треугольника
Формула периметра равностороннего треугольника:
Формула площади правильного треугольника:
Формула высоты (или медианы или биссектрисы) равностороннего треугольника:
Радиус вписанной окружности в равносторонний треугольник:
Радиус описанной окружности в равносторонний треугольник:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 5
Треугольник
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:
Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:
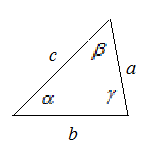
В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.
Отрезок BN — это высота 

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.
Отрезок BN — это биссектриса 
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.
Отрезок BN — это медиана 
Треугольник
Определение треугольника
В любом треугольнике три угла и три стороны.
Против большего угла треугольника лежит большая сторона.
Виды треугольников
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
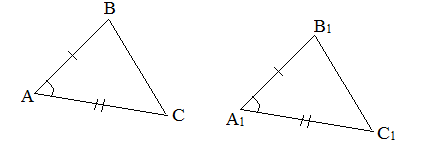
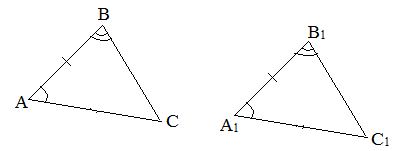
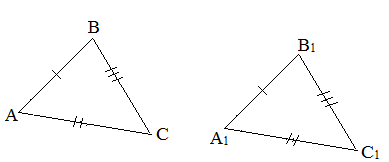
Признаки равенства треугольников
I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Подробнее про признаки равенства треугольников читайте по ссылке.
Признаки подобия треугольников
Треугольники называются подобными, если их стороны пропорциональны.
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Подробнее про признаки подобия треугольников читайте по ссылке.
Теоремы треугольников
Для любого треугольника справедливы следующие теоремы.
Подробнее про теорему косинусов читайте по ссылке.
Подробнее про теорему синусов читайте по ссылке.
Примеры решения задач
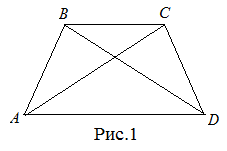
| Задание | Доказать, что в равнобокой трапеции диагонали равны. |
| Доказательство | В равнобокой трапеции  рассмотрим треугольники рассмотрим треугольники  и и 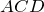 (рис. 1). Так как (рис. 1). Так как 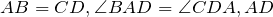 – общая сторона, то треугольники – общая сторона, то треугольники 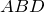 и и 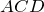 равны по первому признаку, а значит, равны все их элементы, т.е. равны по первому признаку, а значит, равны все их элементы, т.е. 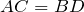 . . |
Что и требовалось доказать.
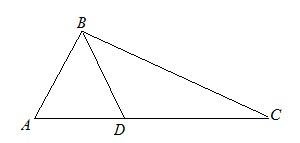
| Задание | В треугольнике 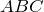 стороны стороны 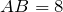 см см 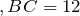 см см 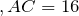 см. На стороне см. На стороне 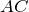 отмечена точка отмечена точка 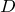 так, чтобы так, чтобы 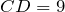 см. Найти отрезок см. Найти отрезок 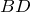 . . |
| Решение | Рассмотрим треугольники 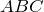 и и 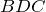 . Запишем отношение сторон . Запишем отношение сторон 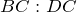 и и 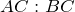 : : |
Так как выполняется равенство отношений, то соответствующие стороны треугольников пропорциональны, а также 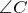
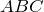
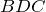
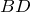
откуда