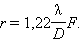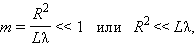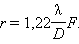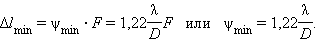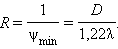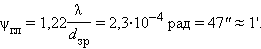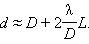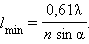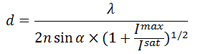Что такое предел разрешения
Что такое предел разрешения
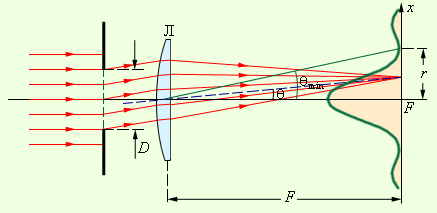
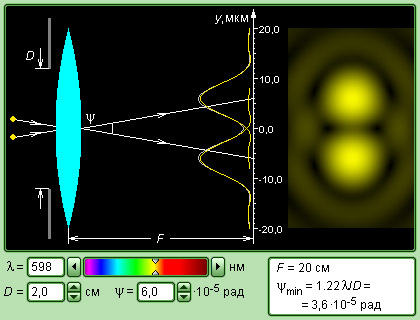
В фокальной плоскости линзы наблюдается дифракционная картина Фраунгофера. Но, согласно геометрической оптике, в фокусе линзы должно располагаться точечное изображение удаленного точечного предмета. На самом деле изображение точечного предмета оказывается размытым из-за дифракции. В этом проявляется волновая природа света.
Никакая оптическая система не может дать точечного изображения. В случае дифракции Фраунгофера на круглом отверстии диаметра дифракционное изображение состоит из центрального светлого пятна (диск Эйри), на которое приходится приблизительно 85 % энергии света, и окружающих его светлых и темных колец (рис. 3.9.2). Это дифракционное пятно и принимается за изображение точечного источника. Радиус центрального пятна в фокальной плоскости линзы равен
|
Если лучи света от удаленного источника падают на линзу непосредственно, то роль экрана, на котором дифрагирует свет, выполняет оправа линзы. В этом случае под нужно понимать диаметр линзы.
Телескоп с диаметром объектива способен разрешать две звезды, находящиеся на угловом расстоянии (для ).
Этот результат хорошо согласуется с физиологической оценкой разрешающей способности глаза, выполненной исходя из размеров светочувствительных элементов сетчатки (палочек и колбочек).
Рис. 3.9.5 качественно показывает, как по мере удаления от препятствия трансформируется пучок света.
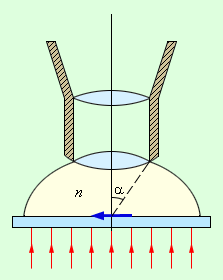
Разрешающая способность микроскопа. С помощью микроскопа наблюдают близко расположенные объекты, поэтому его разрешающая способность характеризуется не угловым, а линейным расстоянием между двумя близкими точками, которые еще могут восприниматься раздельно. Наблюдаемый объект располагается вблизи переднего фокуса объектива. Часто пространство перед объективом заполняется специальной прозрачной жидкостью – иммерсией (рис. 3.9.7). В плоскости, геометрически сопряженной объекту, располагается его увеличенное изображение, которое рассматривается глазом через окуляр. Изображение каждой точки оказывается размытым вследствие дифракции света.
Впервые предел разрешения объектива микроскопа был определен в 1874 г. немецким физиком Г. Гельмгольцем. Формула Гельмгольца имеет вид:
 |
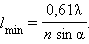Таким образом, с помощью микроскопа принципиально невозможно рассмотреть какие-либо детали, размер которых значительно меньше длины волны света. Волновые свойства света определяют предел качества изображения объекта, полученного с помощью любой оптической системы.
Дифракционный предел разрешения оптических инструментов
Дифракция Фраунгофера. Формулы
Главное условие дифракции Фраунгофера – это наличие зон Френеля, проходящих через точку волны, являющихся плоскими относительно друг друга.
Теперь доступна дифракционная картина Фраунгофера, располагаемая в фокальной плоскости линзы. Исходя из геометрической оптики, фокус должен иметь линзу с точечным изображением удаленного предмета. Изображение такого предмета размывается по причине наличия дифракции. Это и есть проявление волновой природы света.
Оправа линзы обладает свойством дифракции света, если лучи падают на нее, то есть выполняет роль экрана. Тогда D обозначается как диаметр линзы.
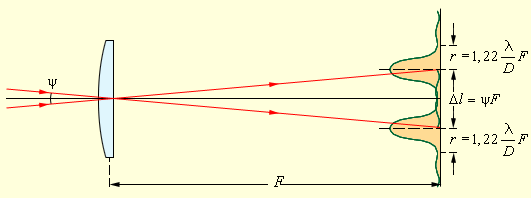
Вышеуказанный рисунок объясняет, что расстояние Δ l между центрами дифракционных изображений звезд превышает значение радиуса r центрального светлого пятна. Данный случай позволяет воспринимать изображение раздельно, значит, есть возможность видеть одновременно две близко расположенные звезды.
Разрешающая способность микроскопа
Предел разрешения объектива микроскопа был определен в 1874 г Г. Гельмгольцем. Такая формула записывается:
Знак λ требуется для обозначения длины волны, n – для показателя преломления иммерсионной жидкости, α – для обозначения апертурного угла. Величину n · sin α называют числовой апертурой.
Отсюда следует, что микроскоп не дает полной возможности просмотра каких-либо деталей с размерами намного менее размера длины световой волны. Волновые свойства света влияют на предел качества изображения объекта, который получаем с помощью любой оптической системы.
Дифракционный предел разрешения оптических инструментов
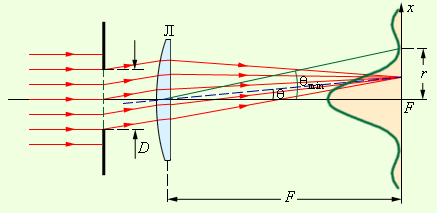
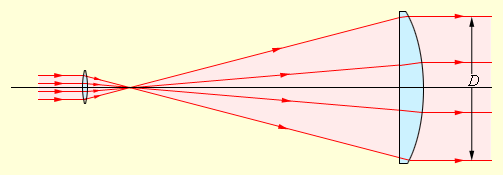
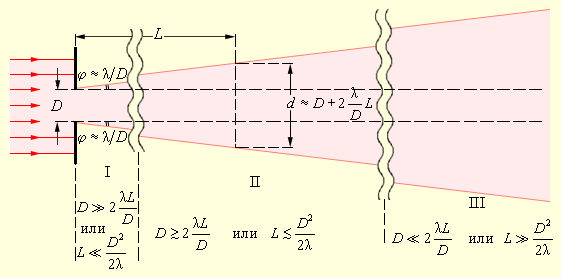
Для практики наиболее интересен случай дифракции света, когда препятствие оставляет открытой лишь малую часть 1-й зоны Френеля. Этот случай реализуется при условии
т. е. дифракционную картину от препятствий небольшого размера следует в этом случае наблюдать на очень больших расстояниях. Например, если R = 1 мм, λ = 550 нм (зеленый свет), то расстояние L до плоскости наблюдения должно быть значительно больше 2 метров (т. е. минимум 10 метров или больше). Лучи проведенные в далекую точку наблюдения от различных элементов волнового фронта, практически можно считать параллельными. Этот случай дифракции так и называется – дифракция в параллельных лучах или дифракция Фраунгофера – по имени немецкого физика И. Фраунгофера, современника Френеля. Если на пути лучей за препятствием поставить собирающую линзу, то параллельный пучок лучей, дифрагировавший на препятствии под углом θ, соберется в некоторой точке фокальной плоскости (рис. 3.9.1). Следовательно, любая точка в фокальной плоскости линзы эквивалентна бесконечно удаленной точке в отсутствие линзы.
Рисунок 3.9.1. Дифракция в параллельных лучах. Зеленая кривая – распределение интенсивности в фокальной плоскости (масштаб по оси x сильно увеличен)
Для подробного ознакомления с медицинской и исследовательской техникой основных мировых производителей оптических систем и сопутствующего оборудования посетите наш каталог или свяжитесь с нашими специалистами и получите полную профессиональную консультацию по любым, имеющимся у Вас, вопросам.
В фокальной плоскости линзы наблюдается дифракционная картина Фраунгофера. Но, согласно геометрической оптике, в фокусе линзы должно располагаться точечное изображение удаленного точечного предмета. На самом деле изображение точечного предмета оказывается размытым из-за дифракции. В этом проявляется волновая природа света.
Никакая оптическая система не может дать точечного изображения. В случае дифракции Фраунгофера на круглом отверстии диаметра D дифракционное изображение состоит из центрального светлого пятна (диск Эйри), на которое приходится приблизительно 85 % энергии света, и окружающих его светлых и темных колец (рис. 3.9.2). Это дифракционное пятно и принимается за изображение точечного источника. Радиус центрального пятна в фокальной плоскости линзы равен
Если лучи света от удаленного источника падают на линзу непосредственно, то роль экрана, на котором дифрагирует свет, выполняет оправа линзы. В этом случае под D нужно понимать диаметр линзы.
Рисунок 3.9.2. Дифракционное изображение точечного источника (дифракция на круглом отверстии). В центральное пятно попадает приблизительно 85 % энергии света
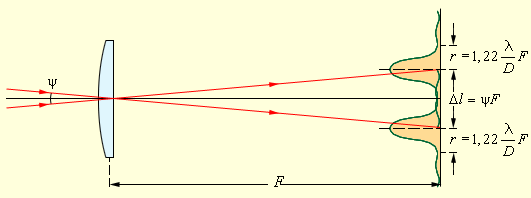
Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Во многих оптических устройствах (фотоаппараты, проекторы и т. д.) дифракционное размытие изображений маскируется значительно более сильными искажениями из-за несовершенства оптики. Но в высокоточных астрономических приборах реализуется дифракционный предел качества изображений. Вследствие дифракционного размытия изображения двух близких точек объекта могут оказаться неотличимы от изображения одной точки. Рассмотрим в качестве примера объектив астрономического телескопа, нацеленного на две близкие звезды, находящиеся на угловом расстоянии ψ друг от друга. Предполагается, что все дефекты и аберрации устранены, и в фокальной плоскости объектива наблюдаются дифракционные изображения звезд (рис. 3.9.3).
Дифракционные изображения двух близких звезд в фокальной плоскости объектива телескопа
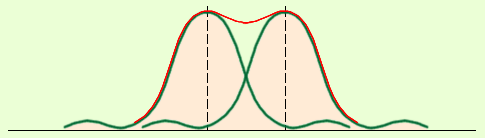
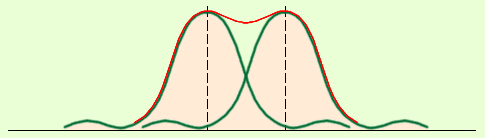
На рис. 3.9.3 расстояние Δl между центрами дифракционных изображений звезд превышает радиус r центрального светлого пятна – в этом случае изображения звезд воспринимаются наблюдателем раздельно и, следовательно, объектив телескопа позволяет разрешить две близкие звезды. При уменьшении углового расстояния ψ между звездами дифракционные изображения могут сильно перекрыться и перестанут отличаться от изображения одиночной звезды. В этом случае объектив телескопа не разрешает близкие звезды. Английский физик Дж. Релей в конце XIX в. предложил условно считать разрешение полным, когда расстояния Δl между центрами изображений равно (или превышает) радиус r диска Эйри (рис. 3.9.4). Условие Δl = r называют критерием разрешения Релея. Из этого критерия следует:
Телескоп с диаметром объектива D = 1 м способен разрешать две звезды, находящиеся на угловом расстоянии ψmin = 6,7·10–7 рад (для λ = 550 нм).
Рисунок 3.9.4. Предел разрешения по Релею. Красная кривая – распределение суммарной интенсивности света
Космический телескоп Хаббла, выведенный на орбиту в 1990 году, имеет зеркало диаметром D = 2,40 м. Предельное угловое разрешение этого телескопа на длине волны λ = 550 нм равно: ψmin = 2,8·10–7 рад. На работу космического телескопа не оказывают влияния атмосферные возмущения. Для характеристики объектива телескопа можно ввести величину R, обратную предельному углу ψmin. Эту величину называют разрешающей силой телескопа:
Для увеличения разрешающей способности телескопа следует увеличивать диаметр объектива (либо переходить к более коротким волнам). Все сказанное выше о разрешающей способности телескопа применимо и к невооруженному глазу. Глаз при рассматривании удаленных предметов действует так же, как и объектив телескопа. Роль D играет диаметр зрачка глаза dзр. Полагая dзр = 3 мм, λ = 550 нм, найдем для предельного углового разрешения глаза
Этот результат хорошо согласуется с физиологической оценкой разрешающей способности глаза, выполненной исходя из размеров светочувствительных элементов сетчатки (палочек и колбочек).
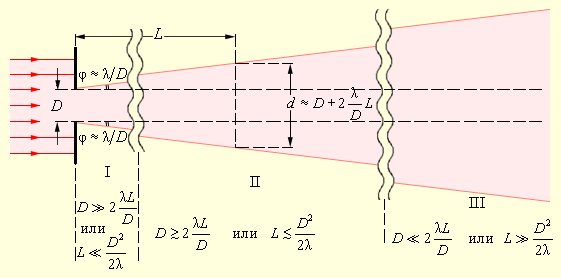
Теперь можно сделать один общий вывод: световой пучок с диаметром D и длиной волны λ вследствие волновой природы света испытывает дифракционное уширение. Угловая полуширина φ пучка оказывается порядка λ / D, так что полная ширина d пучка на расстоянии L приблизительно равна
Рис. 3.9.5 качественно показывает, как по мере удаления от препятствия трансформируется пучок света.
Рисунок 3.9.5. Пучок света, расширяющийся вследствие дифракции. Область I – понятие луча света, законы геометрической оптики. Область II – зоны Френеля, пятно Пуассона. Область III – дифракция в параллельных лучах
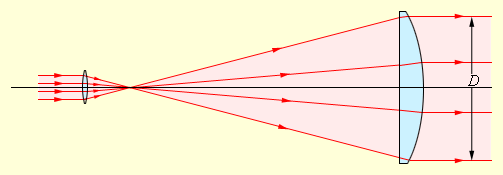
Оценки, выполненные на рис. 3.9.5, показывают, что угловое расхождение пучка уменьшается при увеличении его первоначального поперечного размера D. Этот вывод справедлив для волн любой физической природы. Чтобы, например, послать «узкий» пучок лазерного излучения на Луну, нужно сначала его расширить. Это достигается с помощью телескопа: лазерный пучок направляется в окуляр и затем, пройдя через телескоп, выходит из объектива, имея диаметр D (рис. 3.9.6).
Рисунок 3.9.6. Расширение лазерного пучка с помощью телескопической системы
Такой расширенный пучок, дойдя до Луны, «засветит» на ее поверхности пятно радиусом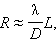 
где L – расстояние до
Луны. Приняв D = 2,5 м (телескоп-рефлектор Крымской обсерватории), λ = 550 нм, L = 4·106 м, получим R ≈ 90 м. Если бы на Луну был направлен первоначальный пучок лазерного света, имеющий диаметр порядка 1 см, то он «засветил» бы на Луне пятно, радиус которого оказался бы в 250 раз больше.
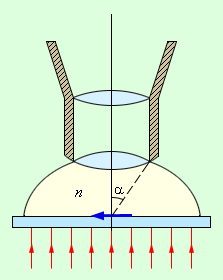
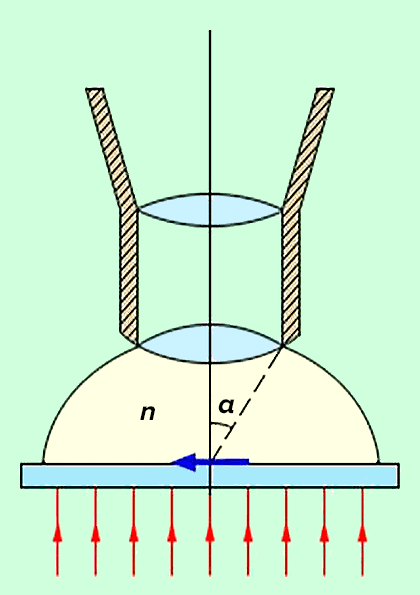
Разрешающая способность микроскопа. С помощью микроскопа наблюдают близко расположенные объекты, поэтому его разрешающая способность характеризуется не угловым, а линейным расстоянием между двумя близкими точками, которые еще могут восприниматься раздельно. Наблюдаемый объект располагается вблизи переднего фокуса объектива. Часто пространство перед объективом заполняется специальной прозрачной жидкостью – иммерсией (рис. 3.9.7). В плоскости, геометрически сопряженной объекту, располагается его увеличенное изображение, которое рассматривается глазом через окуляр. Изображение каждой точки оказывается размытым вследствие дифракции света.
Рисунок 3.9.7. Иммерсионная жидкость перед объективом микроскопа
Впервые предел разрешения объектива микроскопа был определен в 1874 г. немецким физиком Г. Гельмгольцем. Формула Гельмгольца имеет вид:
Здесь λ – длина волны, n – показатель преломления иммерсионной жидкости, α – так называемый апертурный угол (рис. 3.9.7). Величина n sin α называется числовой апертурой.
У хороших микроскопов апертурный угол α близок к своему пределу: α ≈ π / 2. Как видно из формулы Гельмгольца, применение иммерсии несколько улучшает предел разрешения. Полагая для оценок sin α ≈ 1, n ≈ 1,5, получим:
Таким образом, с помощью микроскопа принципиально невозможно рассмотреть какие-либо детали, размер которых значительно меньше длины волны света. Волновые свойства света определяют предел качества изображения объекта, полученного с помощью любой оптической системы.
Модель. Дифракционный предел разрешения
Пределы разрешения и круговые апертуры
Физика > Пределы разрешения и круговые апертуры
Читайте о дифракционном пределе разрешения и эффекте дифракции: предел Аббе для разрешения микроскопа, как улучшить разрешение объектива, формула.
В оптическом изображении фундаментальная граница разрешения обусловливается дифракцией.
Основные пункты
Термины
Оптическая система, нацеленная на формирование изображения, обладает максимумом для показателя разрешения, что обусловлено дифракцией.
У телескопов с круговыми апертурами наименьшей функцией будет размер диска Эйри. Если апертура в линзе уменьшается, то дифракция увеличивается. Вы заметите это, так как кольца от дифракции становятся более отчетливыми. Точно также, если объекты с изображениями уменьшаются, то объекты из дифракции размывают границы.
Дифракционные эффекты наиболее ярко проявляют себя для волн, чья длина практически сходится с размерами дифрагующих объектов. Длина волны пучка образа накладывает фундаментальное ограничение на разрешение в любой оптической системе.
Компьютерное изображение диска Эйри. Интенсивность серой шкалы скорректировали, чтобы увеличить яркость внешних колец диаграммы
Дифракционный предел Аббе для микроскопа
В микроскоп очень сложно наблюдать за субволновыми структурами из-за дифракционного предала Аббе. В 1873 году выяснилось, что свет, перемещающийся в среде не может свестись к пятну с радиусом меньше, чем:
Улучшение разрешения
Если вам нужно увеличить разрешение, то можно использовать более короткие длины волн, вроде УФ и рентгеновские микроскопы. Однако при лучшем разрешении они слишком дорогие и обладают недостатком контраста в биологических образцах (могут повредить их). Остальные способы также упираются в высокую стоимость или сложность осуществления. Как правило, к ним обращаются, если необходимо решить подмножество проблем с изображением.
Лучше один раз увидеть, или Микроскопия сверхвысокого разрешения
Виментин и клатрин, меченные флуоресцентными антителами. Изображение слева получено с помощью традиционного конфокального микроскопа, справа — с применением STED-технологии. С помощью методов сверхвысокого разрешения можно различить структуры до 10 нм (так, справа различимы фибриллы отдельных промежуточных филаментов).
Автор
Редакторы
Статья на конкурс «био/мол/текст»: Благодаря зрению мы получаем 90% информации об окружающем нас мире. Именно поэтому микроскопия играет огромную роль в различных направлениях современной биологии. Долгое время дифракционный барьер не позволял изучать структуры менее 200 нм, но сейчас удалось найти сразу несколько решений данной проблемы.
Конкурс «био/мол/текст»-2012
Эта статья представлена на конкурс научно-популярных работ «био/мол/текст»-2012 в номинации «Лучший обзор».
Спонсор конкурса — дальновидная компания Thermo Fisher Scientific.
Разрешение стандартного оптического микроскопа
Уже с конца XVI века ученые начали применять увеличительные стекла и конструировать первые микроскопы (Ханс Янсен, Галилео Галилей, Корнелиус Дреббель, Кристиан Гюйгенс, Роберт Гук и Антони ван Левенгук), чтобы как можно более подробно изучить тончайшую структуру жизни. Постоянное совершенствование оптических микроскопов привело к тому, что на сегодня достигнуто увеличение более чем в 2000 раз [1]. Можно было бы и еще больше, но дальнейшее увеличение просто не имеет смысла, поскольку оно не поможет различить более мелкие детали препарата.
Поясним, что не следует путать увеличение микроскопа и его разрешающую способность. Так, увеличение определяет, во сколько раз изображение, построенное оптической системой микроскопа, больше самого объекта, а разрешающая способность определяет то минимальное расстояние, на котором независимые источники света будут различимы. Разрешающая способность микроскопа, как было установлено в 1873 году Эрнстом Аббе, характеризуется неким предельным значением, обусловленным волновой природой света. Свет от точечного источника (размеры которого значительно меньше длины световой волны), проходя через оптическую систему, формирует не точку, а светлый кружок с темными и светлыми кольцами (дифракция Фраунгофера или дифракция в параллельных лучах). Функция, характеризующая трехмерное распределение интенсивности света в таком изображении, называется функцией рассеяния точки. На центральный кружок (диск Эйри) приходится 85% интенсивности света, и именно из таких кружков складывается изображение в оптической микроскопии (рис. 1а).
Если два точечных источника света расположены ближе некоторого критического значения, то их изображения (диски Эйри) будут перекрываться, и их невозможно идентифицировать как отдельные светящиеся точки (рис. 1б) [2], [3]. Это минимальное расстояние и есть дифракционный предел, который рассчитывается по формуле d = 0,61λ/NA, где NA = nsinα — нумерическая апертура объектива, n — коэффициент преломления среды, α — угол между оптической осью объектива и наиболее отклоняющимся лучом, попадающим в объектив (апертурный угол), λ — длина световой волны (рис. 1в). В связи с тем, что объект освещается только с одной стороны, разрешение вдоль оптической оси еще меньше: d = 2λn/(NA) 2 [4], [5]. В микроскопии в видимом свете с масляной иммерсией и NA = 1,4 можно достичь максимального разрешения около 200 нм в латеральной плоскости и 500 нм — в аксиальной [6].
Рисунок 1. Дифракционный предел. а — Изображение точечного источника света, сформированное оптической системой микроскопа. На центральный максимум приходится приблизительно 85% интенсивности от всех частей изображения. б — Точечные источники света, расположенные на различном расстоянии друг от друга. Расстояние между источниками 1 и 2 значительно больше d (дифракционного предела). Расстояние между 3 и 4 равно d/2, а между 5 и 6 значительно меньше d/2. в — Изображения двух точечных источников света, полученные объективами с одинаковыми числовыми апертурами (то есть, с одинаковым разрешением), но дающие различное увеличение. Расстояние между источниками составляет d/2. Очевидно, что дополнительное увеличение не позволяет получить более четкую картину.
Технические хитрости
Рисунок 2. Основные параметры, определяющие разрешение объектива: n — коэффициент преломления иммерсионной жидкости и α — апертурный угол объектива.
Очевидно, что такого разрешения недостаточно для детального изучения структуры и процессов, происходящих на субклеточном уровне. Так, например, размеры рибосом, ядерных пор, АТФ-синтаз, клеточных филаментов, микротрубочек и других надмолекулярных структур не превышают 150 нм. Толщина биологических мембран составляет не более 10 нм. Электронная микроскопия позволяет достигнуть необходимого разрешения, но она не пригодна для работы с живыми клетками из-за высокой разрушающей и ионизационной способности, а также предполагает напыление тонких слоев металла или углерода, что может изменить исходные свойства объекта. Атомно-силовая микроскопия «близорука» и не позволяет проникнуть вглубь объекта более чем на 10–20 нм.
Взамен атомно-силовая микроскопия, конечно, обладает другими уникальными свойствами: «Атомно-силовая микроскопия: увидеть, прикоснувшись» [15]. — Ред.
Важной особенностью живых клеток и тканей является низкий контраст внутренних структур, которые в основном прозрачны. Для их идентификации необходимо специфическое окрашивание, в том числе с применением различных флуорофоров (органических молекул, флуоресцентных белков или квантовых точек). Таким образом, флуоресцентная микроскопия сочетает в себе сразу несколько преимуществ. Во-первых, возможность прижизненного изучения объектов и наблюдения процессов в реальном времени. Во-вторых, возможность специфического мечения тканей, клеток, органелл и отдельных молекул. В-третьих, доступное на данный момент разнообразие флуоресцентных красителей и белков позволяет изучать одновременно несколько мишеней [6].
Общая концепция применения флуоресцентных методов в молекулярно-биологических исследованиях изложена в статье «Рулетка для спектроскописта» [16]. На сайте Института биоорганической химии РАН можно посмотреть видеозаписи трех докладов, объединенных общей темой «Флуорофоры: органические, неорганические и генетически кодируемые». — Ред.
Существует достаточно много технологий, основанных на различных физических феноменах, позволяющих увеличить разрешение как в латеральном, так и аксиальном направлениях. Ближнепольная сканирующая микроскопия (микроскопия без использования линз) преодолевает дифракционный предел (разрешение порядка 20–50 нм), но позволяет изучать только поверхностные свойства объекта [6]. Однако биологические объекты трехмерны, и с увеличением толщины объекта свет от разных слоев будет затруднять интерпретацию изображения конкретного оптического среза. Известно несколько методов микроскопии дальнего поля, значимость которых в первую очередь определяется заметным улучшением разрешения вдоль оси Z.
В конфокальном микроскопе применяется апертура в фокальной плоскости объектива, пропускающая свет только от объектов, находящихся в фокусе [7]. Мультифотонная микроскопия основана на возможности двухфотонного или трехфотонного возбуждения флуоресценции. Например, флуорофор, обычно поглощающий ультрафиолетовое излучение (≈350 нм), может быть возбужден двумя красными фотонами (≈700 нм), если они достигли флуорофора одновременно (поглощение будет зависеть от квадрата интенсивности возбуждающего излучения). Это значит, что необходима высокая плотность фотонов для возбуждения флуоресценции. Достаточная плотность достигается в фокусе, поэтому возбуждение флуоресценции происходит только в фокальной плоскости [8]. В I 5 M- и 4Pi-микроскопии применяются два объектива для возбуждения и/или регистрации флуоресценции, что позволяет освещать и регистрировать флуоресценцию с двух сторон от образца и заметно увеличить разрешение вдоль оптической оси (до 100 нм) [6].
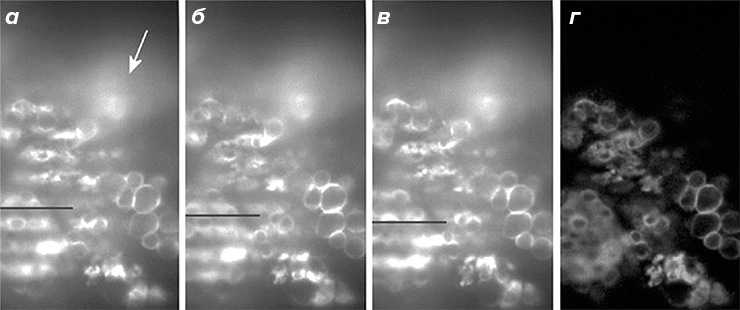
Еще одним интересным методом является микроскопия структурированного освещения — SIM (Structured Illumination Microscopy). В плоскости, сопряженной с фокальной, располагается решетка, создающая определенный паттерн освещения. Индуцируемая флуоресценция повторяет паттерн освещения, при этом флуоресценция объектов, расположенных в фокальной плоскости, сильно меняется при перемещении этого паттерна. Флуоресценция объектов, расположенных не в фокусе, от сдвига решетки практически не зависит. Последующая компьютерная обработка позволяет отсечь флуоресценцию от остальных оптических слоев и также улучшить разрешение вдоль оси Z (рис. 3). В HR-SIM (High Resolution SIM) на образец проецируется освещение, характеризующееся высокой периодичностью. При взаимодействии с неизвестной структурой объекта, получается изображение с периодом выше, чем у двух изначально взаимодействующих образцов решетки и исследуемого объекта (эффект муара). Несколько раз изменяя положение решетки и анализируя различные изображения с муаровым эффектом, можно воссоздать исходную структуру объекта, недоступную обычной микроскопии из-за дифракционного предела [9].
Рисунок 3. Микроскопия структурированного освещения. На трех исходных изображениях (а—в) видно, что при перемещении решетки (обозначено черной линией) интенсивность флуоресценции объектов, расположенных в фокусе, заметно меняется. Флуоресценция, исходящая от других оптических слоев, практически не меняется (обозначено белой стрелкой), что позволяет избавиться от нее за счет компьютерной обработки (г).
Все перечисленные выше методы не преодолевают дифракционный предел как таковой. Сочетая сразу несколько из них, вдоль осей XYZ возможно увеличить разрешение максимум в два раза, но оно по-прежнему будет зависеть от λ и α [4].
Микроскопия сверхвысокого разрешения
Таким образом, из-за дифракции вместо точечного изображения флуорофора получается размытое пятно. Однако дифракция не препятствует более точному определению координат данного флуорофора, если в его окрестности не находятся другие источники флуоресценции. Если флуоресцентные молекулы можно обратимо переводить из флуоресцентного состояния А в темновое состояние В так, чтобы молекулы в состоянии А были окружены молекулами в состоянии В, координаты молекул в состоянии А можно определить достаточно точно. Последовательно регистрируя некоторый пул молекул в состоянии А и запоминая в каждом считывании их координаты, из этих данных можно реконструировать изображение с субдифракционным разрешением [10].
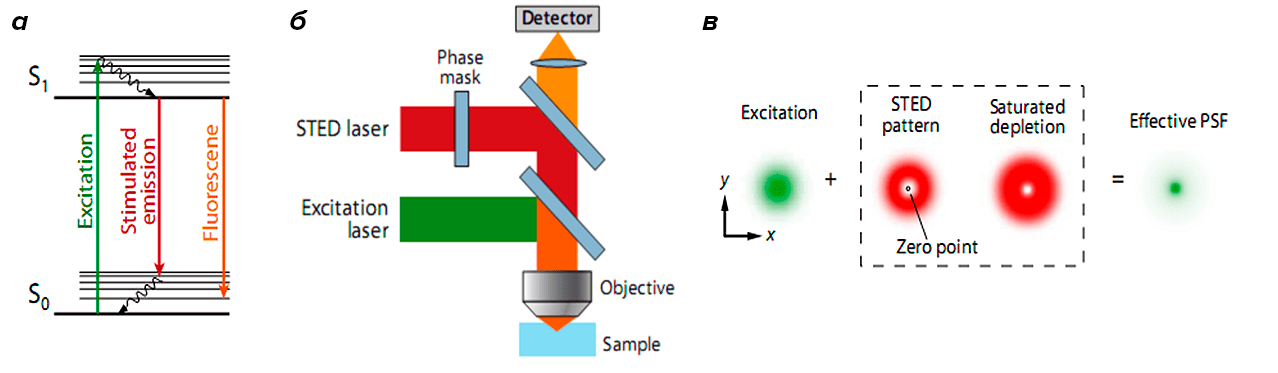
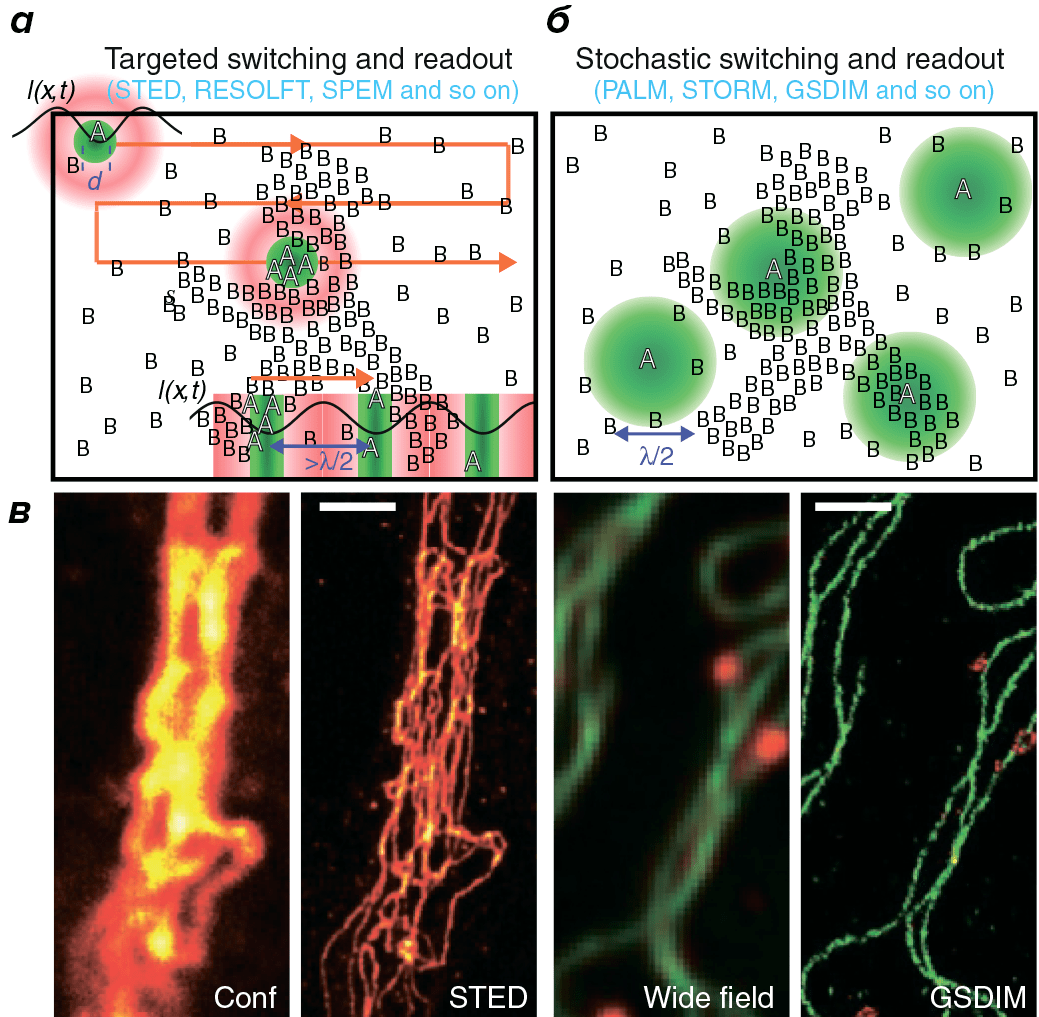
Один из способов определить точное положение флуоресцирующих молекул в некоторой точке — целенаправленно перевести флуорофоры вокруг этой точки в темновое состояние [10]. Данный подход реализован в группе методов RESOLFT (REversible Saturable OpticaL Fluorescence Transitions), объединяющей несколько похожих концепций [4]. Первая практически реализованная из них — это микроскопия STED (STimulated Emission Depletion, метод подавления спонтанного испускания), основанная на подавлении эмиссии флуорофоров, расположенных вне центра возбуждения. Когда флуорофор находится в возбужденном состоянии А и встречает фотон с энергией, соответствующей разнице энергий между возбужденным и основным состоянием В, он возвращается в основное состояние до того, как произойдет спонтанная флуоресценция (рис. 4а). Для вынужденной эмиссии флуорофоры освещаются кроме возбуждающего света STED-лазером с особым пространственным распределением интенсивностей в виде «пончика» с нулевой интенсивностью в центре. В результате флуоресцируют только молекулы, расположенные близко к области с нулевой интенсивностью STED-лазера, что сужает размер функции рассеяния точки (рис. 4б, в). Далее последовательно происходит сканирование всего образца (рис. 5) [4].
О применении STED-микроскопии для изучения субмикроскопических неоднородностей в липидных мембранах клеток и визуализации распределения некоторых мембранных белков между жидкокристаллической и «рафтовой» фазами мембраны мы писали в статье «Липидный фундамент жизни» [17]. — Ред.
Рисунок 4. STED-микроскопия. а — Процесс вынужденной и спонтанной эмиссии. Когда флуорофор поглощает фотон возбуждающего света, он переходит из основного состояния S0 в возбужденное S1. Спонтанная эмиссия происходит, когда флуорофор возвращается в основное состояние. Вынужденная эмиссия происходит, если флуорофор поглощает фотон с энергией, сравнимой с разницей между основным и возбужденным состоянием. б — Схематическое изображение STED-микроскопа: свет от возбуждающего и STED-лазера одновременно фокусируются на одном участке образца. в — Распределение интенсивностей возбуждающего лазера и STED-лазера, который подавляет спонтанную флуоресценцию вокруг нулевой точки. В результате сужается функция рассеяния точки.
Рисунок 5. Две стратегии получения изображений со сверхвысоким разрешением. При направленном считывании данных (а) каждая точка образца облучается светом с особым распределением интенсивностей, так что все молекулы вокруг данной точки оказываются в темновом состоянии. Это уменьшает размеры участка с молекулами во флуоресцентном состоянии и, следовательно, функцию рассеяния точки. Для увеличения скорости сканирования образца можно применить распределение интенсивностей в виде линий с максимумами и нулевыми значениями (правый нижний угол). Для высокого разрешения по всем направлениям необходимо несколько раз повернуть паттерн освещения. При стохастическом считывании данных (б) индивидуальные молекулы переключаются между флуоресцентным и темновым состоянием. Интенсивность возбуждающего света подобрана так, что флуоресцирующие молекулы окружены молекулами в темновом состоянии. Если флуорофор яркий, можно очень точно определить его локализацию. в — Сравнение изображений, полученных с помощью оптической микроскопии и технологий сверхвысокого разрешения: слева — меченный антителами виментин, справа — микротрубочки (зеленые) и пероксисомы (красные) в клетках млекопитающих.
Метод STED позволят получить субдифракционное разрешение, рассчитываемое по формуле
где Imax — применяемая интенсивность STED-лазера, Isat — интенсивность, которая необходима для 50% вынужденной эмиссии. Увеличение Imax до высоких значений способствует быстрому фотовыцветанию образца, поэтому для увеличения разрешения можно уменьшить Isat, которая обратно пропорциональна времени жизни флуорофора. Для этого можно изменить природу флуоресцентного состояния А и темнового В [11]. В методе STED S0 — основное, а S1 — возбужденное флуоресцентное состояние. В других методах переход из флуоресцентого состояния в темновое может представлять фотохимическую реакцию с цис—транс изомеризацией хромофора флуоресцентного белка или переход между флуоресцентным и триплетным состояниями флуорофора [10].
Принципиально другой подход основан на последовательной стохастической активации флуорофоров. Если за каждый раунд активации небольшое число флуорофоров переходит в флуоресцентное состояние А, и при этом интенсивность света подобрана таким образом, что активированные флуорофоры находятся на расстоянии примерно 200 нм, то положение каждого флуорофора можно определить с точностью до 1 нм. Далее активированные флуорофоры «выключают».
Многократное повторение циклов активации позволяет реконструировать изображении со сверхвысоким разрешением (рис. 5), где х — точность локализации (параметр, соответствующий разрешению в традиционной микроскопии), k1 и k2 определяются длиной волны возбуждаемого света, нумерической апертурой объектива и размерами пикселя, b — уровень шума на пиксель и N — число испущенных фотонов. Исходя из формулы, для данного типа микроскопии предпочтительны яркие флуорофоры с высоким коэффициентом экстинкции и квантовым выходом [11].
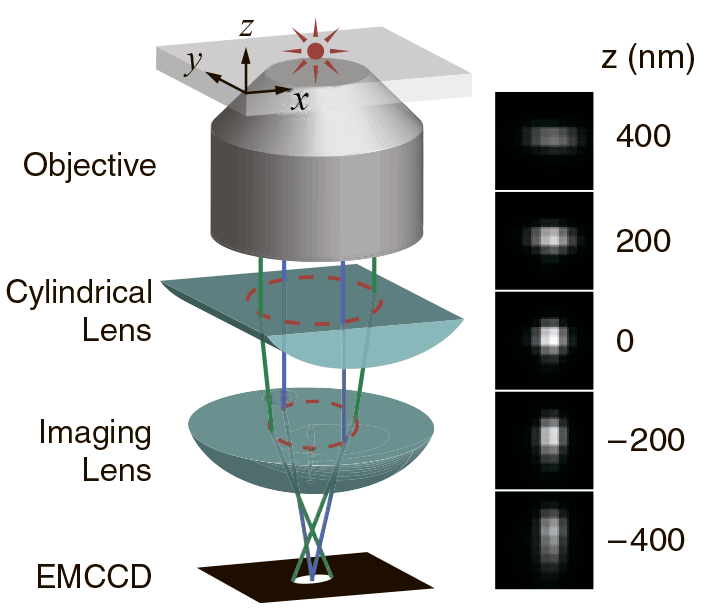
При изучении 3D-структуры биологических объектов для построения изображения применяют слабые цилиндрические линзы. У таких линз фокальные плоскости в направлениях X и Y немного отличаются. Таким образом, эллиптичность и ориентация изображения флуорофора зависит от его положения по оси Z. Когда флуорофор находится в средней фокальной плоскости (примерно посередине между фокальными плоскостями для латеральных направлений X и Y), то функция рассеяния точки изодиаметрична (имеет одинаковую длину по осям X и Y). Когда флуорофор расположен выше фокальной плоскости, изображение более сфокусировано вдоль оси Y, чем оси X, поэтому оно выглядит не круглым, как в предыдущем случае, а овальным (вытянутым вдоль оси X). И наоборот, когда флуорофор находится ниже средней фокальной плоскости, функция рассеяния точки оказывается вытянутой вдоль оси Y. Анализируя форму полученных изображений, можно установить не только координаты флуорофора по осям X и Y, но и однозначно определить положение относительно оси Z (рис. 6) [13].
Рисунок 6. Принцип микроскопии 3D-STORM. Трехмерная локализация индивидуальных флуорофоров с использованием цилиндрических линз. На диаграмме справа показано, как связаны эллиптичность изображения флуорофора и его Z-координата.
Дифракционный предел преодолен!
И, наконец, необходимо сказать, что недавно физики открыли способ непосредственно преодолеть дифракционный предел. Для этого необходимо сконструировать микроскоп с линзами из метаматериала — материала с отрицательным коэффициентом преломления. Веществ с такими свойствами в природе не обнаружено, их можно получить только искусственным путем в лаборатории. Существование таких веществ было предсказано еще 40 лет назад советским физиком Виктором Веселаго, а созданы они были только в 2000-х годах. Так, отрицательный коэффициент преломления означает, что преломленный луч в среде с отрицательным коэффициентом находится с той же стороны, что и падающий (обычно падающий и преломленный лучи находятся с разных сторон от нормали, поведенной к границе раздела сред). Поэтому плоский брусок такого материала может выполнять роль суперлинзы, позволяющей различить детали по размерам меньшие полудлины волны [14].