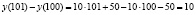Что такое предельные величины в экономике
Предельные величины
Предельная (маржинальная, от фр. marginal — находящийся на краю чего-либо) величина — это прирост одной величины, вызванный приростом другой величины на единицу (при условии, что все остальные величины остаются неизменными). [1] Предельные величины — это наличие в экономике приростных процессов, малых изменений, которые чрезвычайно распространены и весьма разнохарактерны. С их помощью устанавливается ограничения приростных процессов с позиции производителя, продавца или покупателя. Они имеют отношение к теории равновесия.
Содержание
[править] Предельная полезность
Предельная полезность — добавочная польза потребителя от применения дополнительной единицы блага. Теория предельной полезности опирается на положение, согласно которому полезность использования каждой последующей единицы продукта снижается после некоторого значения, соответствующего наивысшей степени удовлетворённости им, хотя совокупная полезность возрастает. Предельная полезность рассматривается как одна из фундаментальных категорий, на основе которой формируются теории потребительского спроса, хозяйственного поведения фирм и индивидов.
Закон убывающей предельной полезности — это экономический закон, который гласит, что по мере того, как потребитель увеличивает потребление товара или услуги, предельная полезность каждой дополнительной единицы данного продукта сокращается. Согласно этому закону производители должны понижать цену для того, чтобы побуждать потребителей к увеличению покупок такого продукта. Это объясняет, почему кривая спроса на такие блага имеет отрицательный наклон. Этот закон был открыт в 1854 году немецким экономистом Германом Генрихом Госсеном. Этот закон легко и естественно объясняет закон спроса. Поскольку ценность новых единиц блага для потребителя падает, он готов приобретать все больше и больше экземпляров товара только при условии снижения их цены.
[править] Предельные издержки
Предельные издержки-добавочные затраты при малых изменениях объёма производства. Каждый данный момент состояния производства независимые от объёма выпуска постоянные затраты представляют собой в целом величину определённую. Тогда любой дополнительный прирост продукции связан преимущественно с переменными издержками, поэтому от постоянных издержек в предельном анализе отвлекаются.
Что такое предельные величины в экономике
Сторонники неоклассического направления широко применяют математические методы в экономической теории. Они приспособили дифференциальное исчисление к анализу предельных величин в экономике. На базе чистой экономики они пытались вывести так называемые естественные законы, определяющие стоимость и цены, прибыль и заработную плату, а также законы распределения доходов. [c.47]
Новое, близкое и уже хорошо знакомое нам звучание получила трактовка распределения с появлением учения о предельных величинах в экономике. Маржиналисты, как правило, не строили отдель- [c.208]
Обосновать «кривизну» кривых спроса и предложения двумя факторами ролью предельных величин в экономике и фактором времени. [c.164]
Что такое предельная величина Приведите примеры предельных величин в экономике. Каково различие в определениях средней величины в дискретном и в непрерывном случаях Приведите практические примеры. [c.100]
Предельные (добавочные, дополнительные, маржинальные) величины показывают характер и скорость изменения средни удельных величин исследуемых показателей. Их рассчитывают как разность предыдущих и последующих средних удельных величин, связанных с производством добавочной единицы продукции В итоге маржинальный анализ позволяет установить, как изменяется средний уровень удельных показателей при увеличении (снижении) объема производства продукции на единицу. Предельные величины в экономике начали исследоваться со второй половины XIX в., когда возникла новая школа — маржинализм. В настоящее время вся экономическая наука западных стран строится на предельных и критических величинах объемов продаж, себестоимости, прибыли, цены, постоянных затрат и их оптимизации. [c.196]
Предельные и приростные величины в экономике [c.276]
Дифференциальное исчисление в форме П.а. применяется в экономике, в частности при решении задач оптимального программирования, а также в моделях теории экономического роста и др. На выводах П.а. основаны ряд важнейших положений современной экономической науки, напр. необходимость равенства предельной нормы замещения конкурирующих благ, производственных факторов и т.п. для получения максимального результата. Надо учесть, однако, что экономика не всегда позволяет использовать предельные величины в силу неделимости многих объектов экономических расчетов. Кроме того, применению предельных величин препятствует прерывность (дискретность) экономических показателей во времени в большинстве случаев в практическом моделировании приходится пользоваться годовыми (реже месячными и т.д.) показателями. Но все же нередко, особенно в теоретических исследованиях, когда оказывается возможным отвлечься от дискретности, П.а. является полезным инструментом экономической науки. [c.277]
Средние величины широко используются для обобщенных характеристик всевозможных массовых процессов, в том числе и в экономике. С их помощью устраняются индивидуальные различия, выявляются общие условия и закономерности, осуществляются расчеты по прогнозированию и планированию, анализ экономических явлений (рис. П.5 к ст. «Предельные и приростные величины в экономике»). Наиболее часто применяются средняя арифметическая (невзвешенная) [c.341]
Дифференциальное исчисление в форме предельного анализа широко применяется в экономике, в.частности при решении задач оптимального программирования, а также в моделях экономического роста и др. Экономика не всегда позволяет использовать предельные величины в силу неделимости многих крупных объектов экономических расчетов. Но в ряде случаев предельный анализ выступает как важный математический инструмент экономической науки. [c.24]
Встречаясь с этими величинами в экономике, часто приходится использовать соотношения между ними (например, между суммарными, средними и предельными издержками) и решать задачи на нахождение по одной из этих величин двух других (например, среднего и предельного дохода по суммарному доходу). [c.91]
Условие, приведенное в уравнении (3.3), представляет собой пример определенного рода условий оптимальности в экономике. В данном примере максимизация достигается, когда предельная выгода, т. е. выгода, связанная с потреблением одной дополнительной единицы продовольствия, равна предельным (маржинальным) издержкам. Предельная выгода измеряется MRS. В точке А она равняется /2 (в этой точке на бюджетной линии PF= 1 и Рс =2), что означает, что потребитель должен отказаться от /2 единицы одежды, чтобы получить 1 единицу продуктов питания. В этой же точке предельные издержки измеряются величиной углового коэффициента бюджетной линии, она также равна /2> потому что затраты на приобретение одной единицы продовольствия окупаются при отказе от затрат на /2 единицы одежды. [c.85]
Если цель правительства — максимизировать доход от эмиссии денег, то оно выпускает такое количество монет, чтобы предельный доход был равен предельным издержкам выпуска последней монеты, что соответствует объему выпуска
Что такое предельные величины в экономике
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции получать новую функцию, которую называют производной функцией (или просто производной) данной функции, процесс получения новой функции был назван дифференцированием.
Использование производной применяется во многих науках, но в данной статье хотелось бы осветить использование производной в сфере экономики.
В экономической теории активно используется понятие «маржинальный» или «предельный». Следует отметить, что маржинализм – направление, возникшее в XIX веке в экономической науке, признающее высокую роль предельных (маржинальных) величин в науке, речь о которых пойдёт далее.
Важный раздел методов дифференциального исчисления, используемых в экономике – методы предельного анализа, то есть совокупность приемов исследования изменяющихся величин затрат или результатов при изменениях объемов производства, потребления и т. п. на основе анализа их предельных значений.
Теоретический анализ разнообразных явлений экономики использует ряд предельных величин. Перечислим лишь некоторые из них: предельная стоимость, предельные издержки, предельный доход, предельная производительность, предельная полезность, предельная склонность к потреблению. Все эти величины самым тесным образом связаны с понятием производной.
Таким образом, предельный показатель (показатели) функции – это ее производная. Как говорилось выше, в экономике часто используются средние величины, но требуется узнать, на какую величину вырастет результат, если будут увеличены затраты или наоборот, насколько уменьшится результат, если затраты сократятся. С помощью средних величин ответ на этот вопрос получить невозможно. В подобных задачах требуется определить предел отношения приростов результата и затрат, то есть найти предельный эффект.
Следовательно, для их решения необходимо применение методов дифференциального исчисления.
В качестве характерного примера рассмотрим предельные издержки. Следует заметить, что предельные издержки – это затраты, связанные с выпуском одной дополнительной единицы продукции. Пусть y(x) затраты на изготовление х экземпляров некоторого продукта. Тогда y'(x) выражает скорость изменения затрат при изменении количества продукта. Эта производная называется предельной (маржинальной) стоимостью.
Согласно определению производной имеем:
.
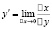
Следовательно, можно считать, что производная y'(x) приближенно равна отношению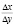 
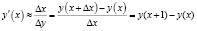
. Пусть ∆x=1. На практике обычно х – очень большое число, так что единица мала по сравнению с х. Откуда:
.
Разность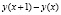 
выражает на сколько изменились затраты (издержки) при изготовлении ещё одного экземпляра продукции, поэтому экономисты определяют предельные издержки y'(x) так же, как и затраты на изготовление одного экземпляра продукции.
Приведём пример. Пусть зависимость между издержками продукции «у» и объемом выпускаемой продукции «х» на предприятии выражается функцией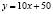 
. Определим предельные издержки при объеме продукции x=100 единиц.
Поскольку предельные издержки выражаются производной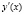 
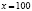
, при 
предельные издержки составят y'(100)=10. Это означает, что при данном уровне производства (количестве выпущенной продукции 100 единиц) на выпуск единицы дополнительной продукции необходимы дополнительные затраты в 10 денежных единиц. Действительно, затраты на выпуск сто первой единицы продукции можно подсчитать и по другому:
Для нашего примера (в случае, когда «у» является линейной функцией от переменной х) разность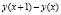 
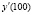
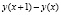
совпадает со значением производной 
. В общем же случае (когда функция y(x) может быть нелинейной) при больших «х» разность 
совпадает с y'(x) лишь приближенно.
Как видно, предельная величина характеризует не состояние (как суммарная или средняя величина), а процесс (как изменение экономического объекта). Таким образом, предельная величина выступает как скорость изменения некоторого экономического объекта (процесса).
Помимо предельных издержек с помощью производной могут быть определены: предельных доход, предельная стоимость, предельный спрос, предельная выручка, предельная производительность труда и другие предельные величины.
Понятно, что использование этих методов имеет немаловажную роль в решении экономических задач различного характера.
Определение предельных величин с помощью понятия производной позволяет использовать математический аппарат для доказательства экономических законов.
Приведём яркий пример применения дифференциального исчисления в экономической теории.
Пусть «х» – количество реализованного товара, R(х) – функция дохода, С(х) – функция издержек (затрат на производство товара). Вид этих функций зависит от способа производства, оптимизации, инфраструктуры и т.п. Обозначим функцию прибыли как P(x). Тогда:
.
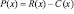
Очевидно, оптимальным уровнем производства является тот, при котором прибыль максимальна, то есть такое значение выпуска «х», при котором функция Р(х) имеет максимум. Следовательно, в этой точке:
.
Но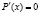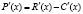 
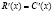
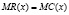
. Поэтому 
, то есть если уровень выпуска продукции «х» является оптимальным для производителя, то:
,
где MR(x) – предельный доход; MC(x) – предельные издержки.
Благодаря применению производных, мы получили известное в экономической науке утверждение «Для того, чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны», – что подтверждает, важность использования математического аппарата для доказательства экономических законов.
Таким образом, применение математических методов в экономике не ограничивается применением производных, осуществленным в идеях маржиналистов, а очень широко распространено и постоянно развивается и совершенствуется.
Теория предельных величин: сущность, измерение и практическое объяснение
Экономические науки
Похожие материалы
В экономической теории активно используется понятие «маржинальный» или «предельный». Следует отметить, что маржинализм – направление, возникшее в XIX веке в экономической науке, признающее высокую роль предельных (маржинальных) величин в науке, речь о которых пойдёт далее.
Неоклассическое направление возникло в результате маржинальной революции, когда в экономике начинает использоваться маржинальний (предельный) анализ [4]. Классическое направление политэкономии не изучало поведения субъектов на рынке и потому не создало целостного учения о рыночной системе ведения хозяйства. Этим занялась австрийская школа (70-90гг. 19ст.) политэкономии, основатель – Карл Менгер, представители: Бем-Баверк и Визер. Они выдвинули субъективно-психологическую концепцию ценности и противопоставили ее трудовой теории стоимости. Ценность блага определяется субъективной оценкой полезности индивидом последней единицы блага, которая удовлетворяет наименее значащую потребность [1].
Основоположником американской школы был Джон Кларк. Он ввел понятие «предельная производительность», разрабатывал теорию производства [1].
Можно вывести следующие аспекты маржинализма:
Первый этап. На этой стадии понятие стоимости сохранялось в качестве исходной категории. Однако при этом была изменена сама ее теория. Стоимость определялась не по трудовым затратам, а по предельной полезности продукции.
Таким образом, теория маржинализма обусловила включение в анализ проблем устойчивого состояния и проблем равновесия. В рамках направления широко применяются математические методы, в числе которых и дифференциальные вычисления. Они используются не только в анализе предельных показателей, но и для обоснования тех или иных решений в процессе выбора их возможного количества состояний наилучший вариант.
Менгер, являвшийся основоположником австрийской концепции экономического анализа, соединил систему предельных понятий с хозяйственным либерализмом. В качестве исходного пункта выступают потребности, которые существуют у людей. События или предметы, которые удовлетворяют нужды человека, именуются благами. Самыми насущными считаются потребительские вещи или явления. Для их производства используются блага второго и следующих порядков. За счет этого ресурсы, идущие на изготовление продукции, наделяются ценностью.
Полезностью считается характеристика, которую человек приписывает благам с учетом соотношения между объемом их предложения и уровнем удовлетворения нужд. В этой связи каждая новая единица продукта получает меньшую ценность. Когда Менгер сформулировал основные идеи на математическом языке, стало ясно, что любая хозяйственная деятельность может сводиться к задаче поиска максимума (выпуска, дохода) либо минимума (расходов) при текущем ограниченном количестве ресурсов.
Концепция Джевонса. Этот экономист сформулировал теорему, которая впоследствии получила его имя. Он вывел следующее: при рациональном потреблении уровень полезности приобретенных продуктов пропорционален их ценам. Джевонс говорил о том, что труд оказывает косвенное влияние на меновые пропорции. Увеличение приложения рабочей силы повышает количество конкретного блага, уменьшая при этом его максимальную полезность. Последнее понятие Джевонс относит к труду не только как к производственному фактору, но и как к процессу. Когда расходы на рабочие ресурсы увеличиваются, деятельность становится тягостной. Она получает отрицательную полезность. И пока она меньше по абсолютному показателю полезности продукта, труд будет осуществляться. При достижении равенства между этими элементами производство блага прекращается.
Второй этап: маржинализм в экономике по Маршаллу. Результатом второй стадии революции стало возникновение неоклассической школы. Приверженцы этой концепции переняли у представителей классической теории приоритет принципов либерализма, предпочтение чистым выводам без психологических, субъективистских и иных наслоений. Маршалл считается самым синтетическим деятелем во всей науке. В его концепции органически соединяются достижения классиков (Милля, Смита, Рикардо) и маржиналистов. Ключевым элементом исследований выступает вопрос свободного ценообразования. Рыночная цена рассматривается Маршаллом как итог пересечения показателя спроса, определяемого максимальной полезностью, и величины предложения, исходящей из предельных издержек.
В своих работах, исследуя маржинализм в экономике, Маршал вывел концепции возрастающей и постоянной отдачи. По первому закону, повышение объема трудовых затрат и капитала приводит к усовершенствованию производства. Это, в свою очередь, увеличивает эффективность деятельности и дает высокую отдачу. В соответствии со вторым законом, увеличение трудовых и прочих издержек приводит к пропорциональному повышению количества продукции. Маршалл считал, что в конкурентных условиях удельные затраты при укрупнении производства или понижаются, или идут параллельно. Но они не опережают темп увеличения объема продукции. Спустя время на базе этих суждений в микроэкономической теории были выдвинуты более достоверные решения вопроса оптимизации производства и размера предприятий. Маршалл в своих исследованиях разделял издержки на переменные и постоянные. Он показал, что в продолжительном периоде последние становятся первыми. Маршалл считал, что в качестве главной причины, по которой фирма уходит с рынка, выступает превышение издержек над уровнем рыночной цены.
Производительность, относящаяся к этому моменту, называется «предельной». При последующем увеличении штата за пределы этой зоны это будет приносить убытки капиталу как производственному фактору. Исходя из этого, Кларк сделал вывод, что размер зарплаты зависит:
Таким образом, чем больше рабочих, тем ниже производительность и, соответственно, меньше оплата. Кроме этого, Кларк говорил о том, что устойчивость состояния общества зависит, в первую очередь, от того, равна ли сумма, которую получают трудящиеся (вне зависимости от величины) тому, что они выпускают. Если рабочие создают небольшую сумму и имеют ее в полном размере, то социальная революция нецелесообразна.
Несовершенная конкуренция. Эта модель базировалась на следующих теоретических предпосылках:
Многие деятели понимали условность этих аспектов. В этой связи к началу 20-го столетия появились труды, авторы которых старались учитывать влияние монополий на рыночную структуру. Так, например, Э. Чемберлин пытался решить следующие задачи:
В рамках научного направления конкуренция и монополия рассматривались как явления, взаимно исключающие друг друга. Конкурентоспособность товара – это его полезность в качестве потребительной стоимости в конкретных условиях[6]. Э. Чемберлин указывал на то, что в действительности существует их синтез. То есть для реального положения дел типична монополистическая конкуренция.
Издержки сбыта. Это понятие Чемберлин использовал вместо производственных затрат. Издержки сбыта, по его мнению, направлены на приспосабливание спроса к продукции. Рыночная структура в рамках монополистической конкуренции определяется за счет трех факторов:
Платой за дифференцированное потребление выступают безработица, недогрузка мощностей производства, повышение цен. Эти факторы не являются следствием недостатка совокупного спроса.
Общественное благо. Его определение осуществляется с использованием двух подходов. Первый позволяет сформулировать концепцию общественно-экономического управления. Она предполагает знание социальной целевой функции и методов ее оптимизации. В качестве одного из способов выступает голосование и принятие решения большинством. Но этот вариант не гарантирует выявления предпочтений в общем случае. Второй подход разработан Парето. Этот ученый основывал свои исследования на утверждении о том, что максимум благосостояния обеспечивается при совершенной конкуренции.
Использование в теории предельных величин привело к возникновению математической школы (Джевонс, Вальрас, Парето) в 30-80гг. 19ст. Они занимались анализом статики и динамики хозяйственной системы, выясняли условия установления рыночного равновесия.
Неоклассическое направление состояло из учений разных школ, и нужно было систематизировать и обобщить их результаты. Это сделал руководитель кафедры экономической теории кембриджского университета проф. А. Маршал (1842-1924 гг.). Он считал, что необходимо отмежеваться от политической экономии, так как этот термин определяет экономику на государственном уровне, и назвал свою основную работу «принципы экономикс».
Основные идеи неоклассической школы [5]:
Кейнсианство (30-70 гг. 20ст.). В 30-х годах вследствие возникновения монополий был подорван рыночный механизм регулирования экономики. „Великая депрессия” отбросила развитые страны на несколько десятилетий назад, привела к появлению новых моделей в экономической теории.
Кейнс предлагает активную государственную политику [3]:
Модель использовалась до 70-х гг. в развитых странах, в дальнейшем она себя исчерпала.
Неоконсерватизм – сохранение старых ценностей на новом этапе. 70-80 гг. 20ст. Кризисы вызваны чрезмерным регулированием экономики (высокие налоги, широкие социальные программы расхолаживают экономику) [2].
Необходимо приватизировать государственный сектор экономики, снизить налоги и уменьшить затраты из бюджета на социальные программы. Рекомендации были использованы Премьер-министром Великобритании Маргарет Тетчер и Президентом США Рональдом Рейганом.
Все современные теории не отвергают необходимости государственного регулирования. Они отличаются лишь границами и методами влияния.
Непосредственным предшественником маржиналистов был германский экономист Г. Госсен, который первым сформулировал законы психологической оценки благ. Смысл его концепции возможно коротко сформулировать так: блага имеют ценность для субъекта только в том случае, когда их число менее необходимой, и эта ценность уменьшается с добавлением любой дополнительной единицы.
В 70-е годы XIX в. эти идеи были дополнены и усовершенствованы при помощи предельного анализа («marginal analysis»), который дал наименование этому течению экономической мысли [2].
Что можно сказать о маржинализме, так это то что является достаточно молодым экономическим течением, возникшее в конце девятнадцатого века, и оно объясняет экономические явления и процессы, базируясь на предельных величинах.
Маржинализм пользуется такими величинами, как предельные издержки, предельная производительность и предельная польза, и к тому же базируется на законах убывания предельной полезности, предельной доходности, предельной производительности и понятия спроса и предложения.
Маржинализм пользуется экономико-математическими методами и базируется на количественном анализе. Причина по которой возник маржинализм, считают важность поиска возможностей, при которых данные сервиса производства рассредоточивались бы с максимум полезным результатом между конкурирующими направлениями использования [4].
Подобная смена парадигмы экономической теории, в свою очередь, возникла и культивировалась, по причине бурного развития промышленности и прикладных наук.
Маржинализм возникновением своим обязан трудам математиков-экономистов. В своих выводах и трудах, они явились предтечей математической школы в научной экономике. В таком виде в настоящее время, маржинализм вобрал в себя ныне и неоклассическую и кейнсианскую экономические концепции, а «экономика прежде всего стала наукой, целью которой изучить взаимосвязи между данными целями и данными ограниченными средствами, имеющими альтернативные возможности использования» [3].
Очень важно учитывать такой фактор, что альтернативная возможность подразумевает применении ресурсов и реализацию времени, для того что бы достичь необходимой, одной цели.
Произошла переоценка устоявшихся почти за двухсотлетнюю историю ценностей «классической школы», это было в конце девятнадцатого века, в экономической литературе этот момент достаточно часто описывают как так называемую «маржинальную революцию».
Существовало несколько ветвей маржинализма: австрийская, британская, швейцарская, американская и др. Всех их объединяло не только лишь разбор и оперирование предельными величинами, но еще и ряд методологических постулатов: неприемлемости идей молодого историчной школы об отсутствии общих экономических законов и ошибочность абстрактно-логического способа исследования; стремление к идеологической нейтральности анализа; трактовка экономических субъектов как однородных и равноправных. Маржиналисты изучали так называемую «чистую экономику». Они поставили перед собою вопрос: какие так называемые внутренние законы определяют образования ценности и цены, и распределение доходов, если представить, что человек руководствуется в собственной деятельности «принципу гедонизма» (что в переводе с греческого обозначает удовольствие), т.е. исходит из стремления к удовлетворения собственного интереса. Отвечая на этот вопрос, маржиналисты открыли так называемые универсальные законы предельной полезности и предельной производительности.
Ни одна из экономических теорий не объясняет всех особенностей экономической реальности. Каждая экономическая теория может только с определенной точностью разъяснять определенные разделы экономической науки. В первую очередь это связано с методами исследований, т.е. теоретическим «инструментарием» определенными предположениями, которые могут быть применены лишь в соответствующих областях науки и применение которых бессмысленно в иных [2].
Под предельной величиной (маржинальной величиной, англ. marginal – находящийся на краю) понимают прирост одной величины, вызванный приростом другой величины на единицу при условии, что все остальные величины остаются неизменными. [1]
Допустим, что в фермерском хозяйстве выращивается пшеница. Отрасль сельского хозяйства является одной из самых рисковых отраслей народного хозяйства. Это связано значительным влиянием природно- климатических факторов, влияющих на производство продукции сельско-хозяйственными товаропроизводителями[8]. Рост применения химических удобрений (при неизменности остальных ресурсов) приводит к увеличению урожая. В расчете на 1 га (табл. 1).
Таблица 1. Рост урожая при росте применения химических удобрений (при неизменности остальных ресурсов) [1]